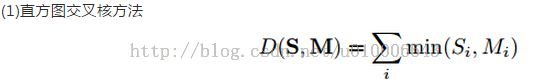人脸识别算法-LBP算法及python实现

上一次我们说了人脸识别算法-特征脸方法（Eigenface）及python实现，在这一次，我们来看一看LBP算法。相比于特征脸方法，LBP的识别率已经有了很大的提升。

在这里，我们用的数据库和上次一样，都是UCI的YALE的人脸数据库。

因为我也是一边学一边写代码，所以害怕有人说我博文是抄袭的，所以在这里说明，我这里的算法思想主要是来自点击打开链接（不过大家都是学习，应该不会这么计较吧），我主要是从实现的角度来说明一下在实现遇见的问题以及方法。

LBP算法介绍：

1.圆形LBP算子

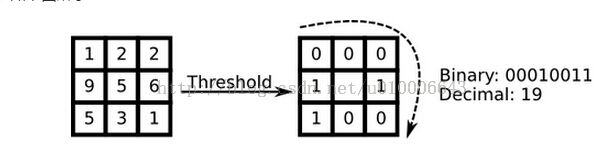
在这个算法一开始的时候，大家使用的是最普通的八邻域算子。

八邻域的像素值大于中心点值的标注1，反之标注0.这样我们就会得到一个八位数。这时我们从左上角开始算最高位，最后左边的为最低位，在这个图中就是00010011，换算十进制就是19，我们就把这个值作为中心点的LBP算子值。

但是随着算法的发展，大家发现这个算子太过死板，不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征，并达到灰度和旋转不变性的要求，Ojala等对 LBP 算子进行了改进，将 3×3邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域。

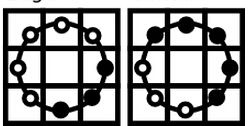
为什么说圆形算子比八邻域算子要更好呢？从直观的角度来说，我们看下面的图

看第一个图是不是很像脸部的右下巴部分，第二图像头部右上方额头？（好吧，如果不像的话，就自己感受一下吧，，个人感觉）

这时我们假设在半径为R的圆形邻域内有P个采样点的算子，上面的图是在R = 2，P=8. 此时我们算每个采样点的坐标：

、

xp 是p点的x坐标，yp是y坐标，p的取值范围（0，P-1）（俗称0,1,2,3,4,5,6,7）。 但此时我们这样得到的不一定是整数，所以可以通过双线性插值来得到该采样点的像素值。（这个双线性插值没太明白，不过python的 scipy工具包里有，我的代码里是直接round函数取整的，大家可以自己加上。）

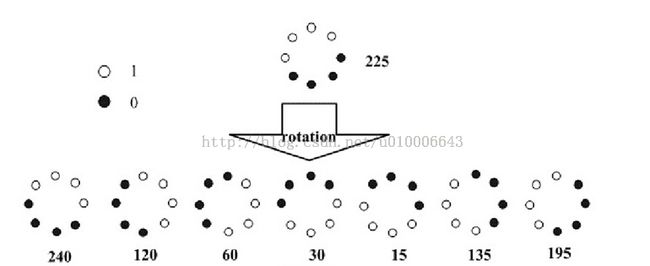
此时我们发现，这个圆形的算子很坑爹啊，万一图片一旋转，同一个点的LBP值就会改变了，很不合理啊，所以大神们用了一种很简单的方法实现了旋转不变性。

如上图所示，原本一开始我们算的这个点的LBP值是11100001 = 225，这时候我们开始旋转，可以看到每一个情况都旋转到了，我们取这些情况中的最小值，也就是15，作为这个点的LBP值，这样不管图片怎么旋转，这个点的LBP值都会是15，也就是旋转不变性。

2.LBP等价模式

这一点的原理是我最没明白的，等到我看透Face Recognition with Lo cal Binary Patterns这篇论文的时候我会加上这一点内容，现在先把人家博文上的解释加上。

一个LBP算子可以产生不同的二进制模式，对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生2^P种模式。很显然，随着邻域集内采样点数的增加，二进制模式的种类是急剧增加的。例如：5×5邻域内20个采样点，有220＝1,048,576种二进制模式。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。同时，过多的模式种类对于纹理的表达是不利的。例如，将LBP算子用于纹理分类或人脸识别时，常采用LBP模式的统计直方图来表达图像的信息，而较多的模式种类将使得数据量过大，且直方图过于稀疏。因此，需要对原始的LBP模式进行降维，使得数据量减少的情况下能最好的代表图像的信息。
为了解决二进制模式过多的问题，提高统计性，Ojala提出了采用一种“等价模式”（Uniform Pattern）来对LBP算子的模式种类进行降维。Ojala等认为，在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此，Ojala将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。如00000000（0次跳变），00000111（只含一次从0到1的跳变），10001111（先由1跳到0，再由0跳到1，共两次跳变）都是等价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111（共四次跳变）。

通过这样的改进，二进制模式的种类大大减少，而不会丢失任何信息。模式数量由原来的2^P种减少为 P ( P-1)+2种，其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说，二进制模式由原始的256种减少为58种，这使得特征向量的维数更少，并且可以减少高频噪声带来的影响。

    这里我不明白的点是：

    1. 这个等价模式类还好，但是根据这个说法整个不就是两种模式了吗，一种是等价模式，一种是混合模式，那又怎么会出现 P ( P-1)+2种模式呢？说白了还是这个式子是怎么推出来的不清楚。

    2. 这个模式的减少意思是这个LBP值从2^P种减少到P ( P-1)+2种吗？换句话说，00000000，00000111的模式一样，那影响他的LBP值吗？

    因为这些疑问，所以在我代码中也没有这部分内容，请见谅。

3. LBP特征匹配

如果将以上得到的LBP值直接用于人脸识别，其实和不提取LBP特征没什么区别，会造成计算量准确率等一系列问题。将一副人脸图像分为7x7的子区

域（如下图），并在子区域内根据LBP值统计其直方图，以直方图作为其判别特征。这样做的好处是在一定范围内避免图像没完全对准的情况，

同时也对LBP特征做了降维处理。

其实在上面提到的那篇论文里，分区的意义还在于我们可以根据不同的子区域给予不同的权重，比如说我们认为鼻子的权重大于边缘子区域对于整个图片的权重。权重的意思也就是这个部分对于匹配时整个图片的意义。

我们根据LBP值统计直方图，上面提到的LBP值有2^8=256种，其实也就是一个灰度图的直方图统计过程。只要我们把LBP值看做一个新的像素值。

在我的代码中判别其相似性的方法是，假设已知人脸直方图为M，训练人脸的直方图是N1，N2，，，Ni 我计算他们每个子区域内的直方图的差，再取平方获得最后的相似值，对比所有的相似值，取最小的。（这样很简单。。）

真正判断相似性的方法有：

大家可以去google一下，然后自己实现。

代码（这里说一句，虽然一般都是说LBP算法对于光照不敏感，但是大家看实验结果，带light的准确率都很低，，应该是我的代码问题，希望有大神如果愿意的话能告诉我哪里的问题）：

#coding:utf-8
#--------------------------------------------
#   作用：LBP人脸识别算法实现
#   日期：2015年4月11日
#   算法链接：http://blog.csdn.net/feirose/article/details/39552977
#           http://blog.csdn.net/zouxy09/article/details/7929531
#   实验结果：accuracy of centerlight is 0.333333
#             accuracy of glasses is 0.933333
#             accuracy of happy is 0.933333
#             accuracy of leftlight is 0.266667
#             accuracy of noglasses is 0.933333
#             accuracy of rightlight is 0.133333
#             accuracy of sad is 0.933333
#             accuracy of sleepy is 0.933333
#             accuracy of surprised is 0.866667
#             accuracy of wink is 0.800000
#   执行时间：494.759438799s
#--------------------------------------------
from numpy import *
from numpy import linalg as la
import cv2
import os
import math

# 为了让LBP具有旋转不变性，将二进制串进行旋转。
# 假设一开始得到的LBP特征为10010000，那么将这个二进制特征，
# 按照顺时针方向旋转，可以转化为00001001的形式，这样得到的LBP值是最小的。
# 无论图像怎么旋转，对点提取的二进制特征的最小值是不变的，
# 用最小值作为提取的LBP特征，这样LBP就是旋转不变的了。
def minBinary(pixel):
    length = len(pixel)
    zero = ''
    for i in range(length)[::-1]:
        if pixel[i] == '0':
            pixel = pixel[:i]
            zero += '0'
        else:
            return zero + pixel
    if len(pixel) == 0:
        return '0'

# 加载图像
def loadImageSet(add):
    FaceMat = mat(zeros((15,98*116)))
    j =0
    for i in os.listdir(add):
        if i.split('.')[1] == 'noglasses':
            try:
                img = cv2.imread(add+i,0)
                # cv2.imwrite(str(i)+'.jpg',img)
            except:
                print 'load %s failed'%i
            FaceMat[j,:] = mat(img).flatten()
            j += 1
    return FaceMat

# 算法主过程
def LBP(FaceMat,R = 2,P = 8):
    Region8_x=[-1,0,1,1,1,0,-1,-1]
    Region8_y=[-1,-1,-1,0,1,1,1,0]
    pi = math.pi
    LBPoperator = mat(zeros(shape(FaceMat)))
    for i in range(shape(FaceMat)[1]):
        # 对每一个图像进行处理
        face = FaceMat[:,i].reshape(116,98)
        W,H = shape(face)
        tempface = mat(zeros((W,H)))
        for x in xrange(R,W-R):
            for y in xrange(R,H-R):
                repixel = ''
                pixel=int(face[x,y])
                #　圆形LBP算子
                for p in [2,1,0,7,6,5,4,3]:
                    p = float(p)
                    xp = x + R* cos(2*pi*(p/P))
                    yp = y - R* sin(2*pi*(p/P))
                    if face[xp,yp]>pixel:
                        repixel += '1'
                    else:
                        repixel += '0'
                # minBinary保持LBP算子旋转不变
                tempface[x,y] = int(minBinary(repixel),base=2)
        LBPoperator[:,i] = tempface.flatten().T
        # cv2.imwrite(str(i)+'hh.jpg',array(tempface,uint8))
    return LBPoperator

    # judgeImg:未知判断图像
    # LBPoperator:实验图像的LBP算子
    # exHistograms:实验图像的直方图分布
def judgeFace(judgeImg,LBPoperator,exHistograms):
    judgeImg = judgeImg.T
    ImgLBPope = LBP(judgeImg)
    #  把图片分为7*4份 , calHistogram返回的直方图矩阵有28个小矩阵内的直方图
    judgeHistogram = calHistogram(ImgLBPope)
    minIndex = 0
    minVals = inf

    for  i in range(shape(LBPoperator)[1]):
        exHistogram = exHistograms[:,i]
        diff = (array(exHistogram-judgeHistogram)**2).sum()
        if diff<minVals:
            minIndex = i
            minVals = diff
    return minIndex

# 统计直方图
def calHistogram(ImgLBPope):
    Img = ImgLBPope.reshape(116,98)
    W,H = shape(Img)
    # 把图片分为7*4份
    Histogram = mat(zeros((256,7*4)))
    maskx,masky = W/4,H/7
    for i in range(4):
        for j in range(7):
            # 使用掩膜opencv来获得子矩阵直方图
            mask = zeros(shape(Img), uint8)
            mask[i*maskx: (i+1)*maskx,j*masky :(j+1)*masky] = 255
            hist = cv2.calcHist([array(Img,uint8)],[0],mask,[ 256],[0,256])
            Histogram[:,(i+1)*(j+1)-1] = mat(hist).flatten().T
    return Histogram.flatten().T

def runLBP():
    # 加载图像
    FaceMat = loadImageSet('D:\python/face recongnition\YALE\YALE\unpadded/').T
    
    LBPoperator = LBP(FaceMat) # 获得实验图像LBP算子
    
    # 获得实验图像的直方图分布，这里计算是为了可以多次使用
    exHistograms = mat(zeros((256*4*7,shape(LBPoperator)[1])))
    for i in range(shape(LBPoperator)[1]):
        exHistogram = calHistogram(LBPoperator[:,i])
        exHistograms[:,i] = exHistogram
    
    #　下面的代码都是根据我的这个数据库来的，就是为了验证算法准确性，如果大家改了实例，请更改下面的代码
    nameList = ['01','02','03','04','05','06','07','08','09','10','11','12','13','14','15']
    characteristic = ['centerlight','glasses','happy','normal','leftlight','noglasses','rightlight','sad','sleepy','surprised','wink']
    for c in characteristic:
        count = 0
        for i in range(len(nameList)):
            # 这里的loadname就是我们要识别的未知人脸图，我们通过15张未知人脸找出的对应训练人脸进行对比来求出正确率
            loadname = 'D:\python/face recongnition\YALE\YALE\unpadded\subject'+nameList[i]+'.'+c+'.pgm'
            judgeImg = cv2.imread(loadname,0)
            if judgeFace(mat(judgeImg).flatten(),LBPoperator,exHistograms)+1 == int(nameList[i]):
                count += 1
        print 'accuracy of %s is %f'%(c, float(count)/len(nameList))  # 求出正确率

if __name__ == '__main__':
    # 测试这个算法的运行时间
    from timeit import Timer
    t1=Timer("runLBP()","from __main__ import runLBP")
    print t1.timeit(1)