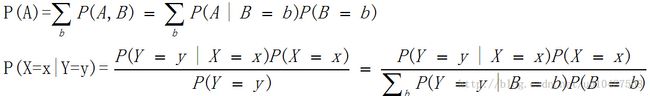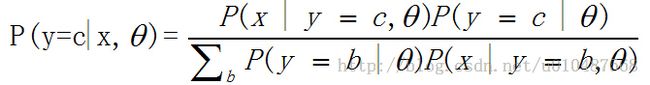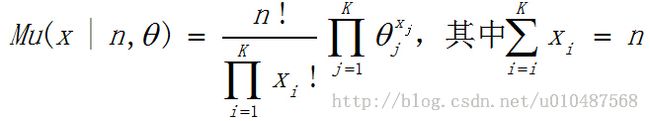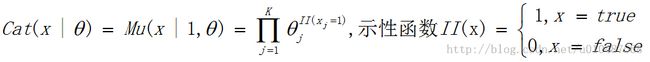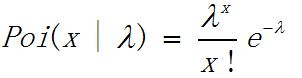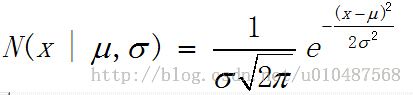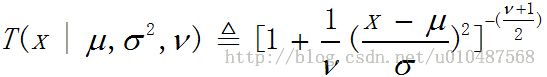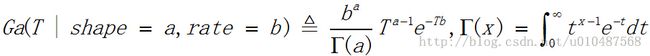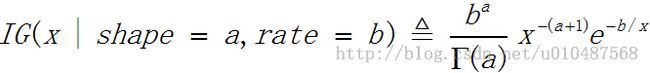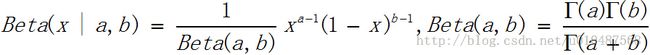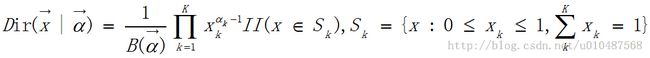MLAPP——机器学习的概率知识总结
《机器学习》课程使用的是Kevin P. Murphy所著的《Machine Learning A Probabilistic Perspective》这本英文原版教材,这本书从概率论这个数学角度独特阐述了机器学习的所有问题,需要较强的数学基础。因为是英文教材,特开一个专题在此记录自己的学习过程和各种问题,以供备忘和举一反三之用。
在讲解了机器学习的概述之后,第二章紧接着就开始讲述概率论的知识,通过后续的学习会发现,这些概率论知识有部分在本科的概率论课程中学习过,但是有很多其他部分是没有在现有的本科阶段甚至研究生阶段也很少涉及的知识点,在此做一个总结。
1、概率学派
频率学派:概率代表的是对一个试验重复执行N次,所关注的事件发生的频率。这里要求的是需要进行重复试验,这对于一般可重复执行的试验是比较好的标识方式,这也成为实验概率。
贝叶斯学派:概率代表的是人们对一个未知事件发生的不确定性的一种表征,这里不要求对这个事件进行重复试验。同时对于任何未知的事件,都可以用一个概率来表征人们对它的认识。
通过上述比较可以发现,对于某些不能重复试验的事件(比如生成灯管的工厂生成的灯管的平均使用寿命,进行重复实验是不现实的),使用贝叶斯概率的解释更加合理。因此在整个学习中都以贝叶斯学派为准。
2、基本知识
概率:事件空间Ω到实数域R的映射,对于每个事件A,都有一个实数p(A)与之对应,同时满足:(1)非负性,p(A)>=0;(2)规范性,p(Ω)=1;(3)可列可加性:p(A1+A2+…An) = p(A1)+p(A2)+…p(An)其中A1、A2…An都是互补相容的事件。
基本概率公式:
全概率公式和贝叶斯公式:
通用的贝叶斯分类器:
3、离散型分布
(1)二项分布Binomial
K为每次试验可能出现的结果,n为进行试验的次数。贝努利试验就是K={0,1}且n=1的试验,对于n(n>1)的n重贝努利实验就是二项分布,分布函数如下:
mean=θ,variance=nθ(1-θ)。二项分布描述的典型试验就是抛硬币,每次出现正面或者反面两种结果。这在机器学习的分类算法中用于描述二值的特征,也就是每个数据的特征的取值是两个状态(一般是0和1),用来表征当前数据是否有这个特征,因此可以使用二项分布来描述当前特征的分布。
(2)多项分布Multinormial
当每次试验出现的结果可能有K(K>2)种时,也就是一个特征的不仅仅是表征是否出现,而是需要用一个具体数值来表征该特征的影响大小,此时可以用多项分布进行描述。
此处,当K=2时也就是两种状态,可以看出多项分布就退化到了二项分布,可以看出x1=k,x2=n-k,x1+x2=n条件满足。其中,当n=1时,也就是只进行一次试验,此时的分布称为多维贝努利分布,因为每次的可能状态有K(K>2)个,也成为离散分布(discrete distribution)或者分类分布(categorical distribution),记为Cat(x|θ):
(3)泊松分布Poisson
变量X={0,1,2.....},λ>0,分布如下:
泊松分布可以用来模拟以时间序列发送的事件,具有无记忆性。
4、连续型分布
(1)正态分布Gaussian(Normal)
mean=u,mode=u,variance=σ^2。在统计学中应用非常广泛,首先两个参数非常好理解,分别是均值和标准差,同时,中心极限定理得到相互独立的随机变量的和的分布近似为高斯分布,可以用来模拟噪声数据;第三,高斯分布使用了最小的假设也就是拥有最大熵;第四,数学形式相对简单,非常利于实现。
(2)Student t分布
mean=u,mode=u,variance=νσ^2/(ν-2),ν>0为自由度,方差在ν>2时有定义,均值在ν>1时有定义。此分布形式上与高斯分布类似,弥补了高斯分布的一个不足,就是高斯分布对离群的数据非常敏感,但是Student t分布更鲁棒。一般设置ν=4,在大多数实际问题中都有很好的性能,当ν大于等于5时将会是去鲁棒性,同时会迅速收敛到高斯分布。
特别的,当ν=1时,被称为柯西分布(Cauchy)。
(3)拉普拉斯分布Laplace
mean=u,mode=u,variance=2b^2。也被称为双侧指数分布,引出了绝对值的指数次方,因此在x=u处不可导。b(b>0)为缩放因子,用来调节数据的分散程度。拉普拉斯分布对离群数据的鲁棒性更好。同时,在x=u处给予了比高斯分布更大的概率密度,这个性质可以用来修正模型中稀疏的数据。
(4)Gamma分布
mean=a / b,mode=(a-1) / b,variance=a / b^2,mean在a>1时有定义,variance在a>2时有定义。其中变量T的范围为T>0,a>0称为形状参数,b>0称为速率参数。
- Exponential分布:a=1,b=λ时,Expon(x|λ)=Ga(x|1,λ),这个分布描述了连续的泊松过程,与离散型的泊松分布共轭。
- ErLang分布:ErLang(x|λ)=Ga(x|2,λ)
- Chi-Squared分布(卡方分布):ChiSq(x|v)=Ga(x|v/2,1/2),这是N个高斯分布的随机变量的平方和所服从的分布。
mean=b / (a-1),mode=b / (a+1),variance=b^2 / (a-1)^2(a-2),其中mean在a>1时定义,variance在a>2时定义。
(5)Beta分布
定义在[0,1]区间上,要求a>0,b>0,当a=b=1时就是[0,1]上的均匀分布。mean=a / (a+b), mode=(a-1) / (a+b-2), variance = ab / (a+b)^2(a+b+1)。这个分布与离散的二项分布是共轭的,在朴素贝叶斯分类应用中,当似然分布为二项分布时,选择Beta分布为共轭先验分布,则后验分布也为Beta分布,非常便于实际操作和计算。
(6)Pareto分布
mean=km/(k-1)(k>1),mode=m,variance=mk^2 / (k-1)^2(k-2)(k>2),这个分布对应有一个Zipf's 定律,用来描述单词的排名和其出现的频率的关系。x必须比一个常数m要大,但是不能超过k,当k为无穷大时,这个分布会趋于δ(x-m)。上述分布在信息检索中对索引构建中的词频估计很有效。
(7)狄利克雷分布Dirichlet
mean(Xk)=ak/a0, mode(Xk) = (ak - 1) / (a0 - K), variance(Xk) = ak(a0-ak) / a0^2(a0+1)。这是beta分布在多维条件下的分布,对应的参数和变量都是一个向量,这个分布与离散的多项分布时共轭的,在朴素贝叶斯分类应用中,似然使用多项分布时,选择Dirichlet分布为先验分布,得到后验分布也为Dirichlet分布。
以上对机器学习中使用到的概率分布做了一个总结,供后续学习时备忘和复习。