从2-3-4树谈到Red-Black Tree(红黑树)
从2-3-4树谈到Red-Black Tree(红黑树)
译者:July。
出处:http://blog.csdn.net/v_JULY_v 。
在上一篇文章--从B树、B+树、B*树谈到R 树里已提到2-3-4树,那么本文,咱们就从2-3-4树开始谈起,然后谈至红黑树。因为理解了2-3-4树,红黑树也就没有任何问题了。同时,虽然红黑树在本blog已有过非常详尽的阐述。但个人此后对红黑树又有了不少新的认识,雨打风吹去,已体味到另一番意境。
Ok,本文大部分内容翻译自此文档:Left-Leaning Red-Black Trees, Dagstuhl Workshop on Data Structures, Wadern, Germany, February, 2008.这个文档本人在之前介绍红黑树的文章里早已推荐过。但我相信,如果不真正完全摆在读者面前,他们是不能最大限度的体会到一个东西的价值与精彩的。
So,旅程开始,祝旅途愉快。
第一节、2-3-4树
2-3-4 树在计算机科学中是阶为 4 的B树。根据维基百科上的介绍:大体上同B树一样,2-3-4 树是可以用做字典的一种自平衡数据结构。它可以在O(log n)时间内查找、插入和删除,这里的 n 是树中元素的数目。2-3-4 树在多数编程语言中实现起来相对困难,因为在树上的操作涉及大量的特殊情况。红黑树实现起来更简单一些,所以可以用它来替代(红黑树稍后介绍)。以下就是一棵2-3-4树:
2-3-4 树把数据存储在叫做元素的单独单元中。那么请问,到底什么是2-3-4树呢?顾名思义,就是有2个子女,3个子女,或4个子女的结点,这些含有2、3、或4个子女的结点就构成了我们的2-3-4树。所以,它们组合成结点,每个结点都是下列之一:
2-节点,就是说,它包含 1 个元素和 2 个儿子,
3-节点,就是说,它包含 2 个元素和 3 个儿子,
4-节点,就是说,它包含 3 个元素和 4 个儿子 。
4-结点
每个儿子都是(可能为空)一个子 2-3-4 树。根节点是其中没有父亲的那个节点;它在遍历树的时候充当起点,因为从它可以到达所有的其他节点。叶子节点是有至少一个空儿子的节点。同B树一样,2-3-4 树是有序的:每个元素必须大于或等于它左边的和它的左子树中的任何其他元素。每个儿子因此成为了由它的左和右元素界定的一个区间。如下图所示(你可以看到,图中这棵2-3-4树是由2-结点,3-结点,4-结点元素组成的):
2-3-4 树是紅黑树结构的一种等同,这意味着它们是等价的数据结构。换句话说,对于每个 2-3-4 树,都存在着至少一个数据元素是相同次序的红黑树。在 2-3-4 树上的插入和删除操作也等价于在红黑树中的颜色翻转和旋转。这使得它成为理解红黑树背后的逻辑的重要工具(还是如此,红黑树稍后介绍,路得一步一步来)。
1.1、2-3-4树的查找
2-3-4树中查找结点,怎么查找呢?分为以下几个步骤:
1、把要查找的结点与根结点相比较
2、根据左小右大的原则,寻找含有要查找结点的区间
3、若找到了,则直接返回该结点,否则,在其子女中继续递归寻找。
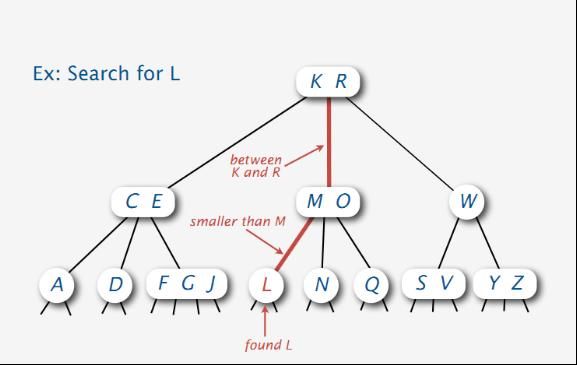
如下图所示,在下面这棵2-3-4树中寻找L结点:
1.2、2-3-4树的插入
插入某个结点之前,一般我们先在2-3-4树中寻找是否存在该插入结点(若存在,当然也就没有必要再插入了),如果树中不存在该结点,则执行插入操作。
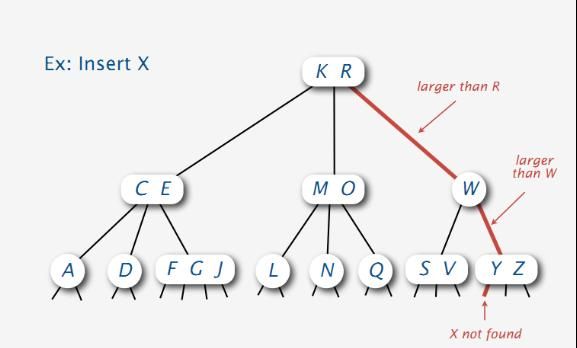
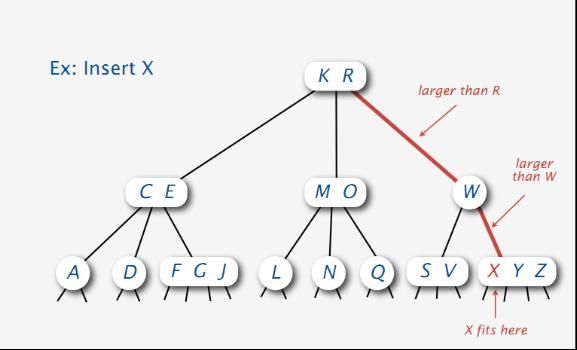
1.2.1、插入形式一:3-结点元素中插入结点
没有找到,则在含有Y Z的结点元素插入X:
1.2.2、插入形式二:
以下插入H结点,在F G J区间上发现H没有找到后,
且F G J区间上已经没有空间来插入H结点了,这个时候怎么办呢?:
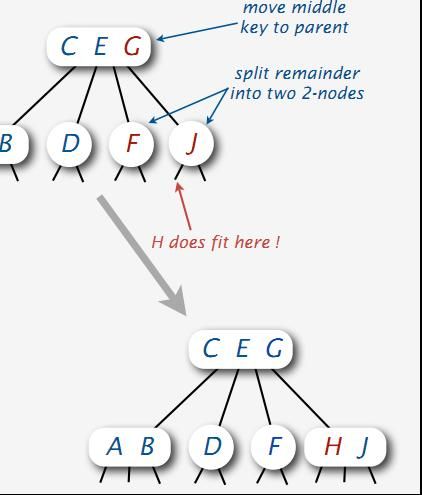
当没有空间执行插入操作的时候,咱们当然得寻找空间来执行插入。怎么寻找呢?看下图: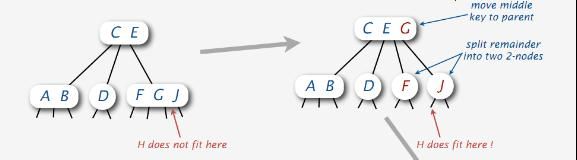
由上图,我们发现,H在区间F G J 上没有空间执行插入的时候,我们首先参试着让G元素上移至C E区间,组成C E G根结点,然后分裂F G区间,F和G各自成为独立的元素。当我们发现,H依然不能作为J的子女进行插入时,我们想到了一种折中的办法,这种办法就是,如下图所示,H插入到J元素旁,成为H J区间,F元素不作变动:
所以,当发现没有空间可执行插入结点的情况时,我们作如下对策:
1、分裂父母结点
2、然后再插入结点
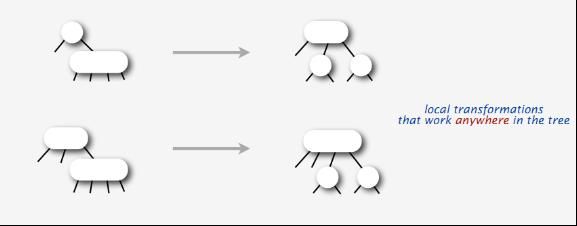
上述的第1点具体怎么分裂呢?分裂的两种情况如下图所示:
下面再具体分析下上述两种分裂情况:
分裂情况1、如下图所示D-K Q W,区间K Q W分裂,Q上移与原根结点D组成新的根结点区间D Q,K和W各自分裂成独自区间,D-K Q W最终分裂成D Q-K-W:
分裂情况2、如下图所示D H-K Q W分裂,K Q W区间中的Q元素上移与D H组成根元素区间D H Q,K和W 分裂,最终D H-K Q W分裂成D H Q-K-W:
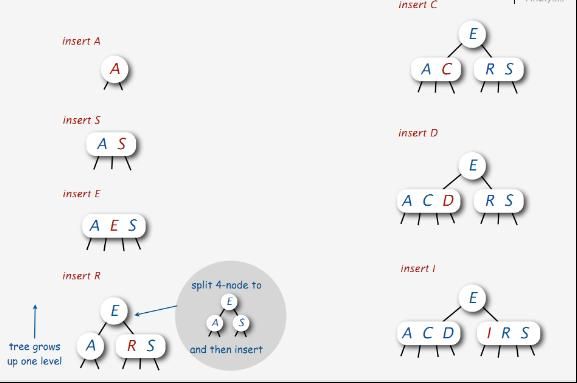
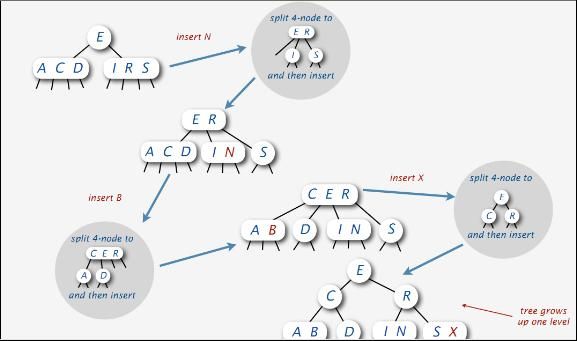
下图是逐步在2-3-4树中依次插入元素A、S、E、R、C、D、I。从中你可以看到
1、当插入元素R时,A E S区间分裂,E成为新的根元素,而要插入的R与S移至一起成为E的右儿子。
2、当插入C、D、I时,都是直接找到相对应的区间,各自插入。不必啰嗦,下图已经很形象了。
但下面,继续在上述的A、S、E、R、C、D、I插入操作的基础上之后,再依次插入N、B、X各元素时,情况,就比较复杂了,但下图还是很清晰的表明了各种插入操作及相关元素的调整情况,在此不赘述:
下图所示的是在2-3-4树中插入结点的insert代码:
到此,插入情况已经阐述完,删除情况略过。接下来,咱们来分析下2-3-4树的平衡情况。
1.3、2-3-4树的平衡
2-3-4树的高度为:
1、最坏情况,logn,树中全部都是2结点元素(即如第一节所述的全都是包含一个元素和2个儿子的结点。如此图所示,树中全部都是这样的结点:
2、最好情况,log4N=1/2logN,树中全部都是4结点元素(即如第一节所述的全都是包含 3 个元素和 4 个儿子 的结点,如此图所示,树中全部都是这样的结点:
3、3结点情况是中间情况,即包含 2 个元素和 3 个儿子,
第二节、Red-Black trees(红黑树)
2.1、红黑树与2-3-4树的等价性
上述第一节中,总是说红黑树是与2-3-4树等价的数据结构,下面,我来挖掘出他们的之间的等价性给你看,看看在红黑树上是否能看到2-3-4树的影子?ok,请看下图:
恩,yeah,不知你是否也看明白了:红黑树真的就是一种2-3-4树,为什么这么说呢?因为从上图中,你能轻易的看到,2-3-4树中的3-结点,和4-结点分裂后,的确就是红黑树中的结点元素形式了。
Ok,可能你还不相信,再送给你一幅图,从中,你是否已看出了丝毫端倪?: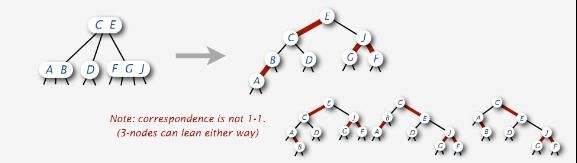
在上面的图中,你可以清楚的看到图中左部分的2-3-4树最终能转换成一棵红黑树。不过,在上述情况下,红黑树最终将调整如下:
2.2、红黑树的插入操作
下图所示的代码是红黑树的插入操作代码:
在红黑树中,有一个非常重要的基础操作,那就是左旋与右旋,在本blog之前的红黑树系列已经对这两种情况进行过详尽的阐述,下图是左旋和右旋各自的操作及对应的代码:
而红黑树的左旋、右旋操作情况中与2-3-4树对应起来的情况如下图所示: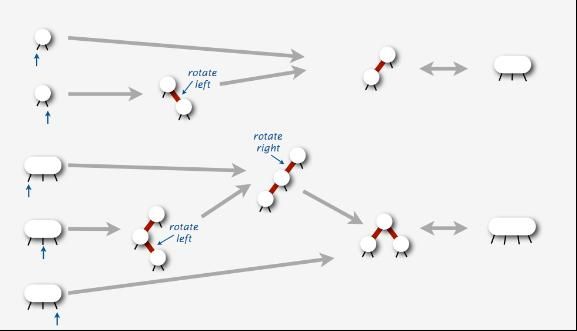
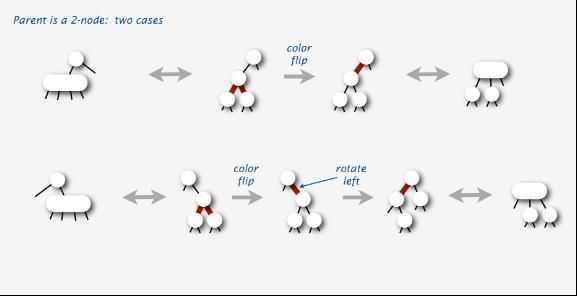
2.2.1、红黑树的插入情况一:父母是2-结点
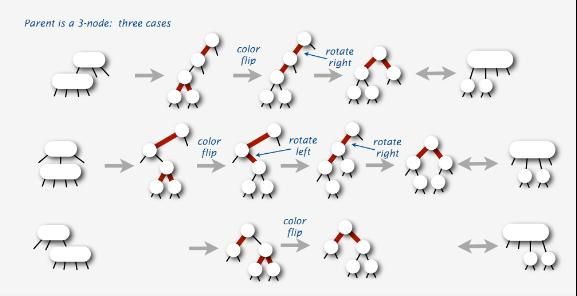
2.2.2、红黑树的插入情况二:父母是3-结点
其余一切类似插入操作不再阐述。关于红黑树的删除操作在本blog内已经有所具体的阐述,本文不再叙述。全文完。
备注:本blog内的6篇红黑树文章如下:
初步了解红黑树,请看此文:教你透彻了解红黑树
关于红黑树的算法实现,请看此文(对红黑树的删除情况有比较清晰的阐述):红黑树算法的实现与剖析
红黑树的c源码实现,请看此文:红黑树的c源码实现与剖析
C++源码实现,请看此文:红黑树的c++完整实现源码
本红黑树系列中一篇重要的文章:红黑树插入和删除结点的全程演示
其余文章还有:一步一图一代码,R-B Tree
参考文献:
1、:Left-Leaning Red-Black Trees, Dagstuhl Workshop on Data Structures, Wadern, Germany, February, 2008.。可以在这里下载到:http://www.cs.princeton.edu/~rs/talks/LLRB/RedBlack.pdf。
2、本blog内6篇红黑树文章:红黑树(Red-Black Tree )。
版权所有,侵权必究。本blog内任何内容严禁用于任何商业用途,违者永久追究法律责任。