Chapter 2 | Linked Lists--查找循环链表中的环的开始结点
2.5 Given a circular linked list, implement an algorithm which returns node at the beginning of the loop.
DEFINITIONCircular linked list : A(corrupt) linked list in which a node’s nextpointer points to an earlier node, so as to make a loop in the linkedlist.
EXAMPLE
Input : A->B->C->D->E->C [the same C as earlier]
Output : C
译文:给定一个循环链表,实现一个算法返回这个环的开始结点。
定义:循环链表就是链表中一个结点的指针指向先前出现的结点,导致链表中出现环。
例子:
输入:A->B->C->D->E->C [这个C就是先前出现的结点]
输出:C
这个题目分为两步,首先判断链表中是否存在环,然后再去寻找这个环的开始结点。
判断链表中是否存在环,最常采用的方法是用快慢指针(一般设置快指针两倍于慢指针,这样快指针遍历的结点数减去慢指针的正好是慢指针遍历的结点数)。快慢指针只有在存在环的链表中才会相遇,所以我们可以通过是否两个指针会相遇来判断链表中是否存在环。
这里稍稍麻烦的就是寻找环的开始结点,这里我们通过简单的数学公式来推导一下。
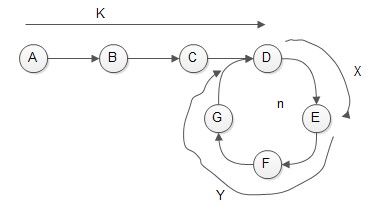
根据上图,我们假定在判断是否存在环时,快慢指针在E点相遇。那么快慢指针走过的结点数分别为:
慢指针:K + X + nP = m (1);
快指针:2 * m (2);
K为链表头结点到环开始结点的结点数,X为环开始结点到相遇结点的结点数,n为环的结点数,P为慢指针遍历环的圈数。
联立(1)(2)有 2*m - m = K + X + nP = nQ; Q为快慢指针相遇时,快指针比慢指针多遍历环的圈数,快慢指针相遇时,二者遍历结点的差值恰是环长的整数倍。
所以有 K + X = n(Q - P); 很明显,n(Q - P)为环结点的整数倍,即快慢指针相遇点离链表头结点Head(这里是A结点)的距离恰是环长的整数倍。
结合上式,再从图可知存在关系:K + X = N(X + Y); N为正整数,N的值受K的影响。
所以我们可以将其中一个指针移至链表头结点Head,同时两结点以相同速度再次相遇就是环的开始结点。算法出来了,直接贴代码
Node* findBeginning(Node *pHead)
{
if (NULL == pHead)
return NULL;
Node *fast = pHead;
Node *slow = pHead;
/*判断是否存在环*/
while (fast->pnext != NULL) //两种情况会跳出循环
{
fast = fast->pnext->pnext;
slow = slow->pnext;
if (NULL == fast)
return NULL;
if (fast == slow)
break;
}
if (NULL == fast->pnext) //判断是哪种情况导致跳出循环
return NULL;
/*查找环起点*/
fast = pHead;
while (fast != slow)
{
fast = fast->pnext;
slow = slow->pnext;
}
return fast;
}另外曾看到网上有直接采用哈希表来寻找环的起始节点。思路就是寻找第一个重复结点,就是遍历链表,以地址为哈希表的键值,每出现一个地址,就将该键值对应的实值置为true,当某个键值对应的实值已经为true时,说明这个地址之前已经出现过,就是环的开始结点。想法很好,但必须保证这个链表当中存在环,才奏效。如果链表结构是这样子就不行了: A -> B -> C -> D -> E - > C -> NULL;所以在测试的时候,不要构建这样的链表来测试哦。既然这样的话,还是上面那个算法比较好。