主成分分析与白化预处理
上一节介绍了主成分分析应用于2维数据。现在使用高维的图像数据来试试效果。
原始图像如图1所示。
图1
每个图片都是12*12的小patch,原始数据是一个144*10000的矩阵x。
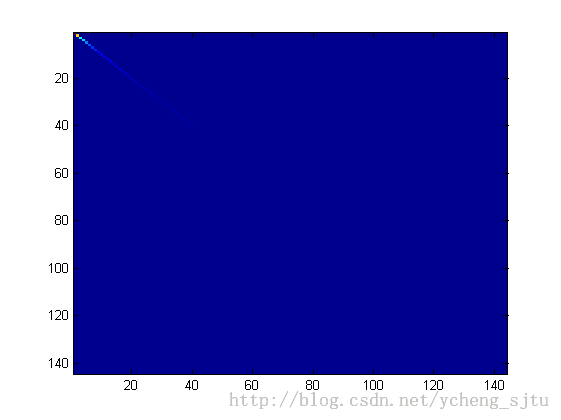
在使用了PCA旋转之后,可以检查一下此时的协方差矩阵是否已经成功变成对角阵了,如图2所示。
avg=mean(x,1);
x=x-repmat(avg,size(x,1),1);
xRot = zeros(size(x)); % You need to compute this
[u,s,v]=svd(x*x'/size(x,2));
xRot=u'*x;
covar = zeros(size(x, 1)); % You need to compute this
covar=xRot*xRot'/size(xRot,2);
figure('name','Visualisation of covariance matrix');
imagesc(covar);</span>
图2
接下来我们需要找到使得图片方差保持在90%以上的k值。即取协方差矩阵最大的k个特征值用来后面降维。
k = 0; % Set k accordingly partial=0; total=sum(diag(s)); for k=1:size(x,1) partial=partial+s(k,k)/total; if partial>0.9 break; end end</span>这个k值是43。如果要求保持99%的样本方差,则k取116。
确定了k值之后,就可以用PCA降维了。
xHat = zeros(size(x)); xHat=u(:,1:k)*u(:,1:k)'*x;</span>可视化一下,可以看到用43个特征来重构出144维图片的效果,还是不错的。如图3。
图3
而如果像前文所说,取能保持99%的k值116的话,效果会更好,如图4。
图4
接下来还可以进行PCA白化。
epsilon = 0.1; xPCAWhite = zeros(size(x)); xPCAWhite=diag(1./sqrt(diag(s)+epsilon))*u'*x;</span>然后我们验证一下白化之后的新的协方差矩阵是否是对角阵,如图5。
covar = zeros(size(xPCAWhite, 1)); % You need to compute this
covar=xPCAWhite*xPCAWhite'/size(xPCAWhite,2);
figure('name','Visualisation of covariance matrix');
imagesc(covar);</span>
图5
最后是ZCA白化的处理效果,可以看出ZCA在不降维的情况下,通过变换将原始数据的边缘提取了出来,如图6。
xZCAWhite = zeros(size(x));
xZCAWhite=u*xPCAWhite;
figure('name','ZCA whitened images');
display_network(xZCAWhite(:,randsel));
figure('name','Raw images');
display_network(x(:,randsel));
图6
欢迎参与讨论并关注本博客和微博以及知乎个人主页后续内容继续更新哦~
转载请您尊重作者的劳动,完整保留上述文字以及文章链接,谢谢您的支持!