《数据结构与算法分析》第十二章，AA-树，Treap树简要介绍与实现

前言：

       这里我要介绍的这4个数据结构，是在《数据结构与算法分析》一书上的最后4种数据结构了。这些数据结构给出来了实现的代码，实现的难度并不大，一天之内我就把这四个数据结构的测试代码给调通了。

       这四个数据结构里，一个是红黑树的变种，对红黑树进行了化简，一个是为了多维查询范围所设计的数据结构。最后一个是变种的斐波那契堆,目的同样是为了化简实现。本来我想这几个数据结构就没必要再写了吧，后来想想。整个《数据结构与算法分析》这本书我都实现并写了博客，最后还是要做到有始有终吧。因为这几种数据结构的实现，对于我已经不再困难，主要是理解思想。因此在这里的介绍，主要还是介绍思想与展示一下调试的结果。

我的github：

我实现的代码全部贴在我的github中，欢迎大家去参观。

https://github.com/YinWenAtBIT

介绍：

AA树：

一、发明：

AA树是Arne Andersson教授在他的论文"Balancedsearch trees made simple"中介绍的一个红黑树变种，设计的目的是减少RB树考虑的cases。

二、特性：

1、AA-Tree是RB-Tree的一种变型，是红黑树

2、“红”结点只能作为结点的右孩子，“黑”结点均可；

3、结点中的level相当于RBT中的结点的黑高度；

4、“红”结点的level与其父结点的level相同；

5、“黑”结点的level比其父结点的level小1；

6、左孩子的level比父结点小1，右孩子的level比父结点小0或1；

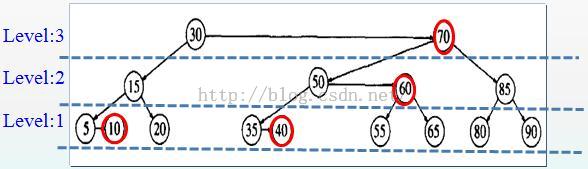
上图与《数据结构与算法分析》一书中给出的图相同，其中，10,40,60,70为红色的右孩子。

三、插入操作：

插入操作与删除操作，都有可能破坏AA树的4,5性质，因此，在每次完成了插入操作或者删除操作之后，需要进行树的性质修复。之所有说AA树是化简 的红黑树，就是因为此时的修复工作简单了很多。

在上图中插入45或者2，将会破坏AA树的性质，需要使用插入修复。

插入修复：

情况1：

如上插入节点2，在左孩子插入之后，导致左孩子的level上升，破坏性质5（左孩子只能是黑色），解决的方式是通过一次右旋转。在这里我们命名为Skew操作，对右旋转做了一个封装，判断是否左孩子的level与父亲的level是否相等

AATree skew(AATree T)
{
	if(T->level == T->left->level)
		T = rightSingleRotate(T);
	return T;
}

情况2：

如上插入节点45，在右孩子插入之后，导致两个红色的孩子连在一起了（这里实际上是两个水平链接，实际实现时不再使用颜色标记，只记录level），破坏性质5（左孩子只能是黑色），解决的方式是通过一次左旋转。在这里我们命名为Split操作，对左旋转做了一个封装，判断是否右孩子的右孩子的level与父亲的level是否相等。

插入编码：

AATree insert(ElementType item, AATree T)
{
	if(T == NullNode)
	{
		T = (AATree)malloc(sizeof(struct AANode));
		if(T == NULL)
			exit(1);

		T->Element = item;
		T->level  = 1;
		T->left = T->right = NullNode;

		return T;
	}
	else if(item < T->Element)
		T->left = insert(item, T->left);
	else if(item> T->Element)
		T->right = insert(item, T->right);

	T = skew(T);
	T = split(T);
	return T;
}

四、删除操作

删除操作的实现与普通的查找二叉树相同，不过由于AA树的特性，一个节点如果不是叶子节点，那么它必定有一个右孩子。我们就可以总是用右孩子中的最大节点来代替该节点，然后删除掉右孩子中的最大节点。实现的时候，我们使用两个静态变量来跟踪该删除的节点和右孩子最大的节点。完成删除之后，我们有可能破坏了树的level。

如果删除的是一个左孩子，或者右孩子，都有可能导致父亲节点比左右孩子的level高出2。那么此时就要降低父亲节点的level。并且如果导致了右孩子的level比父亲level高，右孩子的level要等于父亲的level。

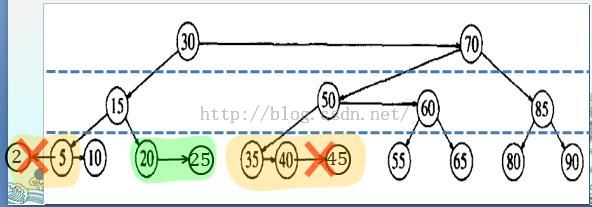
经过这样的处理之后，同一个level上，最多会出现6个节点，如下图所示（删除1后，父亲节点2高出做孩子两个level，下降为1，节点5高于父亲节点，下降为1，所有节点于是都处于level 1）

解决的方案就是连续的Skew操作加上Split操作，在这里就不进行分析了。

删除编码：

AATree remove(ElementType item, AATree T)
{
	static Position DeletePtr, LastPtr;
	if(T != NullNode)
	{
		LastPtr = T;
		if(item < T->Element)
			T->left = remove(item, T->left);
		else
		{
			DeletePtr = T;
			T->right = remove(item, T->right);
		}

		if(T == LastPtr)
		{
			if(DeletePtr != NullNode && item == DeletePtr ->Element)
			{
				DeletePtr->Element = T->Element;
				DeletePtr = NullNode;
				T = T->right;
				free(LastPtr);
			}
		}

		else
		{
			if(T->left->level < T->level -1 || T->right ->level < T->level -1)
			{
				if(T->right->level > -- T->level)
					T->right->level = T->level;

				T= skew(T);
				T->right = skew(T->right);
				T->right->right = skew(T->right->right);
				T = split(T);
				T->right = split(T->right);
			}
		}
	}

	return T;
}

测试结果图：

        

左图是按照该书中顺序插入节点之后的图，右图是删除根节点70之后的图。

Treap树：

一、特性：

Treap树基本上是最简单的二叉查找树了。它在树中添加了一个新的元素，优先级，就好比优先队列，优先级越小，越靠近树根。因此，该树只需要满足如下性质：

1.如果v是u的左孩子，则key[v] < key[u].

2.如果v是u的右孩子，则key[v] > key[u].

3.如果v是u的孩子，则priority[u] > priority[u].

这两个性质的结合就是为什么这种树被称为“treap”的原因，因为它同时具有二叉查找树和堆的特征

二、插入与删除

实现插入与删除特别简单，实用递归方法，每次插入之后进行判断，如果违反了堆的性质，进行旋转即可。

删除的方式是通过把要删除的点旋转到叶子节点，最后旋转为了NullNode的左节点，然后删除。中途的旋转会保证一直满足堆的性质。

三、编码实现：

插入：

TreapTree insert(ElementType item, TreapTree T)
{
	if(T == NullNode)
	{
		T = (TreapTree)malloc(sizeof(struct TreapNode));
		if(T == NULL)
			exit(1);

		T->Element = item;
		T->Priority  = rand()%Infinity;
		T->left = T->right = NullNode;

		return T;
	}
	else if(item < T->Element)
	{
		T->left = insert(item, T->left);
		if(T->Priority > T->left->Priority)
			T = rightSingleRotate(T);
	}
	else if(item> T->Element)
	{
		T->right = insert(item, T->right);
		if(T->Priority > T->right->Priority)
			T = leftSingleRotate(T);
	}

	return T;
}

删除：

TreapTree remove(ElementType item, TreapTree T)
{
	static Position DeletePtr, LastPtr;
	if(T != NullNode)
	{
		if(item < T->Element)
			T->left = remove(item, T->left);
		else if(item > T->Element)
		{
			T->right = remove(item, T->right);
		}
		else
		{
			if(T->left->Priority < T->right->Priority)
				T = rightSingleRotate(T);
			else 
				T = leftSingleRotate(T);

			if(T != NullNode)
				T = remove(item, T);

			else
			{
				free(T->left);
				T->left = NullNode;
			}
		}
	}

	return T;

}

测试：

左图是插入后形成的Treap树，表示为节点值与优先值。右图是删除节点70之后的树。

总结：

到这里，整个《数据结构与算法分析》上的数据结构与算法，就算是全部都学习完了，学习的收获非常大，我会写一篇新的感想博客来好好说说