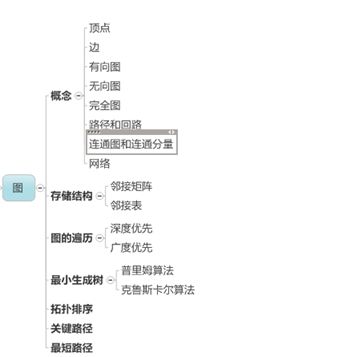
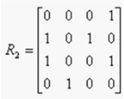数据结构之图
文章脉络图：
图由点集合和边集合组成，记做G=(V,E)，其中点集合不能为空且应该有穷，边集合可以为空。在有关图的概念方面，大部分看名知意，只解释其中几个概念：
- 有向图：边有方向，用<Vi,Vj>表示；无向图：边没有方向，用(Vi,Vj)表示。
- 完全图：每两个顶点之间都有连线，有向完全图的边有n（n+1）个；无向完全图有n（n+1）/2个边。
- 路径和回路：路径是指从一个点到另外一个点走过的路径和长度；回路是指从一个点出发再回到一个点的路径;简单回路是指中间没有重复经过的点。
- 连通图和连通分量：连通图是指任意两个点之间可以到达；在有向图中要求更严格，任意两点可以相互到达。连通分量是指把连通图分解成子连通图，子连通图的称呼。
- 网络：边带有权值的图。
邻接矩阵：反映的是顶点间的相邻关系。一个n行n列的矩阵表示由n个顶点的图，如果(i,j)或者<i,j>属于边集合，则矩阵中第i行j列的值为1，否则为0。
例如
的邻接矩阵为
。
从邻接矩阵的定义可以推断，无向图的邻接矩阵是对称的；有向图的邻接矩阵是非对称的。对于无向图而言，邻接矩阵第i行的和为邻接顶点i的度；对于有向图，邻接矩阵第i行表示的和是顶点i的出度，第i列的和表示顶点i的入度。
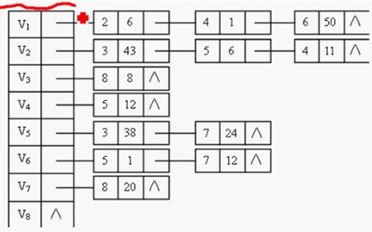
邻接表：为图的每个顶点建立一个链表，第i个链表中的结点表示与顶点i相关的边。
例如
的邻接表为
。
图的遍历
深度优先：
1．首先访问出发顶点V
2. 依次从V出发搜索V的每个邻接点W;
3. 若W未访问过，则从该点出发继续深度优先遍历；它类似于树的前序遍历。
广度优先：
1．首先访问出发顶点V
2．然后访问与顶点V邻接的全部未访问顶点w、X、Y…
3．然后再依次访问W、X、Y…邻接的未访问的顶点；
例如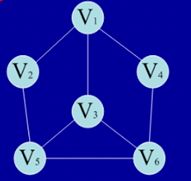
的深度优先遍历为：V1 V2 V3 V4 V5 V6；广度优先遍历为：V1 V2 V5 V3 V6 V4。
最小生成树
包含图所有顶点的树，成为图的生成树，各边权值之和最小的树成为最小生成树。
普里姆算法：
1. 定义出发点为一个集合
2. 其它点为另外一个集合
3. 找到顶点和其它点的距离，不可到达为无穷大
4. 每确定一个点，则把这个点当做出发点集合中的点，从此点开始再次循环规则
克鲁斯卡尔算法：
1. 先确定各个点之间的距离
2. 画出各个点
3. 距离从小到大排序，依次加入画的顶点中（但是避免形成回路，如果形成回路，则忽略此距离），直到各个点之 间可以连通
拓扑排序
用有向边表示各顶点活动开始的先后顺序，这些顶点组成的网络成为AOV网络。对一个有向无环图的顶点排成一个线性序列，使得有向边起点排在该有向边终点前的序列称之为拓扑序列。拓扑排序不一定唯一。
1. 找到入度为0的点，作为起点
2. 起点完成后，删除该起点的出度
3. 在剩余的aov网络中重复此过程
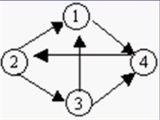
例如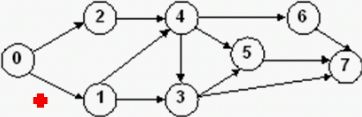
的拓扑排序为：02143567或01243657或02143657或01243567。
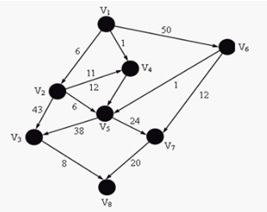
关键路径
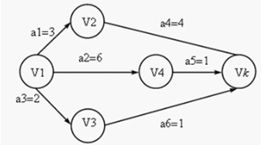
AOV网络中，如果边上的权表示完成该活动所需的时间，则称这样的AOV为AOE网络。其中关键路径是最长的一条路径。如下：
的关键路径为V1--V2--Vk或V1--V4--Vk。
数据结构暂时先总结到这里，还有很多等待修补的知识，接下来是编译原理的一些总结，欢迎指针……