协同过滤 --- 数据挖掘学习笔记

Collaborative Filtering

1.协同过滤CF

    最近你想看电影了，但是不知道看什么好，想要了解电影的推荐信息，通过什么途径呢？

    比如向问朋友，问老师，问亲友，但是毕竟每个人的品味不同，而且现在可选择的商品或电影太多太多了，不肯得到很好的推荐效果，知道你确实想要什么。

    协同过滤推荐（Collaborative Filtering recommendation）是在信息过滤和信息系统中正迅速成为一项很受欢迎的技术。与传统的基于内容过滤直接分析内容进行推荐不同，协同过滤分析用户兴趣，在用户群中找到指定用户的相似（兴趣）用户，综合这些相似用户对某一信息的评价，形成系统对该指定用户对此信息的喜好程度预测。

    一个协作型过滤算法通常的做法是对一大群人进行搜索， 并从中找出与我们品味相近的一小群入。算法会对这些人所偏爱的其他内容进行考查，并将它们组合起来构造出一个经过排名的推荐列表。有许多不同的方法可以帮助我们确定哪些人与自己的品味相近，并将他们的选择组合成列表。

2. 协同过滤种类

    user-based cf 是基于用户的协同过滤，通过不同用户对item的评分来评测用户之间的相似性，基于用户之间的相似性做出推荐；

    item-based cf 是基于物品的协同过滤，通过用户对不同item的评分来评测item之间的相似性，基于item之间的相似性做出推荐；

3.user-based CF 基于用户的协同过滤

    实现思想：

    1. 获取偏好：获取不同用户对item的评分列表。key是用户，value是用户对每个item的评分(item1:3, item2 : 5 ...etc)

    2. 相似度评价：找出相似的用户。（欧式距离评价，皮尔逊相关系数评价...etc）

    3. 依据相似度评价，寻找topMatch,找出某个人最相似的前N个人。

    4. 推荐物品，即找出相似的人，如何推荐，推荐哪些item。

    

    每个步骤都是要再三思考的：

    比如相似度评价，就要很多方法，欧式距离在空间上的绝对距离来评价，需要量纲一致才能出现比较好的效果。而皮尔逊相关系数是在方向上，余弦相似度，以向量的夹角来判断相似性，不要求量纲的绝对一致就能出现比较好的效果。还有找出相似的用户，如何推荐商品，是直接推荐它没看过的商品，还是根据大家对某个item的评分来决定是否要推荐。

3.1 为用户推荐电影

    下面用一个例子来说明：

    1. 获取偏好：

     这个属于数据源的收集，每个用户对某样商品的评分，经过etl形成类似如下的格式，里面包含了每个用户，对它所评价过的电影的评分列表。

# A dictionary of movie critics and their ratings of a small
# set of movies
critics={'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,
 'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5, 
 'The Night Listener': 3.0},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5, 
 'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0, 
 'You, Me and Dupree': 3.5}, 
'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0,
 'Superman Returns': 3.5, 'The Night Listener': 4.0},
'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0,
 'The Night Listener': 4.5, 'Superman Returns': 4.0, 
 'You, Me and Dupree': 2.5},
'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0, 
 'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0,
 'You, Me and Dupree': 2.0}, 
'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,
 'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},
'Toby': {'Snakes on a Plane':4.5,'You, Me and Dupree':1.0,'Superman Returns':4.0},
'shengli': {'Snakes on a Plane':4,'You, Me and Dupree':2.0,'Superman Returns':5.0,'Just My Luck':3.0},
}

    2.相似度评价

    相似度评价的算法，这里列举2个，欧式距离和皮尔逊相关系数。公式就不再这里列出了，可以参见：距离和相似度度量

    距离的计算方法签名都是一样的，第一个参数是偏好集合，第二个是this用户，第三个是和this用户比较的用户。

    距离的计算要用每个用户和所有的用户（除了他自己）都计算他们之间的距离，所以计算量也是很大的。

欧式距离计算方法：def  sim_distance(prefs, person1, person2)

from math import sqrt

# Returns a distance-based similarity score for person1 and person2
def sim_distance(prefs,person1,person2):
  # Get the list of shared_items
  si={}
  for item in prefs[person1]: 
    if item in prefs[person2]: si[item]=1

  # if they have no ratings in common, return 0
  if len(si)==0: return 0

  # Add up the squares of all the differences
  sum_of_squares=sum([pow(prefs[person1][item]-prefs[person2][item],2) 
                      for item in prefs[person1] if item in prefs[person2]])

皮尔逊相关系数计算方法： def sim_pearson(prefs,p1,p2)

# Returns the Pearson correlation coefficient for p1 and p2
def sim_pearson(prefs,p1,p2):
  # Get the list of mutually rated items
  si={}
  for item in prefs[p1]: 
    if item in prefs[p2]: si[item]=1

  # if they are no ratings in common, return 0
  if len(si)==0: return 0

  # Sum calculations
  n=len(si)
  
  # Sums of all the preferences
  sum1=sum([prefs[p1][it] for it in si])
  sum2=sum([prefs[p2][it] for it in si])
  
  # Sums of the squares
  sum1Sq=sum([pow(prefs[p1][it],2) for it in si])
  sum2Sq=sum([pow(prefs[p2][it],2) for it in si])	
  
  # Sum of the products
  pSum=sum([prefs[p1][it]*prefs[p2][it] for it in si])
  
  # Calculate r (Pearson score)
  num=pSum-(sum1*sum2/n)
  den=sqrt((sum1Sq-pow(sum1,2)/n)*(sum2Sq-pow(sum2,2)/n))
  if den==0: return 0

  r=num/den

  return r

    3. 寻找最相似的TopN相似用户 

    其实就是利用相似性计算函数sim_xxx来获得对这个用户的topN相似用户，排序，去top N个用户。

    选择是皮尔逊相关系数评价函数来计算相似度，它可以消除”夸大分值“所带来的影响。

    在这个例子里，量纲都是一致的，所以两种评价方法都是适用的。

# Returns the best matches for person from the prefs dictionary. 
# Number of results and similarity function are optional params.
def topMatches(prefs,person,n=5,similarity=sim_pearson):
  scores=[(similarity(prefs,person,other),other) 
                  for other in prefs if other!=person]
  scores.sort()
  scores.reverse()
  return scores[0:n]

    4.推荐电影

     直接推荐给相似用户一个对方没看过的电影，未免有点太随意了。

     我们须要通过一个经过加权的评价值来为影片打分， 评论者的评分结果因此而形成了先后的排名。为此，我们须要取得所有其他评论者的评价结果， 借此得到相似度后，再乘以他们为每部影片所给的评价值。

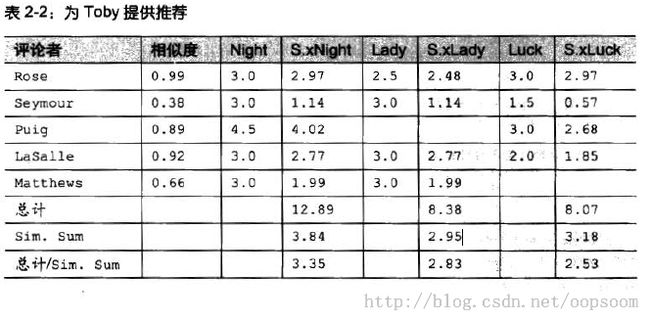
     下图中是Toby这个人匹配出来的相似的用户，最匹配的有Rose，LaSalle...... 且这个矩阵是稀疏的。

     Night，Lady，Luck是三部电影。每个用户对每个电影的打分，S.xNight,，S.xLady，S.xLuck是 total = 相似度 × 对电影的打分的结果。

     可以看出，越是相似度高的，得到的s.x的得分就比较高。所以相似用户的的相似度综合sim.sum =sum(各个用户sim值). 

     最后score = total / sim.sum

     得到最后的评价分数，然后依据这个分数排序，来对Toby进行推荐。

     可以看到Night这个电影可以推荐给Toby。

     注：这里有个问题，为什么不用total来计算分值呢? 是因为矩阵是稀疏的，这样对那些稀疏的向量是不公平的。

     即Puig没有看过Lady这个电影，也就无从评价相似度了。所以用total / sum(sim)比较公平。

      

     代码见：

# Gets recommendations for a person by using a weighted average
# of every other user's rankings
def getRecommendations(prefs,person,similarity=sim_pearson):
  totals={}
  simSums={}
  for other in prefs:
    # don't compare me to myself
    if other==person: continue
    sim=similarity(prefs,person,other)

    # ignore scores of zero or lower
    if sim<=0: continue
    for item in prefs[other]:
	    
      # only score movies I haven't seen yet
      if item not in prefs[person] or prefs[person][item]==0:
        # Similarity * Score
        totals.setdefault(item,0)
        totals[item]+=prefs[other][item]*sim
        # Sum of similarities
        simSums.setdefault(item,0)
        simSums[item]+=sim

  # Create the normalized list
  rankings=[(total/simSums[item],item) for item,total in totals.items()]

  # Return the sorted list
  rankings.sort()
  rankings.reverse()
  return rankings

好了，到此，就是一个简单的推荐系统，可以指定特定的人，来向他推荐电影了。唯一所做的是要维护这个偏好数据字典。

3.2为某部电影推荐相似电影

    假设我们想了解哪些商品是彼此临近的，该如何做呢？

    其实就是计算2个item的相似度，在这里是依据用户的打分，计算2个电影的相似度。实现方法其实是一样的，只要将偏好字典的key换成电影名称就可以了。

{'Lisa Rose': ('Lady in the Water': 2.5, ' Sna)ces on a Plane': 3.5) ,
' Gene Seymour ': { 'Lady in the Wa ter ': 3.0, 'Snakes on a Plane': 3.5}}
换成
{'Lady in t he Water' :{'Lisa Rose':2.5, 'Gene Seymour':3.0} ,
'Snakes on a Plane' :{'Li sa Rose' : 3 .5 , 'Gene Seymour':3.5}} etc..

我们可以写一个方法，将文章开头提到的数据集转换一下格式。

def transformPrefs(prefs):
  result={}
  for person in prefs:
    for item in prefs[person]:
      result.setdefault(item,{})
      
      # Flip item and person
      result[item][person]=prefs[person][item]
  return result

4. item-based CF 基于物品的协同过滤

    Know limitations： 现在的电子商务网站如Amazon千百万的用户，将一个用户和其它用户比较，然后再对每位用户评过分的用户比较，速度太慢。

这个矩阵会很大很大，而且很稀疏很稀疏，这让用户间的相似度比较很难。

    在大数据的情况下，基于物品的协同过滤比基于用户的协同过滤效果好很多，基于物品的协同过滤能将大量的计算任务放到预处理，而不必放到推荐过程中，从而是推荐系统的效率提升。

    基于物品的过程沿用了我们之前已经讨论过的许多内容。其总体思路就是为每件物品预先计算好最为相近的其他物品。然后，当我们想为某位用户提供推荐时，就可以查看他曾经评过分的物品.并从中选出排位靠前者，再构造出一个加权列袭，其中包含了与这些选中物品最为相近的其他物品。此处最为显著的区别在子，尽管第一步要求我们检查所有的数据，但是物品间的比较不会像用户间的比较那么频繁变化。这意味着.无须不停地计算与每样物品最为相近的其他物品，我们可以将这样的运算任务安排在网络流量不是很大的时候进行，或者在独立于主应用之外的另一台计算机上单独进行。

    可以理解为，用户间相似度的计算是频繁变化的，用户的口味一直在变，而物品的相似度是大致稳定的。

    1. 获取偏好，以物品为key，用户对该物品的打分为value.   eg:   item1 ,{user1: 3, user2 : 5}

    2. 相似度函数选取

    3. 评价打分，取TopN相似

    4. 加权推荐。

def calculateSimilarItems(prefs,n=10):
  # Create a dictionary of items showing which other items they
  # are most similar to.
  result={}
  # Invert the preference matrix to be item-centric
  itemPrefs=transformPrefs(prefs)
  c=0
  for item in itemPrefs:
    # Status updates for large datasets
    c+=1
    if c%100==0: print "%d / %d" % (c,len(itemPrefs))
    # Find the most similar items to this one
    scores=topMatches(itemPrefs,item,n=n,similarity=sim_distance)
    result[item]=scores
  return result

计算结果：

>>> reload(recommendations)
<module 'recommendations' from 'recommendations.py'>
>>> itemsim = recommendations.calculateSimilarItems(recommendations.critics)
>>> itemsim
{'Snakes on a Plane': [(0.2222222222222222, 'Lady in the Water'), (0.18181818181818182, 'The Night Listener'), (0.14285714285714285, 'Superman Returns'), (0.09523809523809523, 'Just My Luck'), (0.0425531914893617, 'You, Me and Dupree')], 'Lady in the Water': [(0.4, 'You, Me and Dupree'), (0.2857142857142857, 'The Night Listener'), (0.2222222222222222, 'Snakes on a Plane'), (0.2222222222222222, 'Just My Luck'), (0.09090909090909091, 'Superman Returns')], 'Just My Luck': [(0.2222222222222222, 'Lady in the Water'), (0.15384615384615385, 'You, Me and Dupree'), (0.15384615384615385, 'The Night Listener'), (0.09523809523809523, 'Snakes ona Plane'), (0.05128205128205128, 'Superman Returns')], 'Superman Returns': [(0.14285714285714285, 'Snakes on a Plane'), (0.10256410256410256, 'The Night Listener'), (0.09090909090909091, 'Lady in the Water'), (0.05128205128205128, 'Just MyLuck'), (0.036036036036036036, 'You, Me and Dupree')], 'You, Me and Dupree': [(0.4, 'Lady in the Water'), (0.15384615384615385, 'Just My Luck'), (0.14814814814814814, 'The Night Listener'), (0.0425531914893617, 'Snakes on a Plane'), (0.036036036036036036, 'Superman Returns')], 'The Night Listener': [(0.2857142857142857, 'Lady in the Water'), (0.18181818181818182, 'Snakes on a Plane'), (0.15384615384615385, 'Just My Luck'), (0.14814814814814814, 'You, Me and Dupree'), (0.10256410256410256, 'Superman Returns')]}

可以看到每个 itemX : [ （sim1, item1），（sim2, item2） ] 

每个item相对于其它item的相似度计算出来了。 可以根据此表形成下列矩阵来进行推荐评价：

我们到底要给Toby推荐那几部他没看过的电影呢?  x 维度都是没看过的电影。

1. 电影Superman对Night的相似度是0.103，Toby对Superman的评分是4.0， 那么R.xNight =  4.0 × 0.103 = 0.412。

2. total = sum(R.xItemX.......)

3. sim.sum = sum(sim)

4. score = total / sim.sum  即1.378 / 0.433 = 3.183 得出来Night的评分。

代码：

def getRecommendedItems(prefs,itemMatch,user):
  userRatings=prefs[user]
  scores={}
  totalSim={}
  # Loop over items rated by this user
  for (item,rating) in userRatings.items( ):

    # Loop over items similar to this one
    for (similarity,item2) in itemMatch[item]:

      # Ignore if this user has already rated this item
      if item2 in userRatings: continue
      # Weighted sum of rating times similarity
      scores.setdefault(item2,0)
      scores[item2]+=similarity*rating
      # Sum of all the similarities
      totalSim.setdefault(item2,0)
      totalSim[item2]+=similarity

  # Divide each total score by total weighting to get an average
  rankings=[(score/totalSim[item],item) for item,score in scores.items( )]

  # Return the rankings from highest to lowest
  rankings.sort( )
  rankings.reverse( )
  return rankings

5. 选择

    针对当前大数据环境，生成推荐列表时，item-based cf 明显比 user-based cf要快，不过它的确有维护物品相似度袤的额外开销。同时，这种方格根据数据集"稀疏"程度上
的不同也存在精F程度上的差异.在涉及电影的例子中，由于每个评论者几乎对每部影片都做过评价，所以数据集是警集的(而非稀疏的).另一方面，它又不同于查找两位有相近
del.icio.us 书签的用户一一大多数书签都是为小众群体所收藏的，这就形成了一个稀疏数据集。对于稀疏数据集，基于物品的过滤方法通常要优于基于用户的过施方法，而对于密集数据集而宫，两者的效果则几乎是一样的。

6.总结：

    基于用户的协同过滤比较容易实现，而且无需额外步骤，比较适合数据量较小的并且变化非常频繁的内存数据集。

    基于物品的协同过滤在大数据环境下显然速度要比基于用户的协同过滤要快，因为它不再运行时生成推荐列表，而是可以预处理物品之间的相似值计算，比较稳定。

参考文献：<<collective intelligence>>

Ps:

   本文如有不正确之处，请指出，小弟感激不尽。

   原创文章，转载注明出处自：http://blog.csdn.net/oopsoom/article/details/25389285 不枉我码了那么久的字。。。

-EOF-