Mining Massive Datasets课程笔记(三)
Communities in Social networks
Community Detection in Graphs
The Affiliation Graph Model(AGM)
Plan:
1. 由给定的模型生成网络
2. 对给定的网络找到“best”model
Model of network
Goal:Define a model that can generate networks
这个model将有一系列的参数,后续需要估计和检测community
问题是:给定一系列节点后,communities是如何产生network的边的呢?
这里我们讨论的模型就称为Community-Affiliation Graph Model它是图的生成模型。如下图:
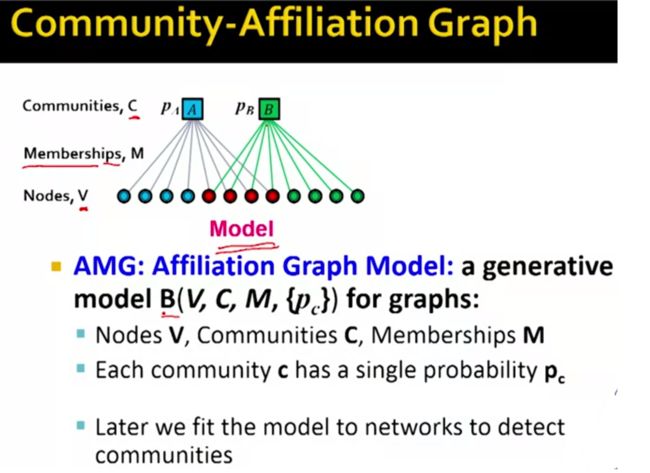
回到我们的plan计划项中第一条,我们如何根据这个AGM模型生成network呢?
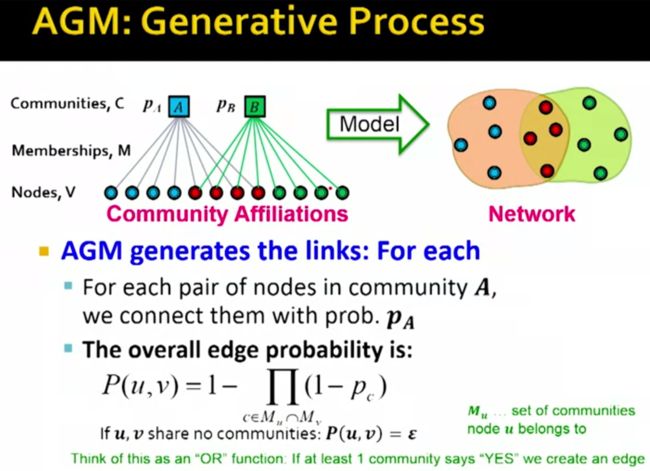
由AGM模型的式子可以看出,只要两个节点在某一个共同的Community中有边,则认为这两个节点之间是边的。
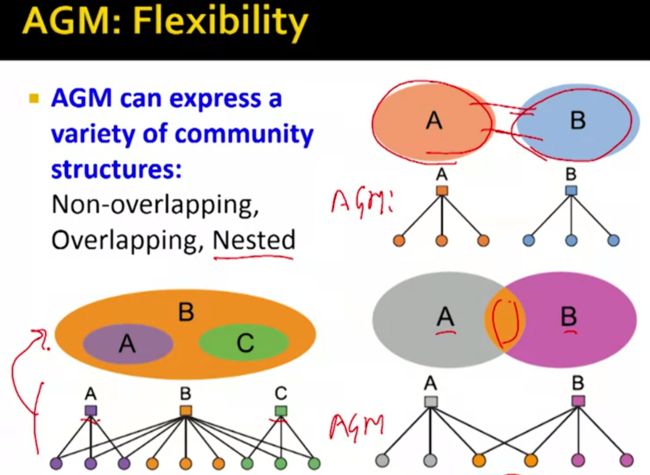
下面这张slide表明了AGM模型的灵活性
From AGM toBigCLAM
前面AGM模型中节点要么是某个Community的成员要么不是,即要么要边要么没有边,下面我们讨论的是如果edge表示的不仅仅是成员从属关系,而是成员在这个Community中的活跃度之类的信息,那么边的值就是一个>=0的值,等于0表示不是其成员,其它>0的值是一个degree。
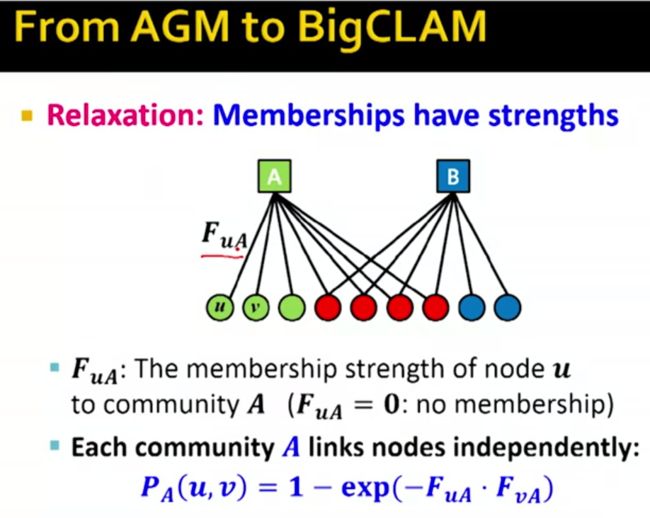
对于一个特定的Community A ,A中的两个节点u,v 之间有联系的概率计算如上图所示,不难理解其意义,如果两个节点都的degree in A都接近0,即都和Community A 的联系不紧密,那么上式结果也近似为0,那么这两者之间有联系的概率也很小,degree都接近1时反之。
上面讨论的是两个节点只共同出现在一个CommunityA里面,那么如果两个节点分在多个不同的Community都有重合呢
为了解决这个问题我们首先要介绍Community Membership Strength matrix F
如下图左边是matrix F,行表示各个节点,列表示Community

和AGM类似,两个节点间有link的概率也是至少有一个Community C links these nodes的概率。于是有

Solving The BIGCLAM
BigCLAM:How to Find F
有前面我们已经知道如果已知matrix F,求network的边的概率是可行的,
那么如何获得这个矩阵F呢?

这里使用的是极大似然估计,通常我们采用取对数的极大似然函数。

通俗来说就是找到参数F使得获得的网络图形尽可能类似于给定的网络图G。根据参数F我们知道可以获得一个网络图,这个网络图恰好就是给定的G的概率如上式argmax…因此求得这个概率的极大值即为估计的F矩阵。使用梯度上升法求极大值。

上式中每一次迭代都需要计算所有的节点,因此很浪费时间,改进如下:

Detecting Communities as Clusters
我去,手贱了一下把写好的东西都弄没了,还没上传,那这部分就直接总结大意好了,反正Week3的东西总体都很好理解。
What Makes a good Cluster?

一个good cluster,它内部的connection要尽可能多,与外界的联系要尽可能少。因此我们定义了一个Graph Cut的概念。
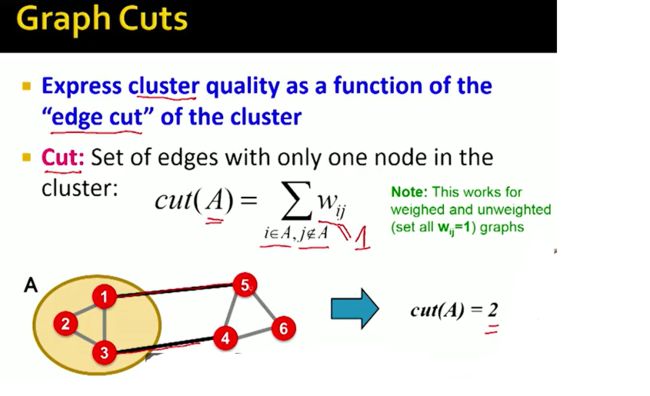
Cut指的是有且只有一个点在clusterA中的边,如图中黑色边
那么Cut score也就可以代表cluster quality中一个重要的部分了。即上张图中minimum的部分,即与外界的联系尽可能少。
但是单纯使用Cut score还不够,原因如下图最右边的绿色节点划分问题。
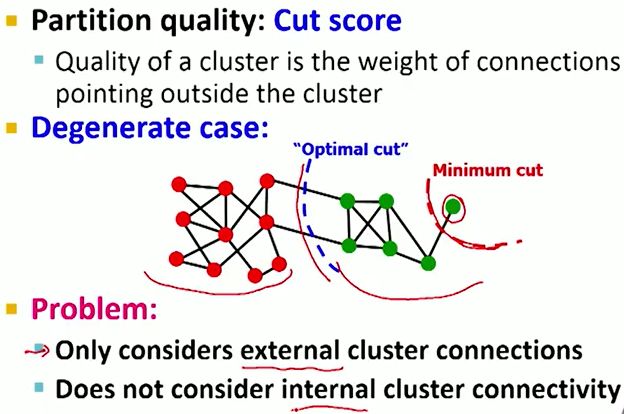
因此我们需要在此基础上进行改进。
如上图, ϕ(A)=Cut(A)Vol(A) 。分母指的是将V划分为clusterA和Cluster(V-A)后,较小的那个sets中所有节点的度的和。
ϕ(A) 越小,则cluster划分得越好。
Example:

Spectral Graph Partitioning
参考链接2中有图谱论的简单介绍,参考链接4中具体写了拉普拉斯矩阵和谱聚类。这里既然是写课程笔记就不展开了, 建议先看看这两个的内容。
一个无向图对应有一个对称的邻接矩阵,因而也有对应的实特征值(值的集合称作图的谱)
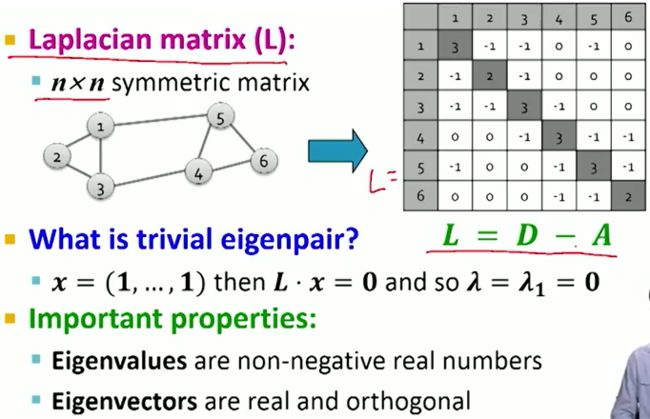
Graph Laplacian Matrix 拉普拉斯矩阵
拉普拉斯矩阵(Laplacian matrix)),也称为基尔霍夫矩阵, 是表示图的一种矩阵。给定一个有n个顶点的图G(V,E),其拉普拉斯矩阵被定义为:
L = D - A
其中D为图的度矩阵,A为图的邻接矩阵。
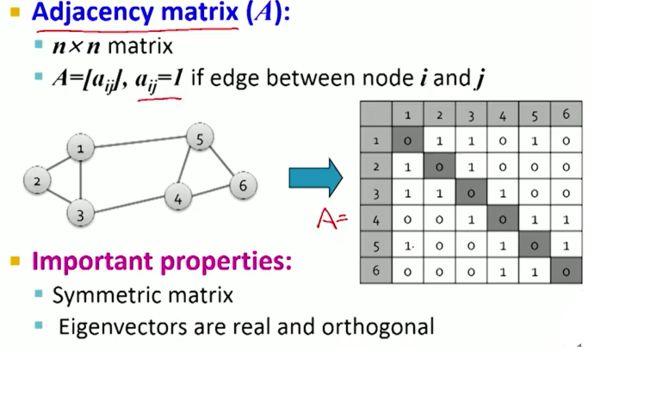
对于图G的邻接矩阵A中的元素 Aij,Aij=1 如果i,j之间有边,否则为0。
矩阵A是对称矩阵,A的特征向量都是实向量且为正交。

度矩阵是一个对角矩阵,对角上的元素就是对应行(列)的特征矩阵上的和。
因此拉普拉斯矩阵如下:
Spectral Graph Partitioning
介绍完几个矩阵后我们回到我们本来的意图上来,就是利用图谱进行图划分,即谱聚类。
首先我们如果要找optimal Cut来划分图的话,可以通过定义一个function如下使得这个分离策略造成的Cut score最小。

但是对于离散的点要求这个optimal Cut属于NP问题,所以我们不妨放宽条件松弛为连续的特征向量问题。这个就用到了前面说了那么长的拉普拉斯矩阵的特征向量啦,真的是很巧妙啊,那么为什么可以这么用呢?怎么用?巧妙在哪里呢?
首先要陈述这样一个事实:对于对称矩阵,它的次小特征值 λ2=minxxTMxxTx
那么对于图G, xTLx 有什么意义呢?

神奇的是 xTLx 可以化为上面的形式,另外,我们还知道对于x满足一下两个条件:
- x是unit vector,长度为1: ∑ix2i=1
- x和最小特征值0对应的特征向量(1,1,…1)正交: ∑ixi⋅1=∑ixi=0
因此,我们对于拉普拉斯矩阵有

我们图G上的点按照x label标注形成向量X(x1,…xn)后,通过获得次小的特征值 λ2 (因为 λ1=0 )就可以使得分离的代价函数最小,即为optimal Cut。
到这里我们就能明白前面所说的将离散问题转化为连续的求特征向量的问题了:

即图G的拉普拉斯矩阵L,在最小的非0特征值时对应的特征向量即为最合理的optimal Cut 的表示,这个向量又称为Fiedler向量,这个特征值称为谱间距(spectral gap)或Fielder value。剩下的仅是将松弛化的问题再离散化,即将特征向量再划分开,便可以得到相应的类别。
Spectral Clustering Algorithm
说了这么多下面总结下利用谱聚类算法将划分图时的步骤(3 steps):
- 预处理pre-processing
将图用矩阵表示:度矩阵,邻接矩阵,拉普拉斯矩阵 - 特征值分解decomposition
生成最小的k个特征值和对应的特征向量; - 分组Grouping
将特征向量聚类,然后划分类别,通常对2中产生的N*k的矩阵使用k-means算法进行聚类,从而划分k类;
划分方法可以有多种
在数值计算中,求矩阵的最大特征值,往往要比求最小特征值更方便和高效,因此也经常对拉普拉斯矩阵L进行归一化处理。参考文献6 2.4节,并且文章最后解释了为什么要大费周章使用拉普拉斯矩阵而不直接使用邻接矩阵。

——摘自参考文献5
Stream Algorithms
Mining Data Streams数据流挖掘
通常我们是利用数据库或者分布式文件系统中的数据进行数据挖掘,因此可以随时重复访问相同的数据。但要知道也有些数据是没有存在数据库中的如网络站点的web流量,或者是数据量太大以至于查询速度太慢如从卫星获取的数据等。因此需要更有效更好地方式来处理。这些数据都属于流数据。
The Stream Model
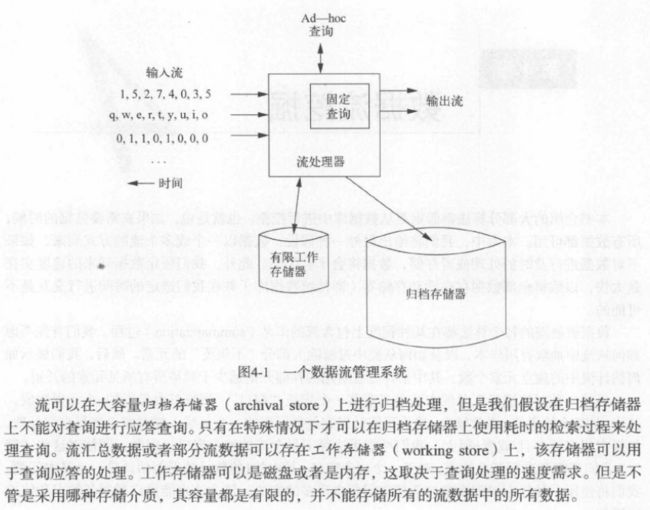
Data Management VS. Stream Management
流数据管理系统中数据的输入数据时由外界决定的,例如谷歌搜索每秒都有成千上网条搜索项,这个数目是由用户群决定的。而数据库管理系统中则由programming人员使用SQL输入。

若干数量的流进入流管理系统,每个流可以按照各自的时间表来提供元素,不同流的数据率或数据类型不必相同。
对于这种情况我们该如何利用有限的存储空间来获取流数据的信息呢。
首先介绍两种查询方式,Ad-hoc查询和固定查询:

总结:
Sliding Windows
滑窗中存储的是最近接受的N个输入数据,或者是在时间T内接受到的数据。存在问题是: 有可能N太大,导致内存存储不了,或者流太多,导致存储这些不同流的窗太多,内存存储不了。
看一个利用sliding windows进行查询的例子:

Counting 1‘s
这节讲的是流中的计数问题。将Stream看做一个二进制流,我们希望计算sliding windows N位中有几个1。我们比较关心的是内存中无法存储整个窗口的情况。
此时要精确计数是比较困难的,因此考虑近似估计。其实在海量数据挖掘中,近似处理的方法用的非常非常多,因为我们往往对小误差的容忍要大于时间或空间太大的容忍。
DGIM算法
Ref:
MMDS课程https://class.coursera.org/mmds-003/lecture
写图谱的博客http://blog.sina.com.cn/s/blog_439371b501012lgz.html
维基百科https://en.wikipedia.org/wiki/Spectral_graph_theory
July大神博客http://blog.csdn.net/v_july_v/article/details/40738211
http://lamda.nju.edu.cn/conf/MLA07/files/YuJ.pdf
谱聚类算法http://www.cnblogs.com/sparkwen/p/3155850.html
From:http://blog.csdn.net/sherrylml/article/details/49007899
