软考之路--计算机背后的故事
二十年过去了,今天她再次出现在我面前,还是一样的眼神,藏在记忆深处的“文法”跟眼前的这个“她”有什么不一样呢?在计算机科学中,文法是编译原理的基础,是描述一门程序设计语言和实现其编译器的方法。文法的描述多用BNF(巴克斯范式),而另一个重要的概念:正则表达式,也是文法的另一种形式。今天小编主要给大家讲解一下文法的相关知识。介绍文法的知识之前,先让我们来看一张图,小编会围绕这张图的内容展开,一一介绍。
好了,按照我们上面导图的顺序,小编一一来讲解一下各个知识点,还请各位大神不吝赐教。
终结符和非终结符
听着“终结”两个字儿,顿时感觉高大上的感觉,有么有,伴随着的是,这个是什么nie,都没有听说过,这是什么东东,其实这个并没有我们想象中的那么困难,首先,我们来看一个例子:

结合上面的例子,开讲啦,S为开始符,S,A,B为非终结符,在左边,可以推导出一个式子来。而p,q,a,b,c,d为终结符。讲到这里,小伙伴们是不是有点儿懵的感觉呢,什么终结符非终结符的,这个知识点我们可以这样来帮助我们来理解,我们可以这样想,S(start)也是一个非终结符,然后大写的为非终结符,小写的为终结符,那么这个概念就理解起来,也就没有那么困难了。
文法的类型
文法的类型,有四种,这类知识点,在软考中通查都会这样考察我们,让我们判断这几种文法的类型。
0型文法
结合下面的例子,我们来看看什么叫0型文法;
0型文法是这几个文法中,限制最少的一个,所以我们平常见到的至少是0型文法。G=(Vn,Vt,P,S),其中Vn是非终结符的集合,Vt是终结符的集合,P是推导式的一个集合,S是开始符。结合上面的例子,小编的分析如下:我们从图中来阐述一下这些概念,S,A,B为Vn,而p,q,a,b,c,d,为Vt,S为开始符。整个集合为P。我们每个式子里边的左边必须要包含这些元素或者元素组合中的至少一个非终结符,右边可以是这些元素的任意组合,左边有非终结符,右边有终结符,就欧了。如:A->ab。
1型文法
也叫上下文有关文法;这个1型文法理解起来也不是我们想象中的那么困难;在0型文法的基础上,我们再添加一点点的限制就行了,我们看添加了什么限制:右边的长度>=左边的长度,这个长度我们可以这样来理解,就是这些字符的数量,小的推出大的或者相等的。这样可以帮助我们理解。比如:A->B,A->Bba 都符合要求,那么反过来,Bba->A就不符合要求了,因为左边是3,右边是1。
2型文法
也叫上下文无关文法。2型文法在1型文法的基础上,我们规定2型文法中,左边必须是非终结符,然而一个终结符一个非终结符的组合不是一个非终结符,如Ab不是一个非终结符,但是两个非终结符的组合就是一个非终结符了,如AB就是行了。那么应该是这样的:aB->abc就不符合要求,但是AB->abc就符合要求了。
3型文法
也叫正规文法,对应有限状态自动机。在2型文法的基础上再加限制。要求更加高。要么一个非终结符推出一个终结符,要么一个非终结符推出一个终结符并且带一个非终结符。4个文法类的定义是逐渐增加限制的,因此每一种正规文法都是上下文无关的,每一种上下文无关文法都是上下文有关的,而每一种上下文有关文法都是0型文法。说了这么多的理论知识,接下来,我们来看一个问题:
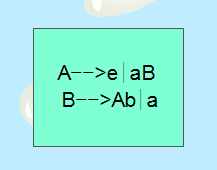
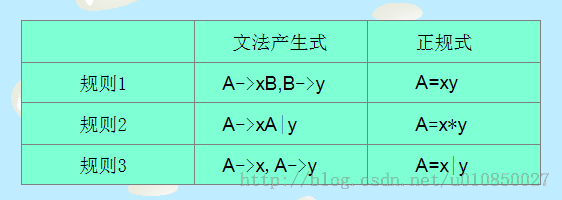
首先我们先把她拆开来写,A->e A->aB B->Ab B->a,接着,判断是否符合0型文法,0型文法规定左边必须有非终结符,符合,判断是否符合1型文法,1型文法是从小推到大的,也符合,判断是否符合2型文法,2型文法规定左边必须是非终结符,满足,最后,我们来看是否符合3型文法,3型文法只能符合右线性或者左线性,那么前面一个应该是符合右线性的,后面一个符合左线性的,所以综合起来看,不符合3型文法。所以,该题属于2型文法。接着,我们来讲解一下正规表达式。还记得当时敲机房收费系统的时候,有很多文本框,需要判断是否为空,写了一篇博文判断输入信息是否为空,米老师给了这样的评论,以后我们都采用正则表达式,那么正规表达式和正则表达式有什么不一样呢,点击相应的连接,或许对您有帮助`(*∩_∩*)′。今天我们主要来讲讲正规表达式和正规文法之间的转换,首先,我们来看下面这张表格:
结合上面的表格,我们来分析一下这些规则
规则1:文法产生式(A—>xB,B->y ),正规式(A=xy)。对于这个文法产生式转换成正规式,我理解的就是一个代入的过程,把B=y代入A->xB即可得出正规式。反过来,正规式转换成文法产生式,则添加一个变量就可以了了。 规则2:这个式子里边有一个递归,A—>xA,这样就产生递归了,应该是这样的:A->xA,A->xA……这样的无穷下去,最终A还是要等于y的,所以x就有无穷多个,从0个到无穷多个,所以这个推导出来的正规式就是A=x*y,表明x有无穷多个。规则3:A—>x,A->y。那么A=x|y,这个就明白了。A退出x或者y。
有穷自动机
NFA与DFA的定义:DFA:确定的有限自动机,M=(S,E,f,So,Z),我们来分析分析这个五元组:S是一个有限状态集合;E就是一个输入字符;f是一个SxE至S的映射;So:初态;Z:终态。我们来看看具体的例子,光是理论和概念的东西最不好理解,来看看例子吧:DFA=({S,A,B,C,f},{1,0},F,S,{f}),我们对照上面式子就能看的出来各个元素代表的意义,我们再来分析一遍:{S,A,B,C,f}是一个状态集合;{1,0}是输入字符;F是一个映射,S是初态,{f}是一个终态。那么我们接下来看这些映射:K(S,0)=B,K(S,1)=A,K(A,0)=f,K(A,1)=C,K(B,0)=C,K(B,1)=f,k(C,1)=f;我们根据这个流程,就有了这么一张图:
然后再看看NFA的定义:M=(S,E,f,So,Z) 这个五元组跟DFA的定义一样,在此不再赘述。
小编寄语:第一次接触编译原理的相关知识,小编理解的不是很深入,该博文主要介绍了文法,正规表达式有穷自动机,都是小编在现阶段理解的一丢丢的皮毛,希赛视频看下来,也是晕头转向,一篇漆黑的感觉,总结完编译原理的相关知识后,对这块的内容的理解仍然不深,不为别的,该博文,只为记录一个单纯的过程,还有我走过的软考之路,未完待续......