通过木块砌墙题目体会动态规划算法
木块砌墙题目:
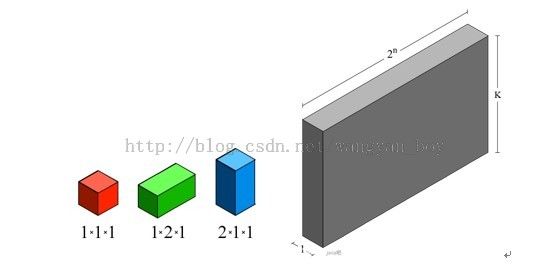
用三种木块,搭建k×2n×1的墙,不能翻转、旋转木块(0≤ n≤ 1024 ,1 ≤ k ≤ 5),计算有多少种方案,输出结果对1000000007取模。
图1 木块与墙
该题目是在庞果网(http://hero.pongo.cn/)第一次看到,但是由于该网站的特殊之处,现在看不到了,不过可以在这看到http://tieba.baidu.com/p/2351476089。
在解题之前,首先感谢庞果网的热心网友们的激情讨论,才让我的思路渐渐清晰成熟起来。
- 分析
看到n可以取值1024,即21024,这是一个很庞大的数字,一般不会也不可能计算出该数据再做处理,正常的思路是要想办法减低问题规模,并找出大规模问题与小规模问题之间的关系。该题目可以采用动态规划算法,将原问题递归划分为子问题,依据边界条件计算出子问题的解,然后根据子问题的状态及子问题之间的状态转移关系组合出原问题解。
墙与木块的厚度都为1,则可以只考虑宽度和高度(k×2n),进一步降低思考的难度。假设该问题结果用F(n,k)表示,由题目可知墙的宽度随着n增加1而增加一倍,所以降低n则可以快速降低问题规模。若能够找出最优子结构满足F(n,k) = g(F(n-1,k)); g()为子问题根据状态即状态转移关系合并子问题的策略。
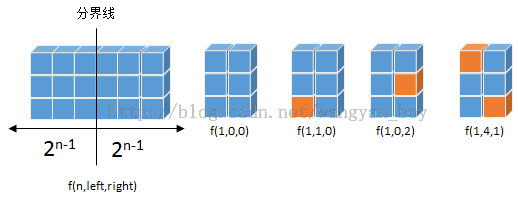
为了精确描述子问题,采用f(n,left,right)来表示不同状态的子问题(如下图所示)。由于木块宽度最大为2,所以只有相邻的两列才可能有联系,由上图也可以看出,相邻两列最多有2k种联系,即相邻子问题合并时有2k状态及相应的转移操作,f(n,left,right) =∑f(n-1,left,i)*f(n-1,i,right) 。
但是子问题规模降低到足够小,即n=0时到达边界,这是种比较特殊的子问题,需要特殊处理:
n=0时,问题退化为只有一列,此时结果只与k有关,假设结果为h(k),若k增加1:
第k+1个木块独立存在时,共有h(k)种方案
第k+1个木块与第k个木块组个存在时,有h(k-1)种方案
所以h(k+1) = h(k) + h(k-1)种方案,即h(k)为斐波那契数列。
n=1也是比较特殊的子问题。比如,f(1,4,1)= f(0,4,4)*f(0,1,1)+f(0,6,6)*f(0,3,3),如下图所示:
左右两边的状态实质上是两列之间有1*2的木块,方便描述和计算才给这些被1*2木块占据的位置编号作为子问题的状态,左右状态发生变化只能在没有被占据的位置上增加,如上图中f(1,4,1)的左状态由4增加时只能增加到6,而不能是5,右状态也是如此,只能增加到3。具体细节请看代码实现。
- 编程
#include <iostream>
using namespace std;
#ifdef WIN32
#define ll __int64
#else
#define ll long long
#endif
const unsigned long MOD = 1000000007;
//斐波那契数列求解函数
unsigned long fb(int k){
switch(k){
case 0:
case 1:return 1;
case 2:return 2;
case 3:return 3;
default:
unsigned long a = 2;
unsigned long b = 3;
unsigned long sum;
for(int index=3;index!=k;++index){
sum = a+b;
a = b;
b = sum;
}
return sum;
}
}
unsigned long calculate(int n,int k){
//子问题n=0时,结果退化为斐波那契额数列,特殊处理
if(0 == n){
return fb(k);
}
long top = 1<<k;
//申请辅助空间,保存子问题结果
ll ***res = new ll**[n+1];
for(int i=0;i<n+1;++i){
res[i] = new ll*[top];
for(int j=0;j<top;++j){
res[i][j] = new ll[top];
}
}
//初始化子问题n=0时的结果。
//n=0时,子问题只有一列,没有左右两半,这里采用了一个技巧,将左右两半看做一样,所以初始化就少了很多。
for(int i=0;i!=top;++i){
switch(i){
case 0: res[0][i][i] = fb(k); break;
case 1: res[0][i][i] = fb(k-1); break;
case 2:
case 3:res[0][i][i] = fb(k-2);break;
case 4:res[0][i][i] = 2*fb(k-3);break;
case 5:
case 6:
case 7:res[0][i][i] = fb(k-3);break;
case 8:res[0][i][i] = 3*fb(k-4);break;
case 9:res[0][i][i] = 2*fb(k-4);break;
case 10:
case 11:res[0][i][i] = fb(k-4);break;
case 12:res[0][i][i] = 2*fb(k-4);break;
case 13:
case 14:
case 15:res[0][i][i] = fb(k-4);break;
default:break;
}
}
//处理子问题n=1,这个子问题也比较特殊,左右状态导致有n=0合并结果的特殊化
for(int left=0;left!=top;++left){
for(int right=left;right!=top;++right){
res[1][left][right] = 0;
for(int stat=0;stat!=top;++stat){
int tmp = stat -left + right;
if(((stat&left)== left) && ((tmp&right) == right)){
res[1][left][right]+= res[0][stat][stat]*res[0][tmp][tmp];
}
}
res[1][right][left] =res[1][left][right];
}
}
//处理正常子问题
for(int row=2;row!=(n+1);++row){
for(int left=0;left!=top;++left){
for(int right=left;right!=top;++right){
res[row][left][right]= 0;
for(int stat=0;stat!=top;++stat){
res[row][left][right]+= res[row-1][stat][right]*res[row-1][left][stat];
res[row][left][right]%= MOD;
}
res[row][right][left]= res[row][left][right];
}
}
}
//返回结果
return res[n][0][0];
}
int main() {
const int n[] = {0,32,65,105,207,311,425,579,999};
const int k[] = {1,2,4,3,4,4,2,4,1};
const int answer[] = {1,751648137,558333535,811740953,785867720,246173916,906082702,853581641,222787673};
int i;
bool flag = false;
for (i = 0; i < 9; ++i) {
if (calculate(n[i],k[i]) == answer[i]) {
flag = true;
}
else {
flag = false;
break;
}
}
if(flag){
cout<<"YES!\n";
}
else{
cout<<"NO\n";
cout<<"the test data"<<n[i]<<" "<<k[i]<<endl;
}
return 0;
}