【软考】原码、反码、补码和移码由来和转换
随着软考的进行,从看软考视频的时候就接触了原码、反码、补码和移码这些东西,感觉挺简单的,做题应该是没有问题的,但是最近当做题再次看到这个的时候想到自己只是会做题而已,不知道为什么要使用,原理是什么?上网查了一些资料,将问题整理如下:
数值在计算机中以是机器数的形式表示的,它使用二进制计数制。为什么使用二进制呢,因为电脑只认识0和1,当然原因是因为电子管使用高低电流脉冲来去表示1和0,这样CPU中数以万计的晶体管就会通过复杂的电路来去运算各种复杂的运算。
原码的由来:
计算机中表示形式为机器数,计算机只能识别0和1,使用的是二进制。 而在日常生活中人们是使用的是十进制,并且我们用的数值有正负之分。于是在计算机中就用一个数的最高位存放符号(0为正,1为负)。这就是机器数的原码了。
反码的由来:
有了数值的表示方法就可以对数进行算术运算,但是很快就发现用带符号位的原码进行乘除运算时结果正确,而在加减运算的时候就出现了问题,如下:假设字长为8bits
十进制 (1) 10 - (1)10 = (1)10 + (-1)10 = (0)10
二进制 (0 0000001)原 + (1 0000001)原 = (1 0000010)原 = ( -2 ) 显然不正确。
因为在两个整数的加法运算中是没有问题的,于是就发现问题出现在带符号位的负数身上。对除符号位外的其余各位逐位取反就产生了反码。反码的取值空间和原码相同且一一对应。下面是反码的减法运算:
(1)10 - (1)10 = (1)10 + (-1)10 = (0)10
(0 0000001)反 + (1 1111110)反 = (1 1111111)反 = ( -0 ) 有问题。
(1)10 - (2)10 = (1)10 + (-2)10 = (-1)10
(0 0000001)反 + (1 1111101)反 = (11111110)反 = (-1) 正确。
补码的由来:
看上面的运算,问题出现在(+0)和(-0)上,在人们的计算概念中零是没有正负之分的。
于是就引入了补码概念。
ps:负数的补码就是对反码加一,而正数的补码不变,正数的原码反码补码是一样的。在补码中用(-128)代替了(-0),这个是人为规定的,所以补码的表示范围为:
(-128~0~127)共256个。
注意:(-128)没有相对应的原码和反码, (-128) = (1 0000000) 补码的加减运算如下:
(1)10 - (1)10 = (1)10 + (-1)10 = (0)10
(0 0000001)补 + (1 1111111)补 = (0 0000000)补 = ( 0 ) 正确。
(1)10 - (2)10 = (1)10 + (-2)10 = (-1)10
(00000001)补 + (11111110)补 = (11111111)补 = (-1) 正确。
移码的由来:
用补码表示阶码的时候,当阶码无限小,产生了下溢的时候,阶码变成了0,那么这个浮点数的值变为了1。
而实际上这个数是无限接近于零的。那么我们就需要取出其中的 "-0“ 值作为机器零。
移码(又叫增码)一般用做浮点数的阶码,引入的目的是为了保证浮点数的机器码为全0。
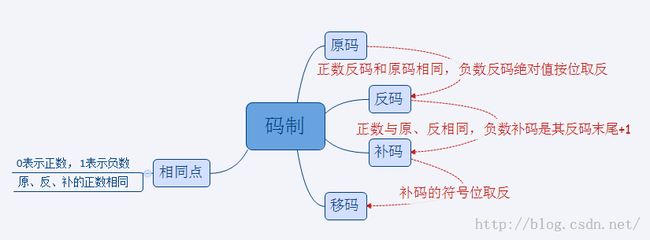
原码、反码、补码、移码之间的联系和区别:
小结:
(1)补码的设计使符号位能与有效值部分一起参加运算,从而简化运算规则。补码机器数中的符号位,并不是强加上去的,是数据本身的自然组成部分,可以正常地参与运算,并且使减法运算转换为加法运算,进一步简化计算机中运算器的线路设计。
(2)码制的所有这些转换都是在计算机的最底层进行的,而在我们使用的汇编、c等其他高级语言中使用的都是原码。
以上是很基础的总结,如有任何纰漏请指正,以上博客内容参考博客:http://indian.blog.163.com/blog/static/1088158200611853949863/