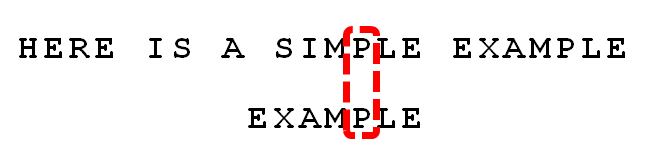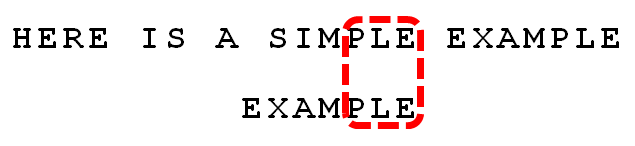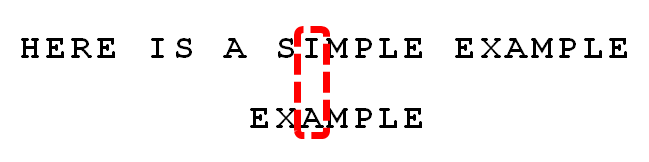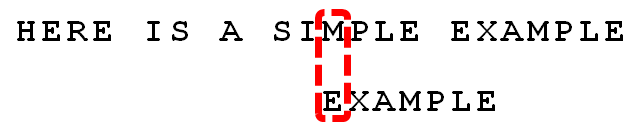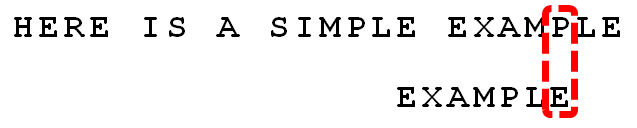大话数据结构十二:字符串的模式匹配(BM算法)
1. BM算法简介:
KMP算法其实并不是效率最高的字符串匹配算法,实际应用的并不多,各种文本编辑器的“查找”功能大多采用的是BM算法(Boyer Moore)。BM算法效率更高,更容易理解。
2. BM算法分析:
(1) 假定字符串为"HERE IS A SIMPLE EXAMPLE",搜索词为"EXAMPLE"。
(2) 首先,"字符串"与"搜索词"头部对齐,从尾部开始比较。这是一个很聪明的想法,因为如果尾部字符不匹配,那么只要一次比较,就可以知道前7个字符(整体上)肯定不是要找的结果。我们看到,"S"与"E"不匹配。这时,"S"就被称为"坏字符"(bad character),即不匹配的字符。我们还发现,"S"不包含在搜索词"EXAMPLE"之中,这意味着可以把搜索词直接移到"S"的后一位。
(3) 依然从尾部开始比较,发现"P"与"E"不匹配,所以"P"是"坏字符"。但是,"P"包含在搜索词"EXAMPLE"之中。所以,将搜索词后移两位,两个"P"对齐。
(4) 我们由此总结出"坏字符规则":
后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置值
如果"坏字符"不包含在搜索词之中,则上一次出现位置为 -1。
以"P"为例,它作为"坏字符",出现在搜索词的第6位(从0开始编号),在搜索词中的上一次出现位置为4,所以后移 6 - 4 = 2位。再以前面第二步的"S"为例,它出现在第6位,上一次出现位置是 -1(即未出现),则整个搜索词后移 6 - (-1) = 7位。
(5) 依然从尾部开始比较,"E"与"E"匹配。
(6) 比较前面一位,"LE"与"LE"匹配。
(7) 比较前面一位,"PLE"与"PLE"匹配。
(8) 比较前面一位,"MPLE"与"MPLE"匹配。我们把这种情况称为"好后缀"(good suffix),即所有尾部匹配的字符串。注意,"MPLE"、"PLE"、"LE"、"E"都是好后缀。
(9) 比较前一位,发现"I"与"A"不匹配。所以,"I"是"坏字符"。
(10) 根据"坏字符规则",此时搜索词应该后移 2 - (-1)= 3 位。问题是,此时有没有更好的移法?
(11) 我们知道,此时存在"好后缀"。所以,可以采用"好后缀规则":
后移位数 = 好后缀的位置 - 搜索词中的上一次出现位置
举例来说,如果字符串"ABCDAB"的后一个"AB"是"好后缀"。那么它的位置是5(从0开始计算,取最后的"B"的值),在"搜索词中的上一次出现位置"是1(第一个"B"的位置),所以后移 5 - 1 = 4位,前一个"AB"移到后一个"AB"的位置。
再举一个例子,如果字符串"ABCDEF"的"EF"是好后缀,则"EF"的位置是5 ,上一次出现的位置是 -1(即未出现),所以后移 5 - (-1) = 6位,即整个字符串移到"F"的后一位。这个规则回到上文的这个例子。此时,所有的"好后缀"(MPLE、PLE、LE、E)之中,只有"E"在"EXAMPLE"还出现在头部,所以后移 6 - 0 = 6位。有三个注意点:
(1)"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀,则它的位置以"F"为准,即5(从0开始计算)。
(2)如果"好后缀"在搜索词中只出现一次,则它的上一次出现位置为 -1。比如,"EF"在"ABCDEF"之中只出现一次,则它的上一次出现位置为-1(即未出现)。
(3)如果"好后缀"有多个,则除了最长的那个"好后缀",其他"好后缀"的上一次出现位置必须在头部。比如,假定"BABCDAB"的"好后缀"是"DAB"、"AB"、"B",请问这时"好后缀"的上一次出现位置是什么?回答是,此时采用的好后缀是"B",它的上一次出现位置是头部,即第0位。这个规则也可以这样表达:如果最长的那个"好后缀"只出现一次,则可以把搜索词改写成如下形式进行位置计算"(DA)BABCDAB",即虚拟加入最前面的"DA"。
回到上文的这个例子。此时,所有的"好后缀"(MPLE、PLE、LE、E)之中,只有"E"在"EXAMPLE"还出现在头部,所以后移 6 - 0 = 6位。
(12) 可以看到,"坏字符规则"只能移3位,"好后缀规则"可以移6位。所以,Boyer-Moore算法的基本思想是,每次后移这两个规则之中的较大值。更巧妙的是,这两个规则的移动位数,只与搜索词有关,与原字符串无关。因此,可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时,只要查表比较一下就可以了。
(13) 继续从尾部开始比较,"P"与"E"不匹配,因此"P"是"坏字符"。根据"坏字符规则",后移 6 - 4 = 2位。
(14) 从尾部开始逐位比较,发现全部匹配,于是搜索结束。如果还要继续查找(即找出全部匹配),则根据"好后缀规则",后移 6 - 0 = 6位,即头部的"E"移到尾部的"E"的位置。
3. BM算法Java实现:
public class BM {
final static int CARD_CHAR_SET = 256;// 字符集规模
/*
* @param mainStr 主串
* @param subStr 模式串
*/
public static int getMatchIndex(String mainStr, String subStr) {
int[] BC = BuildBC(subStr); // 坏字符表
int[] GS = BuildGS(subStr); // 好后缀表
// 查找匹配
int i = 0; // 模式串相对于主串的起始位置(初始时与主串左对齐)
while (mainStr.length() - subStr.length() >= i) { // 在到达最右端前,不断右移模式串
int j = subStr.length() - 1; // 从模式串最末尾的字符开始
while (subStr.charAt(j) == mainStr.charAt(i + j))
if (0 > --j) // 自右向左比较
break;
if (0 > j) // 若最大匹配后缀 == 整个模式串(说明已经完全匹配)
break;
else
i += MAX(GS[j], j - BC[mainStr.charAt(i + j)]);// 在位移量BC和GS之间选择大者,相应地移动模式串
}
return (i);
}
/*
* 构造Bad Charactor Shift表BC[] - 坏字符表
*/
protected static int[] BuildBC(String subStr) {
int[] BC = new int[CARD_CHAR_SET]; // 初始化坏字符表
int j;
for (j = 0; j < CARD_CHAR_SET; j++)
BC[j] = -1; // 首先假设该字符没有在P中出现
for (j = 0; j < subStr.length(); j++) // 自左向右迭代:更新各字符的BC[]值
BC[subStr.charAt(j)] = j;
return (BC);
}
/*
* 构造Good Suffix Shift表GS[] - 好后缀表
*/
protected static int[] BuildGS(String subStr) {
int m = subStr.length();
int[] SS = ComputeSuffixSize(subStr); // 计算各字符对应的最长匹配后缀长度
int[] GS = new int[m]; // Good Suffix Index
int j;
for (j = 0; j < m; j++)
GS[j] = m;
int i = 0;
for (j = m - 1; j >= -1; j--)
if (-1 == j || j + 1 == SS[j]) // 若定义SS[-1] = 0,则可统一为:if (j+1 == SS[j])
for (; i < m - j - 1; i++)
if (GS[i] == m)
GS[i] = m - j - 1;
for (j = 0; j < m - 1; j++)
GS[m - SS[j] - 1] = m - j - 1;
return (GS);
}
/*
* 计算P的各前缀与P的各后缀的最大匹配长度
*/
protected static int[] ComputeSuffixSize(String subStr) {
int m = subStr.length();
int[] SS = new int[m];// Suffix Size Table
int s, t; // 子串P[s+1, ..., t]与后缀P[m+s-t, ..., m-1]匹配
int j; // 当前字符的位置
SS[m - 1] = m; // 对最后一个字符而言,与之匹配的最长后缀就是整个P串
s = m - 1; // 从倒数第二个字符起,自右向左扫描P,依次计算出SS[]其余各项
t = m - 2;
for (j = m - 2; j >= 0; j--) {
if ((j > s) && (j - s > SS[(m - 1 - t) + j]))
SS[j] = SS[(m - 1 - t) + j];
else {
t = j; // 与后缀匹配之子串的终点,就是当前字符
s = MIN(s, j); // 与后缀匹配之子串的起点
while ((0 <= s) && (subStr.charAt(s) == subStr.charAt((m - 1 - t) + s)))
s--;
SS[j] = t - s;// 与后缀匹配之最长子串的长度
}
}
return (SS);
}
protected static int MAX(int a, int b) {
return (a > b) ? a : b;
}
protected static int MIN(int a, int b) {
return (a < b) ? a : b;
}
// 测试类
public static void main(String[] args) {
String mainStr = "HERE IS A SIMPLE EXAMPLE";
String subStr = "EXAMPLE";
System.out.println("字符串匹配的位置为: " + getMatchIndex(mainStr, subStr));
}
}
4. BF,KMP,BM算法比较:
(1) BF,KMP算法移动模式串的时候是从左到右,进行比较的时候也是是从左到右的。BM算法移动模式串的时候是从左到右,而进行比较的时候是从右到左的。
(2) 算法效率: BM算法 > KMP算法 > BF算法
5. BM算法参考资料:
(1) 阮一峰的博客: 字符串匹配的Boyer-Moore算法
(2) 淘宝搜索技术博客:字符串匹配的那些事