〖数学算法〗求圆周率的几种算法

圆周率大家都不陌生，最早由欧几里德《几何原本》中提到圆周率是常数，第一个用寻求圆周率数值的人是阿基米德，中国数学家刘徽，和后来大名鼎鼎的祖冲之分别对圆周率进行了计算，从古到今对圆周率的计算方法有几十种。

下面就介绍几种求圆周率的方法：

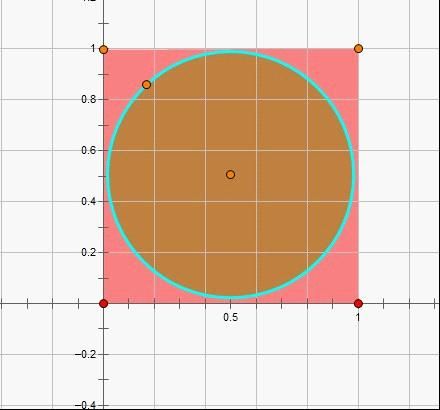
1.随机投点法（蒙特卡洛算法）

 这是粗略的求圆周率一种常用算法

在（0，0）和（1，1）范围内随机投test_sum个点，如果落到圆内，hit_sum数量加1，最后用hit_sum/test_sum算出落在圆内的概率，

由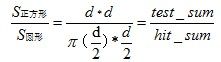得圆周率 PI=hit_sum / test_sum * 4

public class PI {

	public static void main(String[] args) {
		int test_sum = 1000000;// 投的点数
		int hit_sum = 0;// 投中的个数
		double x, y;// x和y坐标点
		for (int i = 0; i < test_sum; i++) {
			// 随机得到一个坐标
			x = Math.random();
			y = Math.random();

			if (x * x + y * y <= 1)// 判断掷入的这个点在不在在圆内
				hit_sum++;
		}
		// 统计得到π的值
		double pi = (double) hit_sum / test_sum * 4;
		System.out.println("π的结果为：" + pi);
	}
}

随机测试的几次结果：

π的结果为：3.140336

π的结果为：3.141012

π的结果为：3.141396

2.公式法

圆周率的公式特别多，介绍其中一个

这是一个迭代过程，code很容易，直接贴代码了

public class PI {
	

	public static void main(String[] args) {
		
	double my_pi = 2;
	int _jingdu = 1000;//精度控制
	for (int i = _jingdu; i > 0; i--) 
		my_pi = my_pi * i / (2 * i + 1) + 2;
	System.out.println(my_pi);
	
	}
}

输出结果：3.141592653589793

3.蒲丰投针

这一方法的步骤是：

　　1） 取一张白纸，在上面画上许多条间距为d的平行线。

　　2） 取一根长度为l（l<d） 的针，随机地向画有平行直线的纸上掷n次，观察针与直线相交的次数，记为m

　　3）计算针与直线相交的概率．

　　18世纪，法国数学家蒲丰和勒可莱尔提出的“投针问题”，记载于布丰1777年出版的著作中：“在平面上画有一组间距为d的平行线，将一根长度为l（l<d）的针任意掷在这个平面上，求此针与平行线中任一条相交的概率。”布丰本人证明了，这个概率是 p=2l/（πd)  π为圆周率。

这个方法真是不可思议，感兴趣的朋友可以模拟一下。

证明：http://files.cnblogs.com/ysjxw/蒲丰投针与蒙特卡洛模拟.pdf

福利：四行代码计算圆周率800位的怪异程序

#include 
#include 
int a=10000, b, c=2800, d, e, f[2801], g; 
main() 
{ 
for(;b-c;) 
f[b++]=a/5; 
for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a) 
for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b); 
return 0; 
} 

ps： LZ是看不懂它在干什么

我的第一篇博文写完啦，叹口气

==================================================================================================

  作者：nash_  欢迎转载，与人分享是进步的源泉！

  转载请保留原文地址：http://blog.csdn.net/nash_/article/details/8199357

===================================================================================================