棋盘覆盖问题
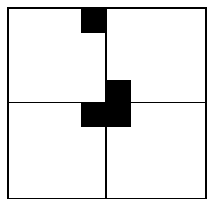
在一个 2^k * 2^k 个方格组成的棋盘中,若恰有一个方格与其它方格不同,则称该方格为一特殊方格,称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对任何 k>=0 ,有 4^k 种不同的特殊棋盘。下图所示的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。
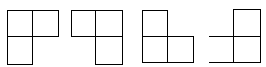
在棋盘覆盖问题中,要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格,且任何 2 个 L 型骨牌不得重叠覆盖。易知,在任何一个 2^k * 2^k 的棋盘中,用到的 L 型骨牌个数恰为 (4^k-1)/3 。
用分治策略,可以设计解棋盘问题的一个简捷的算法。
当 k>0 时,将 2^k * 2^k 棋盘分割为 4 个 2^(k-1) * 2^(k-1) 子棋盘,如下图所示。
特殊方格必位于 4 个较小子棋盘之一中,其余 3 个子棋盘中无特殊方格。为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘,我们可以用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处,如下图所示,这 3 个子棋盘上被 L 型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将原问题化为 4 个较小规模的棋盘覆盖问题。递归的使用 这种分割,直至棋盘简化为 1x1 棋盘。
对于上面图一的示例,棋盘覆盖效果如下:
c++代码如下:
#include<iostream> using namespace std; int tile=1; //L型骨牌的编号(递增) int board[100][100]; //棋盘 /***************************************************** * 递归方式实现棋盘覆盖算法 * 输入参数: * tr--当前棋盘左上角的行号 * tc--当前棋盘左上角的列号 * dr--当前特殊方格所在的行号 * dc--当前特殊方格所在的列号 * size:当前棋盘的:2^k *****************************************************/ void chessBoard ( int tr, int tc, int dr, int dc, int size ) { if ( size==1 ) //棋盘方格大小为1,说明递归到最里层 return; int t=tile++; //每次递增1 int s=size/2; //棋盘中间的行、列号(相等的) //检查特殊方块是否在左上角子棋盘中 if ( dr<tr+s && dc<tc+s ) //在 chessBoard ( tr, tc, dr, dc, s ); else //不在,将该子棋盘右下角的方块视为特殊方块 { board[tr+s-1][tc+s-1]=t; chessBoard ( tr, tc, tr+s-1, tc+s-1, s ); } //检查特殊方块是否在右上角子棋盘中 if ( dr<tr+s && dc>=tc+s ) //在 chessBoard ( tr, tc+s, dr, dc, s ); else //不在,将该子棋盘左下角的方块视为特殊方块 { board[tr+s-1][tc+s]=t; chessBoard ( tr, tc+s, tr+s-1, tc+s, s ); } //检查特殊方块是否在左下角子棋盘中 if ( dr>=tr+s && dc<tc+s ) //在 chessBoard ( tr+s, tc, dr, dc, s ); else //不在,将该子棋盘右上角的方块视为特殊方块 { board[tr+s][tc+s-1]=t; chessBoard ( tr+s, tc, tr+s, tc+s-1, s ); } //检查特殊方块是否在右下角子棋盘中 if ( dr>=tr+s && dc>=tc+s ) //在 chessBoard ( tr+s, tc+s, dr, dc, s ); else //不在,将该子棋盘左上角的方块视为特殊方块 { board[tr+s][tc+s]=t; chessBoard ( tr+s, tc+s, tr+s, tc+s, s ); } } void main() { int size; cout<<"输入棋盘的size(大小必须是2的n次幂): "; cin>>size; int index_x,index_y; cout<<"输入特殊方格位置的坐标: "; cin>>index_x>>index_y; chessBoard ( 0,0,index_x,index_y,size ); for ( int i=0; i<size; i++ ) { for ( int j=0; j<size; j++ ) cout<<board[i][j]<<"/t"; cout<<endl; } }
对应程序效果如下:
参考文献:
1. 《算法设计与分析》 ------------------------------------------------------------------------- 王红梅编著 清华大学出版社
2. 棋盘覆盖算法 http://riddickbryant.javaeye.com/blog/559388
3. 棋盘覆盖问题原理及演示程序 http://www.cnblogs.com/lsxqw2004/archive/2008/10/16/1313086.html