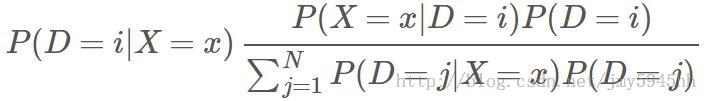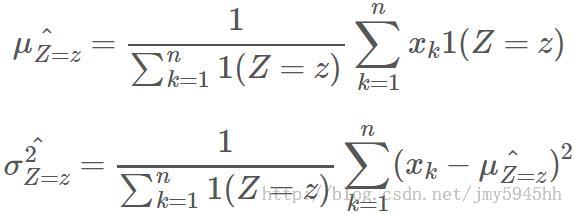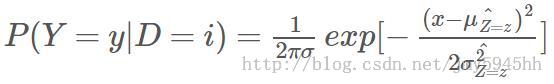In this latest #UberData installment, we bring you the data science details of how we use classic Bayesian statistics to solve a uniquely Uber problem.
One of the projects the #UberData Team worked on earlier this summer was determining which businesses Uber riders like to patronize. What kind of food? Which airports, which hotels? At first glance, this seemed simple enough: reverse geocode the dropoff coordinates, or use a publicly available database containing numerous urban addresses to match up to nearby businesses.
But soon we realized that the “nearby businesses” part was precisely the problem. In certain parts of San Francisco, and other dense urban areas like New York City, you can’t swing your handbag without hitting a restaurant. And just because you get dropped off in front of one doesn’t mean you’re going to it. During rush hour or at a busy intersection, we’re often willing to walk a few blocks to arrive at our final destination if this means avoiding a traffic jam or an extra red light.
在最近一期的#UberData中,我们展示了运用经典贝叶斯统计论来解决一个特定的Uber问题的数据技术细节。
这个初夏#UberData团队致力于研究的项目之一是发现哪个商家是用户最常光顾的。具体到,哪种食品店,哪些机场,哪些酒店。看起来问题似乎很简单:只需要逆向编码用户下车的地理位置坐标,或者是使用包含城市地址数据的公共数据库来匹配附近的商家即可。
但是很快我们就发现,“附近的商家”是棘手的问题。比如San Francisco的某些地区,或者NYC这样的高密度地区,你走在街晃晃手包就一定能碰上餐馆(随便走到哪儿都是餐馆)。这意味着,你在某家餐馆附近门口下车并不代表你要走进去。在交通的高峰时段或者某个繁忙的十字路口,相比于被车流以及红绿灯困在马路上,我们更愿意走路穿过几条街到达想去的地方。
As we introduce UberPool, the carpool option of our app, where drivers make multiple pickups and dropoffs, these occurrences will only happen with increasing frequency… which means that any Uber rider destination popularity analysis is susceptible to be inaccurate due to noise.
另外,我们引进了UberPool这个玩意儿,它是Uber APP中的拼车选项,使司机可以一趟在不同的地点多次上下客,这种情况发生的可能性只会越来越高……它导致所有针对Uber用户目的地偏好的分析都受到噪音的影响而更不准确。
What we need is information on where people ultimately want to go… rather than where people may specify where they want to be dropped off, in order to get there. Let’s build a probabilistic model that given dropoff latitude and longitude coordinates for a trip, predicts the address of the rider’s final destination.
我们需要的是用户最终想要去哪儿这个信息,而不是用户为了到某地,指明的下车地点。为此,我们建立了一个模型,输入是用户下车点的经度、纬度坐标值,输出是预测的用户最终想去的目的地。
In this post, we show you how Uber can use Bayesian statistics and where you get dropped off, to predict where you’re going 3 out of 4 times.
本节将展示Uber怎样利用贝叶斯统计理论以及用户的下车位置,在4次中3次(以75%的正确率)预测到您最终要去的地方。
Our Uber Data
所使用的Uber数据
We took the riding patterns of over 3000 unique riders in San Francisco earlier in 2014 (anonymizing the data to protect privacy.) Each of these trips had been “tagged” by the rider: when requesting an Uber, the rider had filled in the destination field. We assumed that this represented the true destination the rider wanted to go, creating a gold standard against which we can compare the predictions of our model.
我们提取了2014年初San Francisco地区3000多个独立用户的乘车数据(这些数据都已经匿名处理以保护隐私。)用户对他们的每次行程都“打上标签”:当他们通过Uber叫车时,就已经填好了目的地。我们假定这个目的地就是他们真正想去的地方,这为我们的预测模型提供了一个极好的对照标准。
Probabilistic Prediction
概率预测
Each address is a discrete indexed unit i=1…N . The goal of our model is to accurately predict the address i that the trip ends at given a previous point along the trip (dropoff), the time of the trip, and other characteristics of the rider and landscape.
Since the model is probabilistic, this involves calculating the probability of each address i being the trip’s final destination, P(D=i|X=x) , where D is a random variable representing the final destination and X is a random variable representing observed features of the trip.
每个地址都是被离散标号的值,i=1…N。我们模型的目标是准确预测行程的终点i,给定条件是行程中的某点、行程耗时以及某些用户和地理的特征描述。
这是一个概率模型,涉及到计算行每个可能地址i是某次行程终点的概率,即 P(D=i|X=x) , 其中D表示目的地随机变量,X表示已知的行程特征随机变量。
Separating this probability into a likelihood component and a prior component and applying Bayes’ Theorem gives
Here P(D=i) is the prior probability of the final destination being i , calculated as a weighted sum of assumptions, which we will lay out in the next section. P(D=i|X=x) is the likelihood of the final destination being i , having seen observed features X . This is computed from the distribution of distances between drop-off and final destination, as well the implications of time of trip.
将这个概率分解为似然概率部分和先验概率部分,运用贝叶斯理论,可得
其中 P(D=i) 表示目的地为i时的先验概率,它是通过对所有可能i值加权求和算出来的,具体会在下一节讲到。 P(D=i|X=x) 表示给定特征为X时,目的地为i的似然概率。它是通过下车点与最终目的地之间距离分布算出来的,其中也包括了行程发生的时刻这个因素。
Constructing the Prior
构建先验概率
Rider Prior
乘客先验
The rider prior PRider(D=i) incorporates useful information about a rider’s personal destinations into the model. The intuition is that individual riders are likely to go to certain addresses that other people are unlikely to go to (their house, their work place, etc.)
Thus what PRider(D=i) is really saying, is P(D=i|C=c) , where C is a random variable representing the identity of the rider. This distribution can be visualized as a histogram: each bar corresponds to a normalized number of times that rider c has been to address i .
乘客先验概率 PRider(D=i) 将关于用户个人的目的地有用信息包含了进去。直观的,每个用户常去的一些特定地方通常是其他用户不常去的(例如家、公司等)。
因此 PRider(D=i) 的意义实际上是 P(D=i|C=c) , 其中 C 是表示用户特征的随机变量。这个先验概率的分布可以用一个直方图表示:每条柱子对应着归一化的用户去地址i的次数。
Note that the Rider Prior assumes a closed world model: only the addresses that a rider has previously gone to are assigned any probability. (All other addresses have a probability of zero.)
This assumption, which is widely used in location-related algorithms, greatly simplifies things, but is obviously naive. In real life, people sometimes go to places they’ve never been before. More worryingly, the Rider Prior breaks down in the case of a new user. Locations must not only have been destined to; they must also have been observed. (So under this naive assumption, a new rider has zero probability of going anywhere!)
To address this conundrum we add 2 additional components to the prior: the Uber Prior and the Popular Place Prior.
用户先验假定的是一个“封闭世界模型”:只有用户曾经去过的地方被加入进去(其他地方去的先验概率都是0)
该假定常用于地理位置相关算法中,它极大的简化了问题,但缺点也是过于简单了。真实的生活中,人们偶尔会去他们从没去过的地方。更糟糕的是,对于新用户而言,用户先验完全失效。参与统计的地理位置不仅是用户去该去的,还必须是用户去过的。(因此在这个简单假设下,新用户去任何的地方的概率都是0!)
为了解决这个难题,我们给先验概率添加了额外的2个部分:Uber先验概率和热门地点先验概率。Uber Prior
Uber先验
The Uber prior PUber(D=i) takes a wider lens and exploits the fact that Uber riders, all together, are likely to go to certain places.
Uber先验 PUber(D=i) 将范围扩宽,把所有Uber用户去常去的地点考虑进来。
PRider(D=i)
PUber(D=i)=P(D=i|is Uber user) is the normalized number of times that any Uber Rider in the dataset has gone to address i .
PUber(D=i)=P(D=i|is Uber user) 是归一化的数据集中任意Uber用户去过地址i的次数。
Figure 1: The Uber Prior and a sample Rider Prior are mapped. Larger circle radii indicate that more trips in the training data were taken to that location.
图1:Uber先验和一个用户先验在地图上表示出来的效果图。越大的圆圈意味着训练集中更多人的去过该地。
Popular Place Prior
热门地点先验
With the Rider Prior and Uber Prior, we assume the only addresses in SF are the addresses frequented by riders in our dataset. This is clearly inaccurate. The Popular Place Prior is our “cover everything” prior, and is constructed with data using 1000 businesses that fit each of the following verticals in San Francisco well:
有了用户先验和Uber先验,目前我们的假设仅仅包含数据集中,常有用户去到的SF地点。显然这缺乏了精准性。热门地点先验是我们“覆盖一切”的先验,它根据SF地区,1000个较好符合下列条件的商家构建。
- restaurants 餐馆
- nightlife 夜场
- hotels 酒店
- shopping 商场
- museums 博物馆
- health 医疗保健
PPopular Place(D=i) is the normalized number of reviews left for a business establishment on the site.
PPopular Place(D=i) 是归一化的某个地点i处商家获得的点评数量。
Combining the Priors
将所有先验结合
Putting the 3 priors together allows for good coverage. The Rider Prior covers presumably the places you often go to. The Uber Prior covers the places your friends often go to (and in turn where you might go to, i.e., your friend’s house). The Popular Place Prior covers any other location of note.
Certain locations will be tracked in more than one prior and of course, there are locations that fall outside all 3 delineations. (The hope is that these are few and far between.)
把上述3个先验概率结合起来会有很好的覆盖率。用户先验覆盖了你常去的地方。Uber先验覆盖了你朋友常去的地方(它包括了例如说你朋友的家这样的地方)。热门地点先验覆盖了其他值得注意的地方。
某个地点可能被纳入多个先验概率中,也可能不处在任何一个先验概率中(希望这些少之又少)。
Currently we take α=.3 and β=.3 , we want to get a grasp on how each of the priors affects accuracy.
目前我们给定的系数是 α=.3 and β=.3 , ,希望能找出每个先验对最后结果准确性的影响程度。
Constructing the Likelihood
构造似然概率
Riders tend to be unwilling to be dropped off very far from their final destinations (see Figure 2 below). Intuitively, the farther away an address is from the drop-off, the less likely it is.
用户倾向于在离目的地不远的地方下车(见图2)。换句话说,离下车地越远的地方,用户越不可能去。
Figure 2: The distribution of distance between dropoff and final destination. The red vertical line indicates the 80th percentile.
图2:用户下车点与目的地距离分布图。红色竖线表示80%比。
We formalize this intuition with the likelihood: P(Y=y|D=i) . Y is the observations of Haversine distance between dropoffs and the final destination (essentially, the distance as the crow flies).
Now what does this likelihood look like? We model it using a Gaussian distribution N(μ,σ) , taking as μ and σ2 the maximum likelihood estimates μ^MLE and σ2^MLE .The MLE estimates for parameters of a gaussian are just the sample mean and sample variance of the data. Then P(Y=y|D=i)=N(Y=y|μ,σ2) .
我们用似然概率 P(Y=y|D=i)这个 数学语言来表征上述直观现象。Y表示下车点与最终目的地之间的迭加正弦距离值(实质上,距离是笔直的)。
注意到这个似然概率像什么(我注:高斯分布)?我们使用高斯分布N(μ,σ)建模,用μ和o作为最大似然估计值。MLE的高斯参数估计只需要样本均值和样本方差就行。可得 P(Y=y|D=i)=N(Y=y|μ,σ2) .
We also need to account for the type of neighborhood the dropoff is in. In a sketchy neighborhood, a rider might not want to walk even 50 meters, but in a busy downtown, dropoffs might be an approximate corner, in the general vicinity of where a rider is trying to ultimately go.
To capture this variance, we fit individual parameters for each zip code. That is,
我们也需要考虑到下车点附近区域的类型。在附近相对荒凉的地方,用户甚至不想走多50米,但是在市中心,下车点可能是附近的街角,也可能是最终目的地的附近大致位置。
为了把这个波动因素纳入考虑,我们对每个邮编区域使用独立的参数值,即:
Then a trip with observed dropoff-destination distance difference y in zipcode z will have the likelihood
那么一段行程中,邮编区域Z处的下车点和最终目的地的距离Y的似然概率如下:
The second part of the likelihood is temporal. Certain locations are more likely than others depending on the time of day and day of week. Commuting patterns imply that people will go to office buildings in the financial district of San Francisco in the morning and leave in the evening; night club trips are unlikely Monday morning, but restaurant trips are likely from 5-8 pm.
似然概率的第二个部分是时间因素。特定的地点会在某天的某个时间比其他地点更可能成为用户目的地。通勤路线意味着人们早上去到San Francisco的金融区,晚上离开;人们不太可能在周一早上到夜店去,去餐厅更可能发生在下午5-8点。
To model these tendencies, we use T as the random variable representing time of trip. P(T=t|D=i) is the probability of the final destination being i given that the time at dropoff is t . We specify P(T=t|D=i) as a categorical distribution with event probabilities calculated as a normalized count of trips taken to location i at time t . (The time increment we use is one hour.)
为了对这些倾向性建模,我们使用T作为行程发生的时间随机变量。 P(T=t|D=i) 表示给定时间为t的情况下,目的地为i的概率。我们规定上式为一个分类分布,事件的概率通过归一化的某个时间t到达i的行程总数计算。(时间以小时为跨度)
Inferring the Posterior
推测后验概率
In the previous sections, we introduced the prior and likelihood components. Multiplying these together gives us a number that is proportional to the posterior probability P(D=i|X=x) . Note in particular that we are making an independence assumption between the 2 components of the likelihood , that
在之前的章节中,我们介绍了先验概率和似然概率。把他们乘起来,就可以得到一个和后验概率P(D=i|X=x)成正比的数字。尤其注意,我们对两个似然概率的组成部分做了独立的假设,
P(X=x|D=i)=P(Y=y,T=t|D=i)=P(Y=y|D=i)P(T=t|D=i) .
This assumption is simplistic, since it is certainly possible that there is some interaction between Y and T . Basically, time could affect how far someone is willing to walk from their Uber to their final destination (but for now we assume this effect is minimal).
这是个极度简化的假设,由于很可能Y与T存在相互关联。大体的,时间会影响用户愿意从下车点走多远到最终目的地(目前我们假设这个影响非常小)。
Figure 3: An example posterior distribution for a correctly predicted test instance: 1348 Sacramento Street, San Francisco
图3:一个后验概率分布的例子,测试实例正确预测:1348 Sacramento street,SF
Results
结论
We evaluated our model using classic machine learning techniques, splitting the data into a test set and a training set to ensure our model was not tuned to just a specific set of trips in our dataset.
我们用传统的机器学习技术对模型进行了评估,将数据分为测试集和训练集,保证我们的模型不会偏向于某些特定的行程数据。
We iterated through each test trip, first outputting a candidate list of locations within 100 m of the dropoff. Then, we calculated the posterior probability of each of the candidates. We used the maximum a posteriori estimate (abbreviated as MAP): that is, we chose the address with the maximum posterior probability. We checked whether this address string matched the true address.
我们迭代了每条测试集中的行程,首先输出一个可能的地点列表,这些地方在下车点的100m以内。随后,我们计算出每个候选地点的后验概率。我们使用其中的最大后验概率:即,以最大后验概率的地址作为终值。最后,将这个终值与实际地点进行对比。
We found that 74% of the time, our model could correctly predict the exact address.
我们发现,该模型能够预测对74%的准确地址。
Think about the sheer number of possible businesses on a typical city street. About 3 out of every 4 times, we could correctly identify which of the numerous possibilities riders are headed — all with no additional information or context to go on.
试想下一个典型城市街道上商家的绝对数量。大概4次中有3次命中,我们可以正确的预测大部分用户的去向——所有这些还无需其他信息或者上下文支持。
We compared our model results against 2 baselines: the naive baseline, and the smart baseline. The naive baseline made a random choice among the candidate locations and achieved 40% accuracy. The smart baseline took the closest candidate location and achieved 44% accuracy. Thus, in the context of our alternatives of how we elect a final destination, our model results are a good start at determining where we help people get to in aggregate, but aren’t good enough yet for us to stop thinking about this type of problem.
我们将模型的效果与2个基准进行了比较:朴素基准、智能基准。朴素基准对候选地址进行随机选择,得到了40%正确率。智能基准选择就近地址,得到了44%正确率。因此,从这两个替代方案来讲,我们的模型对于决策用户的聚合情况开了个好头,但是我们还是得继续思考这类问题。
Where are we going next?
下一步做什么?
Our rider destination model is one way the #UberData Team is working on improving the Uber ride experience. Extensions of this project involve building more complex priors and likelihoods. For instance, one intuition is that people are likely to go to locations that are close to locations they frequent. (For instance, restaurants near their home, or subway stop near their workplace.) We could represent this with an additional prior specified as a bivariate gaussian.
In the interim, follow our #UberData Twitter stream or read more #UberData blog posts to learn more about what we’re up to.
我们的用户目的地预测模型是#UberData团队致力于提升用户体验的一个方法。后续的扩展包括建立更为深层的先验概率和似然概率。例如,直观的,用户更倾向于去常去的地方附近(像家附近的餐馆,公司附近的地铁站等)。我们可以用另外的二元高斯来表示这个先验概率。
现在而今眼目下,关注我们的#UberData Twitter stream或者#UberData blog posts以了解我们最新进展。
原文地址:http://blog.uber.com/passenger-destinations
译者:TITANIC上的小景
(完)