【趣题 一】--- 酒精与水问题
又是很久没更新博客了,上个月毕业季着实把人弄伤了,一篇博文都没写,这样下去肯定不是个好兆头。所以,为了督促自己坚持下去,保持一定的更新率,我又效仿67大神的方法,加入了一个新的系列--【趣题】。这个系列主要就是为了换换思维,每天沉浸在CSI、MIMO、AMC、Channel Capacity、Entropy、Diversity、Equalization这些单词所营造的氛围中,难免会失落与惆怅,产生一定的思维定势。今天是这个系列的第一篇,由于自己从小都有虎头蛇尾的传统,这个系列能保持多久,自己也没有太大把握,不过,尽力吧!哈哈~ 题目还是习惯用Latex来敲!
最后的两个容器里的浓度分别为多少呢?其实这个题本来就不难,就一般小学生都能算出来。那么这里的trick到底在哪呢?那就是这里不需要任何的复杂计算,需要的只是一点思考而已。首先给出的是“hammer-and-tongs” brute-force approach,也就是纯计算法。为了叙述方便我们为两个瓶子编上号:1号瓶--盛有体积为V的纯水,2号瓶--盛有体积为V的纯酒精。
Solution 1(Brute-Force): 当从1号瓶取Q体积的水倒入2号瓶中后,2号瓶酒精浓度变为![]() ,然后再把Q体积的酒水混合物倒回1号瓶,我们很容易知道,原来2号瓶中酒精浓度不变,依然为
,然后再把Q体积的酒水混合物倒回1号瓶,我们很容易知道,原来2号瓶中酒精浓度不变,依然为![]() 。关键是计算现在1号瓶中水的浓度从100%变为了多少?首先,1号瓶此时的总体积为V,酒精体积为
。关键是计算现在1号瓶中水的浓度从100%变为了多少?首先,1号瓶此时的总体积为V,酒精体积为 ,那么酒精的浓度就为
,那么酒精的浓度就为 ,所以水的浓度就为
,所以水的浓度就为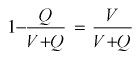 ,发现与2号瓶中酒精浓度一致。也就是说,经过上面这个过程后,“纯洁”的1、2号瓶受到了同等的“污染”,变为同等程度不“纯洁”的东西了。那么这里面有没有什么规律呢?或者说有没有一种elegant technique 不需要那么多计算呢?答案是肯定的,不然我还写这篇干嘛,【趣题】系列的“趣”就体现在这里,平时那么多计算早已厌倦了,心烦了,来点新鲜空气是必须的了!
,发现与2号瓶中酒精浓度一致。也就是说,经过上面这个过程后,“纯洁”的1、2号瓶受到了同等的“污染”,变为同等程度不“纯洁”的东西了。那么这里面有没有什么规律呢?或者说有没有一种elegant technique 不需要那么多计算呢?答案是肯定的,不然我还写这篇干嘛,【趣题】系列的“趣”就体现在这里,平时那么多计算早已厌倦了,心烦了,来点新鲜空气是必须的了!
Solution 2(Elegant-Beauty):我们知道当第一次操作后,也就是取了Q体积水倒入2号瓶后,2号瓶酒精的浓度就已经定了,为![]() ,这个答案容易得到。那1号瓶中水的浓度怎么解释呢?其实是这样的,我们从宏观上来看,最后的最后,两个瓶中的体积还是都为V,而2号瓶中的酒精浓度却降低了,这是为什么呢?那肯定是有一定体积的水置换掉了等体积的酒精,那置换掉的那部分酒精去哪了呢?它不可能跑到第三个瓶子中去,所以这部分酒精就跑到了1号瓶中。简而言之,1号瓶中用一定体积的水去“污染”2号瓶,2号瓶也还以颜色,以等量的酒精“污染”了1号瓶!而这里等量交换的体积即为
,这个答案容易得到。那1号瓶中水的浓度怎么解释呢?其实是这样的,我们从宏观上来看,最后的最后,两个瓶中的体积还是都为V,而2号瓶中的酒精浓度却降低了,这是为什么呢?那肯定是有一定体积的水置换掉了等体积的酒精,那置换掉的那部分酒精去哪了呢?它不可能跑到第三个瓶子中去,所以这部分酒精就跑到了1号瓶中。简而言之,1号瓶中用一定体积的水去“污染”2号瓶,2号瓶也还以颜色,以等量的酒精“污染”了1号瓶!而这里等量交换的体积即为 。所以,这道题还可以有一个变形题,即:
。所以,这道题还可以有一个变形题,即:
例-变形题:同样是有两个瓶子,分别盛有V体积的酒精与水,我们希望彼此互相交换M体积液体,请设计一种实现方式?
解:应该不用多说了吧,方法就是上面那道题的步骤,关键就是确定那个Q值,令 ,求解得出Q值。然后就按上题步骤进行,最后的结果就是实现了M体积的液体交换(怎么突然想到高中生物的 体液交换。。。囧)
,求解得出Q值。然后就按上题步骤进行,最后的结果就是实现了M体积的液体交换(怎么突然想到高中生物的 体液交换。。。囧)
总结一下这种Elegant方法的思想:面向对象而不是面向过程!原谅我用这么俗气的名字,但是确实有一定的联系。第一种粗暴的方法,是按照步骤一步步计算得来,需要清楚知道每一步到底发生了什么,这不就是面向过程编程的思想吗?而反观第二种方法,我们初始化了两个对象,酒精与水。这个对象具有两个属性:体积与浓度。具有方法:倒出液体。然后以对象这个整体来分析,对象开始都是纯净的,体积与浓度都被初始化了,两个倒出液体方法分别被调用后,我们看最后的结果,两个对象的体积属性没变,一个浓度已知,求另一个。(原谅我那么牵强的理解。。)
综述:当我们面对一个问题,想从它的过程来分析结果 十分复杂让你感到扑朔迷离(好比光子的跃迁),但它的部分结果状态已知时,我们就可以充分利用这些信息,来为我们的正确分析判断增加砝码。就好比通信里充分利用接收端信息来改善通信质量一样。
接下来想把问题推广下,可能会十分无聊,这个是前几天排队考科一(驾校问题可以列为那种过程十分复杂的那类,因为各种莫名其妙的事情都可能发生)时想了下,也不知道有没有意思。大概思路是这样的, 酒精与水这种混合可以看作是连续性问题,当我们关注的对象是离散的时,是不是也类似呢?
例-离散情况:同样是两个容器,分别装有5个绿球和红球,然后取两个绿球放入红球容器中混合,再从混合后的容器中取回两个放入绿球中,问绿球容器和红球容器中各自比例的期望值。
解:猜想各自比例就是5/(5+2)呀!这里V=5,Q=2而已。是不是这样的呢?我就无聊的算下吧。。对于红球容器中,最后的期望值为
而对于绿球容器有着同样的分析方法得出同样的答案,具有很好的对偶性!(请无视这么无聊的闲想,可能有错误!!)
希望今天开了个好头!
下期预告:要谈趣题,称硬币的题应该是最经典的了,【趣题 二】希望从信息论方面来谈谈这些题,或者一类题,能力有限,估计很难驾驭。
![]()

