Mining Massive Datasets课程笔记(五)聚类算法
Clustering
Overview of methods
首先我们说几个典型应用,了解为什么需要聚类算法,然后介绍下聚类的集中方法,具体的细节在后面的小节中详细说。

但是在实际应用中,聚类问题并没有图中这么简单,往往有大量的数据,且数据时高维的(10 or 10,000dimensions)处理起来比较复杂,而且在高维空间中点间的距离看起来都是近似的。
Some Clustering Applications
- clustering sky objects
- clustering CD’s
- clustering documents
聚类分析试图将相似对象归入同一簇,将不相似的对象归到不同簇。相似这一概念取决于所选的相似度计算方法,到底使用哪种相似度计算方法取决于具体应用。
Distance Measurement
对物品的不同表示方法,对应的距离度量方式也不同:

Overview:Methods of Clustering
- 层次法(Hierarchical)
- 凝聚式Agglomerative (bottom up)
每个点都初始化为一个“簇”,重复地将具有最近距离的两个簇合并成一个 - 分裂式Division (top down)
将整个分布作为一个簇,然后根据距离重复分裂为不同的簇
- 凝聚式Agglomerative (bottom up)
- 点分配法(Point Assignment)
保留一些列的簇,将点划分到距离最近的簇中。
层次聚类(Hierarchical Clustering)
我们主要讲凝聚式的层次聚类。仅适用于小型数据集。
主要操作:重复地将距离最近的簇进行合并操作。
因此,对于层次聚类算法,我们必须确定一下几个问题:
Three Problems:
- 簇如何表示?
- 如何选择进行合并的簇?
- 簇的合并操作合适停止(停止条件)?
首先我们从较简单的欧式空间讨论层次聚类问题,然后一一解答上面的问题。
欧式空间
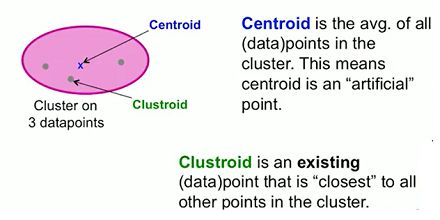
1. 在欧式空间中用质心(centroid)来表示簇,即簇中点的平均。
2. 计算簇的质心间的距离来表示簇间距离
3. 我们可以聚类到只剩一个簇为止,然而返回一个簇并没有实际意义,但是,合并的过程可以通过树形来表示,这种合并过程的表示往往具有很强的实际意义。当然,我们也可以通过实现指定簇的数目或者是指定最小确信距离等方法来确定停止条件。具体地后面讲解。
非欧式空间
在非欧式空间中,点集没有质心的概念,因此无法通过质心来表示cluster,因此我们从簇中选择一个点来代表簇,该点应该是距离簇内所有的点最近的点,称之为簇的中心(clustroid)。
然后簇间的距离计算和质心的距离计算一样,通过计算中心点间的距离来表示簇间距离。
那么我们如何来定义这个中心点呢?
我们说clustroid = point “closest” to other points. 那么我们如何定义这个closest呢?
选择中心点的方法,使得选出的点如下值最小 :
- 该点到簇中另外一点的最大距离(maximum)
- 该点到簇中其它各点的平均距离(avg)
- 该店到簇中其它各点的距离平方和(sum of squares)
前面我们已经讨论了前两个问题的解决,下面我们说第三条,也就是簇合并的停止条件如何确定。
停止条件(Termination Condition)
- 选择k个簇,当合并到k个时停止。前提是我们确信数据集的簇的数目。
- 如果在某个点时,现有簇的最佳合并会产生一个不恰当的簇时停止合并。i.e, a “bad” cluster.这里对于簇的好坏使用”cohesion“进行度量,当低于某个cohesion值时则认为是不恰当的簇。
Cohesion的定义
- 簇的直径:簇中任意两点之间的最大距离
我们可以设置为,当合并后的簇的直径大于某个阈值时,停止合并,半径同理。 - 簇的半径:簇中任意一点到质心(中心)的最大距离
- 基于密度的方法:簇的单位体积中点的数目。
当密度低于某个阈值时停止合并。
Implementation
定义两个簇的距离为两个簇中所有点对之间的平均距离,其中计算距离的两个点分别属于不同的簇。然后选取距离最近的合并。
时间复杂度为 O(N3)
使用优先队列进行优化后能减少到 O(N2logN)
这对于大数据集特别是内存存储不了的数据集而言,时间开销仍然太大,因此对于大数据集我们要采取新的方法。
K均值算法(The K-Means Algorithm )
我们假设是在欧式空间中使用欧式距离来度量。
首先我们需要确定类的数目k,然后创建k个点作为起始的簇的质心(通常是随机的选择)。
while(任意一个点的簇分配结果发生改变)do:
为每个点计算它的最近的质心,将其归为最近的那一簇。
计算完所有的点所属的簇后,更新k个簇的质心。
收敛条件是所有的点的分配不再发生改变,即质心稳定。
总体的流程很容易理解,那么这个k值我们应该如何选择,k个初始簇的质心如何确定呢?
Picking the right value for k
尝试不同的k值,观察随着k的增长,点到质心的平均距离的变化。
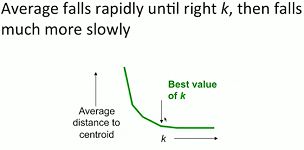
如果能够对不同的k下聚类结果的质量进行评价,我们就可以猜测到正确的k值。试想如果我们给定了合适的k值(甚至是更大的)那么簇的评价指标(如簇直径)将会上升的非常缓慢,但是,一旦k值小于真是数目,簇直径就会急剧增大,用图来表示如下:
Picking the initial k points
对于初始的k个簇,如何选择这k个质心呢:
- 采用层次聚类算法输出k个簇,在每个簇中选择离质心最近的点。
前面我们说到层次聚类仅适用于小型数据,因此我们首先需要对数据进行采样,采样后的数据能存入内存,然后对采样后的数据进行层次聚类,聚类到k类后选择质心。 选择彼此距离尽可能远的k个点。
首先随机挑选一个点while 挑选的点数目<k,do: 选择使该点到selected points们的最小距离尽可能大的点作为下一个selected point有点拗口,但很好懂,其实就是找最分散的k个点,这样的选择方式和初始的第一个点的选择关系比较大,会随着第一点的选择的不同而有所不同。
k均值的算法细节很简单,已经说完了,下面看复杂度:
虽然每一次计算点的分配情况以及重新计算质心只需要 O(kN)时间 ,但是由于需要迭代进行至收敛,因此时间消耗依然很长,我们能否找到一种类似的k均值算法,使得对数据的一次浏览就可以完成聚类呢?也就是我们下面要将的BFR算法,名词由来是三个发明这个算法的人(Bradley-Fayyad-Reina),适用于大型数据集。
BFR 算法
BFR算法时k均值算法的一个变形。BFR算法对簇的形状给出了一个非常强的假定,即它们必须满足以质心为期望的正态分布(Normally Distributed)。

一个簇在不同维度下的均值和标准差可能不同,但是维度之间必须相互独立 满足正态分布的假设说明每个簇看上去应该都是轴平行的椭圆形状。如下图绿色部分表示y维度上的标准差比较大,因此分布会沿y轴平行展开。

BFR Algorithm:Overview

我们说过BFR算法用来处理大型数据集,因此数据文件中的点按照组块的方式读入,如分布式文件系统中的chunk组块或者是传统文件分割后的小块。每个组块的数据必须保证能在内存中处理,即小于内存大小,因为内存中还要存储其它必要信息如:
既然废弃集或压缩集中的点不再存储,那么这个废弃集是如何表示这些点的信息的呢?
N-SUM-SUMSQ表示:
- 所表示的点的数目N
- 向量SUM:所有点在每一维的分量之和,即SUM[i]表示第i维上的分量和。
- 向量SUMSQ:所有点在每一维的分量的平方和。
因此,如果数据为d维的话,通过此方法可以用2d+1个值来表示一个废弃集或压缩集。而哦我们的实际目标是将一系列点表示为它们的数目、质心和每一维的标准差。根据N-SUM-SUMSQ表示,我们可以得到:
数据处理过程:
1. 首先找到所有“sufficiently close”充分接近某个簇质心的点加入到该簇中。加入新的点后,DS废弃集的调整计算通过N-SUM-SUMSQ表示很容易实现,直接加上这些新加入的点的 Ns,SUMs,SUMSQs 值即可。
2. 剩下得即是那些并不充分接近任一个簇质心的点。我们将这些点和之前的留存集中的点一起进行聚类(use any main-memory clustering algorithm)。将聚类的点概括表示并加入到压缩集CS中,剩余的单点簇则表示为点的留存集RS。
3. 通过第二步后,现在我们有了新的迷你簇,它们和上一个块的数据处理后留下的压缩集迷你簇和留存集中间可能距离很近是可以合并的。因此这一步就是将这些迷你簇和以前的压缩集的迷你簇和以前的留存集进行合并。
(如果这是最后一块数据了,那么就将这些留存集的点和压缩集分配到距离最近的簇中,否则继续保留压缩集和留存集,等待和下一块的数据一起处理。)
4. 分配给一个簇或迷你簇的点,即不再留存集中的点会和分配结果一起写出到二级存储器中。
虽然总体流程已经清楚了,但是我们不免对中间的实现细节有很多疑问:
如何确定某个新的点p距离某个簇足够近呢?如何界定这个”close enough“?
怎样界定两个压缩集是可以被合并的呢?
Q1:How Close is Close Enough?
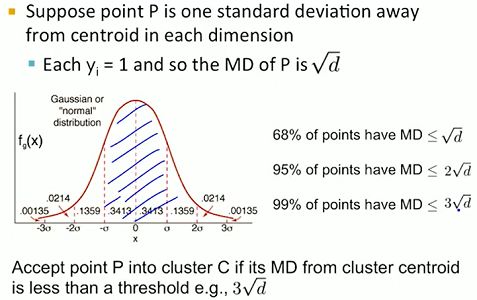
BFR approach:计算新的点p和每个簇质心的马氏距离(Mahalanobis Distance),我们选择具有最短马氏距离,且马氏距离小于某个阈值的簇加入。
马氏距离可以表示该点到该簇质心的概率。这一计算利用了最开始提到的BFR算法的前提假设:每个簇都是正态分布的点构成,且点的坐标和空间坐标保持一致。

Q2:Should 2 CS clusters be combined?
一种方式是计算两个cs clusters合并后的新的压缩集簇的方差,如果这个方差小于某个阈值则可以合并。
当然我们也可以选择其他方式,比如考虑新簇的密度等度量方式。
CURE算法
本节讨论另一个点分配类的大规模聚类算法CURE算法(Clustering Using Representatives),仍然假定运行在欧式空间下。BFR算法对簇的分布和形状都有很强的假设条件,因此在实际使用中有许多并不满足条件的聚类情况。而本节讨论的CURE算法不需要簇满足正态分布,更不需要符合轴平行,即对簇的形状没有任何假设。CURE算法使用一些代表点的集合来表示簇而不再是质心。
CURE算法初始化
CURE算法的完成
通过前面对每个簇生成代表点后,重新计算其它所有点到这些代表点的距离,将距离最近的分配到该簇中。(对数据的一次遍历就够了)
Ref:
https://class.coursera.org/mmds-003/lecture
《大数据:互联网大规模数据挖掘与分布式处理》
From:http://blog.csdn.net/sherrylml/article/details/49363509