2020李宏毅学习笔记——11.Unsupervised Learning： Linear Methods（无监督学习）

摘要

本章首先介绍了什么是无监督学习及无监督学习的类别，主要分类两种，一种是化繁为简型，如聚类复杂的input输入，简单的output输出，另一种是无中生有型，没有input x只有output y。接着，讲解了具有的聚类算法，常用方法有K-means和HAC，K-means主要思想是更新中心点来聚类，而HAC的思想是通过build a tree和选取阈值来实现的。其次通过聚类的不足，引入Dimension Reduction（降维）并详细展开 ,可以简单使用Feature Selection（特征选择）但是有的不能简单使用Feature Selection的方法，引入更好一点的方式，PCA（主成分分析法），详细讲解了PCA的原理与数学推导，以及PCA的应用。

1. Introduction（介绍）

无监督学习可以分为两大类：

第一类：化繁为简

• 聚类(Clustering)
• 降维(Dimension Reduction)

第二类：无中生有(Generation)

对于无监督学习(Unsupervised Learning)来说，我们通常只会拥有（x,y^）中的x或者y，其中：
化繁为简：把复杂的input变成比较简单的output，比如把一大堆没有打上label的树图片转变为一棵抽象的树，此时training data只有input x，而没有output y^。
无中生有：就是随机给function一个数字，它就会生成不同的图像，此时training data没有input x ，而只有output y^。

2.Clustering（聚类）

聚类，顾名思义，就是把相近的样本划分为同一类，比如对下面这些没有标签的image进行分类，手动打上cluster 1、cluster 2、cluster 3的标签，这个分类过程就是化繁为简的过程。

那我们怎么去确定分几个cluster呢 ？（通常是emperical 以实验为根据的）
聚类中最常用的方法有：
（1）k-means：a.随机初始化k个类的中心点；b.每个样本以最靠近的中心点的所属类为类标签；c.根据新得到的分类更新中心点；d.重复步骤b、c，直到模型收敛。
（2）Hierarchical Agglomeratiive clustering （HAC）层次聚类方法：根据样本之间的两两相似程度来建立一颗树；

2.1 K-means

该方法的大致过程如下：
a: 现有一大堆的unlabeled data {x1,x2,…,xn}，我们要把它划分为K个cluster
b: initial的时候可以从training data里随机挑K个object xn 出来作为K个center ci的初始值
c: 遍历所有的object xn ，并判断它属于哪一个cluster，如果xn与第i个cluster的center ci最接近，那它就属于该cluster
d:更新center：把每个cluster里的所有object取平均值作为新的center值
e:重复从c,d步骤，直到收敛

K-Means 算法思想较为简单如下所示：

1.选择K个点作为初始质心
2. repeat
将每个点指派到最近的质心，形成K个簇
重新计算每个簇的质心
3. until 簇不发生变化或达到最大迭代次数

2.2 HAC

假设现在我们有5个样本点，想要做clustering：

step 1：build a tree
整个过程类似建立Huffman Tree，只不过Huffman是依据词频，而HAC是依据相似度建树：

• 对5个样本点两两计算相似度，挑出最相似的一对，假设样本点1和2最相似
• 将样本点1和2进行merge (可以对两个vector取平均)，生成代表这两个样本点的新结点
• 此时只剩下4个结点，再重复上述步骤进行样本点的合并，直到只剩下一个root结点

step 2: pick a threshold
选取阈值，形象来说就是在构造好的tree上横着切一刀，相连的叶结点属于同一个cluster

上图中绿色的切割线，则可分为途中四类cluster。不同颜色的横线和叶结点上不同颜色的方框对应着切法与cluster的分法。

HAC和K-means最大的区别在于如何决定cluster的数量，在K-means里，K的值是要你直接决定的；而在HAC里，你并不需要直接决定分多少cluster，而是去决定这一刀切在树的哪里。

3. Dimension Reduction（降维）

clustering的缺点是以偏概全，它强迫每个object都要属于某个cluster，但实际上某个object可能拥有多种属性，或者多个cluster的特征，如果把它强制归为某个cluster，就会失去很多信息。所以我们应该用一个vector来描述该object，这个vector的每一维都代表object的某种属性。

如果将这种高维的vector（比如图像）转化成低维的vector，就叫做Dimension Reduction（降维）。

从另一个角度来看为什么Dimension Reduction可能是有用的！
左边是data以螺旋状分布在3维空间里。但其实如右边的样子，以2维的空间就可以描述这些信息，这样就把简化了问题。

再举一个具体的例子：
如果以MNIST(手写数字集)为例，每一张image都是$28\ast 28$的dimension，但我们反过来想，大多数$28\ast 28$ dimension的vector转成image，看起来都不会像是一个数字，所以描述数字所需要的dimension可能远比28*28要来得少。

举一个极端的例子，下面这几张表示“3”的image，我们完全可以用中间这张image旋转角度来描述，也就是说，我们只需要用这一个dimension就可以描述原先28*28 dimension的图像。

上例中只要抓住角度的变化就可以知道28维空间中的变化，这里的28维pixel就是之前提到的樊一翁的胡子，而1维的角度则是他的头，也就是去芜存菁，化繁为简的思想。

3.1 How to do Dimension Reduction？

在Dimension Reduction里，我们要找一个function，这个function的input是原始的x，output是经过降维之后的z。

做dimension reduction常用的方法是

• Feature selection（拿掉一些直观上就对结果没有影响的dimension）
• Principle component analysis(PCA)（主要成分分析）

3.2 PCA算法（Principle component analysis）

PCA认为降维就是一个很简单的linear function，它的input x和output z之间是linear transform，即z=Wx，PCA要做的，就是根据一大堆的x把W给找出来(现在还不知道z长什么样子)。

3.2.1 基于最大方差原理

1 . PCA for 1-D

为了简化问题，这里我们假设z是1维的vector，也就是把x投影到一维空间，此时w是一个row vector（行向量），z1=w1x，其中w1表示w的第一个row vector，假设w1的长度为1，此时z1就是x在w1方向上的投影。
那应该怎么去选w呢？
我们希望选这样一个w1，它使得x经过投影之后得到的z1分布越大越好，也就是说，经过这个投影后，不同样本点之间的区别，应该仍然是可以被看得出来的，即：

• 我们希望找一个投影的方向，它可以让投影后的variance越大越好
• 我们不希望投影使这些data point通通挤在一起，导致点与点之间的奇异度消失

上图中给出了所有样本点在两个不同的方向上投影之后的variance比较情况，要选择让样本在所投影到的维度上的方差尽量大。

2. PCA for n-D

投影到更高维的空间，对z=Wx来说：

• z1=w1x，表示x在w1方向上的投影
• z2=w2x，表示x在w2方向上的投影
• 同上
  

上图中 z1,z2,…串起来就得到z，而w1,w2分别是的第1,2,…个row，需要注意的是，此时W是一个单位正交矩阵，即（w1,w2,w3,…）相互正交，且都是单位向量。

那我们怎么去找w1,w2 呢？怎么解决这个问题？

数学公式推导
第一点：先来求解w1，把投影后z=w1·x的协方差矩阵写出来~

第二点：问题变成了求解带条件的最大值问题，采用拉格朗日乘数法求解~，可求得w1是x的协方差矩阵S的特征向量，且是最大特征值对应的特征向量。（线代矩阵运算）

第三点：依次往后退，w2是S的第二大特征值所对应的特征向量。

第四点：PCA达到的效果就是decorrelation（去关联），所以最后投影之后得到z的协方差矩阵D是对角矩阵。

• 投影矩阵W是单位正交矩阵
• W就是由x协方差矩阵S的特征向量组成
  

3.2.2 基于最小化误差原理

假设我们现在考虑的是手写数字识别，这些数字是由一些类似于笔画的basic component组成的，本质上就是一个vector，记做u1,u2,…，以MNIST为例，不同的笔画都是一个28×28的vector，把某几个vector加起来，就组成了一个28×28的digit
写成表达式就是：
其中x代表某张digit image中的pixel，它等于k个component的加权和加上所有image的平均值。

比如7就是x=u1+u3+u5，我们可以用来[ c1 c2 c3 … ck]T 表示一张digit image，如果component的数目k远比pixel的数目要小，那这个描述就是比较有效的。

实际上我们并不知道u1~uk具体的值，因此我们要找这样k个vector，使得之间越接近越好。

1. 基本思想：将x^近似看成是由多个u组成的，然后求解最小化它们之间的error时的系数c和分量u。

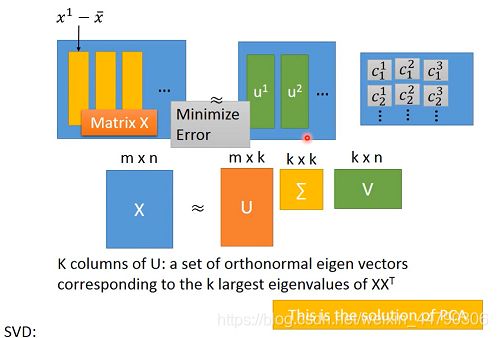
• 矩阵形式，Matrix X就是x^,用下图中的矩阵相乘来表示，我们的目标是使等号两侧矩阵之间的差距越小越好。
  
• 为了求解c和u（component），可以将X做奇异值分解SVD，用分解后的U代替u，ΣxV代替系数c，得到的U矩阵就是协方差矩阵XXT的k个特征向量。
  

3.2.3 从NN角度理解PCA

由于w之间时互相正交的，CK,也就是说c可以表示成(下图中）这两者的乘。PCA相当于只含一层hidden layer的AutoEncode，即具有一层隐含层的神经网络（线性激活函数），即输入和输出之间的误差越小越好。

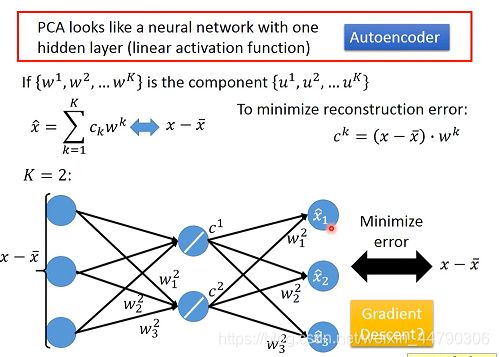
如果不是PCA的方法，只用neural network的解法不能够保证w之间是垂直的。但是如果用网络的话，可以用deep autoencode。（下一节会讲到）

3.2.4 Weakness of PCA

PCA有很明显的弱点：

• PCA是无监督的，不知道数据的标签，这样在降维映射之后可能会把两类数据混到一起。（考虑数据标签的方法LDA（Linear Discriminant Analysis）可以避免这一问题，但这属于监督学习）。
• PCA是线性的，把一个三维空间中的S形分布的数据做PCA之后的效果，就是把S形拍扁，而非展开。（对类似曲面空间的降维投影，需要用到non-linear transformation）
  

3.2.5 PCA for Pokemon（将PCA用于分析宝可梦的数据）

案例中800个宝可梦的cov(x)是6维，最多可以投影到6维空间，我们可以先找出6个特征向量和对应的特征值λi，其中λi表示第i个投影维度的variance有多大，计算6个特征值的ratio比重，舍去较小的（只取前四个特征值的特征向量作为新的特征，或者叫主成分PC）。（即特征值的意义是，PCA降维时，在相应维度的variance有多大。）

注意到新的维度本质上就是旧的维度的加权矢量和，下图给出了前4个维度的加权情况，从PC1到PC4这4个principle component都是6维度加权的vector，它们都可以被认为是某种组件，大多数的宝可梦都可以由这4种组件拼接而成，也就是用这4个6维的vector做linear combination的结果。

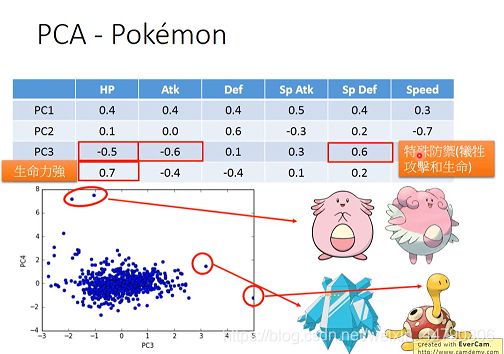
每个PC都是一个六维向量，分析它们在哪个维度是大的正值/负值，可以分析出这个PC所代表的意义。

3.2.6 PCA for MNIST

这个时候我们就可以熟练地把一张数字图像用多个组件(维度)表示出来了：
digit image = a1w1 + a2w2 + …，这里的wi就表示降维后的其中一个维度，同时也是一个组件，它是由原先28×28维进行加权求和的结果，因此wi也是一张28×28的图像，下图列出了通过PCA得到的前30个组件的形状：
在对MNIST和Face的PCA结果展示的时候，你可能会注意到我们找到的组件好像并不算是组件，比如MNIST找到的几乎是完整的数字雏形，而Face找到的也几乎是完整的人脸雏形，仔细思考了PCA的特性，就会发现得到这个结果是可能的，注意到linear combination的weight ai 可以是正的也可以是负的，因此我们可以通过把组件进行相加或相减来获得目标图像，这会导致你找出来的component不是基础的组件，但是通过这些组件的加加减减肯定可以获得基础的组件元素。

3.2.7 PCA和NMF比较

NMF：Non-negative Matrix Factorization，非负矩阵分解（这一节未细讲）

• NMF分解之后的component的系数都是正的，就拿image来说，也就是说分解之后的component像是原始image的一部分。
• PCA的系数可正可负，涉及到component的“加加减减”，而不是部分。

总结与展望

本章学习到了，无监督学习的种类，化繁为简型，包括聚类与降维，学习到了具体的聚类算法，K-means和HAC。HAC和K-means最大的区别在于如何决定cluster的数量，在K-means里，K的值是要你直接决定的；而在HAC里，你并不需要直接决定分多少cluster，而是去决定这一刀切在树的哪里。clustering的缺点是以偏概全，它强迫每个object都要属于某个cluster,我们应该用一个vector来描述该object，这个vector的每一维都代表object的某种属性,但有时候我们仅需要少量维度就可以表示是一个object。所以我们需要Dimension Reduction，我们可以使用feature selection和PCA等进行降维。其中PCA的应用更加广泛，但是PCA也有一些无法避免的缺陷。PCA与NMF有怎么样的区别与性能表现（自己去查阅补充）。下一节将会讲解降维算法(Dimension Reduction)的典型应用——词嵌入(word embedding)，以及如何用vector来表示一个word等，及相关应用。