计算24点问题

[-]

1. 递归方式
2. 递归方式的次数分析
3. 后缀表达式方法
4. 后缀表达式方法的一些细节
5. 后缀表达式方法的数值分析
6. 计算10以内1到10取4个数字用来算24点有多少种组合方式
7. 总结

说明：本文相关源代码在下面网址可下载：

http://download.csdn.net/detail/sun2043430/5223200

用4张扑克牌上的点数算24点是一个经典的游戏了。一般要求只允许使用加减乘除和括号进行四则运算。

例如：1,2,3,4   可以用表达式（1+2+3）*4 = 24 算出24。

如果用程序来实现的话有两种思路。

一是递归方式；一是后缀表达式（也称为逆波兰表达式）方法。

下面我们分别来介绍这两种方法。

一：递归方式

思路如下：

4个数字中任取2个数，使用一种运算得到一个数，将这个数和另外两个没有参与运算的数放在一起，这3个数再任取2个数进行运算，得到的结果再与另外一个数放在一起。

最后这两个数再进行运算，看结果是不是24，如果是，我们就找到了一个满足要求的表达式了。

根据这个思路，我们可以写递归函数如下：

RecursiveCalc（数组，数组长度 )

    取数组中2个数计算，和另外的数 组成新的数组

    递归调用RecursiveCalc（新数组，数组长度-1 )

递归到数组长度=1时结束，此时只需要看数组中元素是否=24，就可以知道这一次运算是否满足要求。

递归的原理是比较简单的，但是里面一些细节需要注意：

1. 取出来做运算的2个数应该是不同位置的两个数，例如我们在1,2,3,4中取了3，另外一个数就不能取3了。

2. 组成新数组的时候也要注意，是和没有参与运算的数组成新的数组。

3. 如果遇到了除法，要小心被除数=0的情况。

4. 因为除法可能会产生分数，所以运算中要采用浮点数，不能用整数。例如1,5,5,5 计算24点的表达式为（5 - 1/5)*5

   关于处理分数的情况，还有一种方法是 自己实现分数类，所有的数都用分数类对象表示。

5. 递归方式的打印输出很麻烦，因为到最后一个数是24的时候，你并不知道这个24是通过怎样的运算步骤得到的，所以需要保存中间运算步骤，以便最后的结果输出。

    在我实现的代码中，递归的输出部分也是写的比较垃圾，比较好的方式是每个数字都是一个对象的成员，参数用对象来传递，对象中保留表达式。

以下是我实现的递归函数代码：

bool RecursiveCalc(double *pArray, int nCount)
{
    bool bRet = false;
    if (1 == nCount)
    {
        if (fabs(pArray[0] - 24.0) < 0.0001)
        {
            g_Total++;
            Output(pArray[0]);
            return true;
        }
        else
            return false;
    }
    for (int i = 0; i < nCount; i++)
    {
        for (int j = 0; j < nCount; j++)
        {
            if (j == i)
            {
                continue;
            }
            double f1 = pArray[i];
            double f2 = pArray[j];
            char *p = g_op;
            for (int nop = 1; nop <= 4; nop++, p++)
            { 
                if ('/' == *p && fabs(f2) < 0.0001)
                { 
                    continue;
                }
                double f = Operation(f1, f2, *p);
                double *pnew = new double[nCount-1];
                if (!pnew)
                {
                    return bRet;
                }
                pnew[0] = f;
                for (int m = 1, n = 0; m < nCount-1; m++)
                { 
                    while (n == i || n == j)
                    {
                        n++;
                    }
                    pnew[m] = pArray[n++];
                }
                bRet |= RecursiveCalc(pnew, nCount-1);
                g_n2--;
                g_n1 -= 2;
                delete pnew;
                if (g_bOnlyGetOne && bRet)
                {
                    return true;
                }
            }
        }
    }
    return bRet;
}

二：递归方式的次数分析

在不考虑加法和乘法的交换律的情况下，对于给定的4个数字的递归算法有以下排列：

1. 4个数中取2个数的排列  12种 *4种运算符 = 48种
2. 3个数中取2个数的排列  6种  *4种运算符 = 24种
3. 2个数中取2个数的排列  2种  *4种运算符 = 8种

所以共有48*24*8种 = 9216种情况

   

三：后缀表达式方法

后缀表达式又称为逆波兰表达式，是一种把运算符放在要运算的两个数值后面的一种表示方法，后缀表达式的好处是可以不用括号。

例如对于（1-2）/(3-4)这样的表达式，后缀表示法为：12-34-/，在解释后缀表达式时，我们从左到右扫描，遇到运算符就往运算符的左边

取最近的两个数值进行运算，运算结束后将这个运算符和对应的两个运算数替换为运算结果，然后重复这个过程，直到算出最终结果。

例如对于3 ,6 5 - 8 + * 这个表达式，我们可以这样计算：

遇到数字先不管，遇到第一个符号是减号，往前找两个数，是6和5，所以就是6-5，结果=1。用1替换掉6 5 - 得到新的表达式：

3 1 8 + * 接下来是加号，1+8 = 9，表达式变为：3 9 *

最后的结果就是3*9 = 27。

而原来的表达式转换为我们平时看到的中缀表示法就是：3*（6-5+8），可以看出后缀表达式避免了括号。

关于这种表达式的更详细说明，读者可以搜索相关介绍。

接下来看看在4个数算24点中，如何构造后缀表达式，因为后缀表达式要求在一个符号前面必须要有2个操作数，所以对于4个数值（3个运算符），

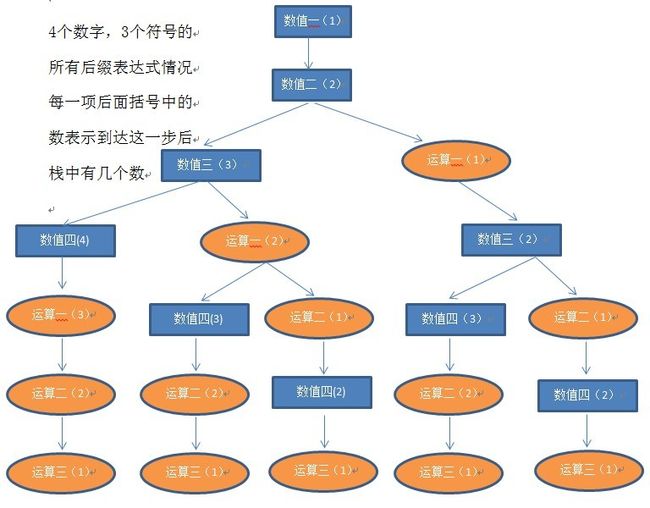
我们构造如下的树来表示所有可能的后缀表达式情况：

图中，从最上面开始往下构造合法的后缀表达式，蓝色方块表示加入的是数值，黄色椭圆表示加入的是运算符，注意后面括号中的数字，表示的是

当前表达式实际上等同于有几个数值。比如3 5 -这个表达式等同于一个数值，而3 5这个中间表达式表示有2个数值。

因为是4个数的所有组合，所以加入数值四之后就不再加入数值了，而且我们最后要得到一个结果（也就是一个数值），所以到达最后一步的时候，

整个表达式等同于1个数值。

将后缀表达式看成栈操作是很多教科书和文章中都提到的一种理解方式，其中向栈中加入数值时不进行任何处理，向栈中加入运算符则取栈顶的2个

操作数和运算符进行运算，运算结果再放回栈中，所以每加入一个运算符，相当于栈中数值的数量会减少1，这一点从上面的图中也能看出来，每

经过一个运算符，后面括号中的数值都比父节点小1。而每加入一个数值，后面括号中的数值都比父节点多1。

对上图的5种情况依次从左到右写成表达式：（数值用a表示，符号用+表示）

1. aaaa+++
2. aaa+a++
3. aaa++a+
4. aa+aa++
5. aa+a+a+

接下来我们只需要对4个数进行全排列，和对3个符号进行所有的组合，就可以无遗漏的计算所有可能情况。

四：后缀表达式方法的一些细节

采用后缀表达式方法，输出较容易。

采用后缀表达式需要实现4个数字的全排列，关于全排列又分为有序全排列和无序全排列，在我们这里两种方式都可以。

我的代码中对这两种方式都进行了实现。

其中， 字典序（有序）全排列思路参考： http://blog.csdn.net/visame/article/details/2455396

其实在STL的算法函数库中有字典序全排列的函数可以用，在“algorithm”文件里面定义了next_permutation函数和prev_permutation函数，

分别表示求有序全排列的下一个排列和上一个排列。其中的思路和所给链接中思路一样。

非有序全排列的方法也比较多，网上有很多介绍，我使用的是这篇文章介绍的一种很有趣的方法（进位不同数）

http://llfclz.itpub.net/post/1160/278490

有序全排列代码如下：

void SetNextSortPermutation(int *pIdx, int nLen)//调整到有序全排列的下一个排列
{
    int nCurIdx = nLen-1;
    int nFindIdx = nCurIdx;
    while (nCurIdx-1 >= 0 && pIdx[nCurIdx-1] > pIdx[nCurIdx])
    {
        nCurIdx--;
    }
    if (nCurIdx-1 < 0)
    {
        return;
    }
    while (pIdx[nFindIdx] < pIdx[nCurIdx-1])
    {
        nFindIdx--;
    }
    int tmp = pIdx[nCurIdx-1];
    pIdx[nCurIdx-1] = pIdx[nFindIdx];
    pIdx[nFindIdx] = tmp;
    for (int i = nCurIdx, j = nLen-1; i < j; i++, j--)
    {
        tmp = pIdx[i];
        pIdx[i] = pIdx[j];
        pIdx[j] = tmp;
    }
}

调整到运算符的下一个排列的算法类似四则运算中的进位处理，我们定义运算符的顺序是+-*/。则+++的下一个排列是++-，只需要将最后一个符号（+1）变成下一个符号，如果符号越界了，比如++/，最后一个符号是除法，加1，就需要回到加号，同时对前面的符号进行进位，在进位的过程中可能产生循环进位，所以要循环处理。

++/（加加除）的下一个排列是+-+，+//（加除除）的下一个排列是-++（减加加）。

对应的代码如下：

void SetNextOpComb(int *nOp, int nLen)//调整到运算符组合的下一个组合，类似运算中的进位处理
{
    int nCurIdx = nLen-1;
    while (nCurIdx >= 0 && 4 == ++nOp[nCurIdx])
    {
        nOp[nCurIdx] = 0;
        nCurIdx--;
    }
}

具体的模拟栈操作中，我定义了一个结点结构表示数值或者符号：

struct Node
{
    int nType;
    union
    {
        double d;
        int op;
    };
};

在实际的代码中使用list，只操作list的尾部来模拟栈。代码如下：

bool CalcStack(Node *node_all, int nLen)
{
    std::list<Node> lst;
    Node node;
    char output[200] = {0};
    char tmp[30] = {0};
    for (int i = 0; i < nLen; i++)
    {
        if (0 == node_all[i].nType)
        {
            lst.push_back(node_all[i]);
            sprintf_s(tmp, 30, "%2d ", (int)node_all[i].d);
            strcat_s(output, 200, tmp);
        }
        else if(1 == node_all[i].nType)
        {
            sprintf_s(tmp, 30, "%c ", g_op[node_all[i].op]);
            strcat_s(output, 200, tmp);
            Node f2 = lst.back();
            lst.pop_back();
            Node f1 = lst.back();
            lst.pop_back();
            if (abs(f2.d) < 0.0001 && 3 == node_all[i].op)
            {
                return false;
            }
            node.nType = 0;
            node.d = Operation(f1.d, f2.d, g_op[node_all[i].op]);
            lst.push_back(node);
        }
        else
            assert(0);
    }
    double f = lst.back().d;
    if (abs(f-24.0) < 0.0001)
    {
        g_Total++;
        printf("%s=%d\r\n", output, (int)f);
        return true;
    }
    return false;
}

五：后缀表达式方法的数值分析

后缀表达式方法共有5种合法的后缀表达式,假设abcd为4个数，+代表符号
第一种: abcd+++
第二种: abc+d++
第三种: ab+cd++
第四种: abc++d+
第五种: ab+c+d+
对于每种情况，4个数字的全排列=24，3个符号的可能性是4*4*4，所以每种情况有24*64=1536种
5种情况 共1536*5 = 7680 种排列

虽然从数据比较上来看，后缀表达式方式的情况比递归法的少，但由于我在代码中用到了list来模拟栈，所以实际代码运行的效率，递归法反而比后缀表达式方法更快，消耗的时间大约只有后缀表达式方法的1/10。也就是低一个数量级。

六：计算10以内（1到10）取4个数字用来算24点有多少种组合方式？

先明确一下题意，是组合而不是排列，所以1,2,3,4和2,1,3,4和4,3,2,1都是同一种组合。另外，可以取相同的数字，例如1,2,8,8、8,8,8,8，都是符合题意的。

这个问题，我们很容易写代码来计数，写一个4重循环如下：

    int nCount = 0;
    for (int a = 1; a <= 10; a++)
    {
        for (int b = a; b <= 10; b++)
        {
            for (int c = b; c <= 10; c++)
            {
                for (int d = c; d <= 10; d++)
                {
                    nCount++;
                }
            }
        }
    }

得到的计数值为 715。

那么这个数组我们怎样通过组合的知识算出来呢？

我们可以进行分类统计，4个数中：

没有相同的C(10，4) = 10!/(6!*4!) = 10*9*8*7/(4*3*2) = 5*3*2*7 = 10*21 = 210;
两两相同的C(10，2) = 45 取出2个数，剩下2个必须和取出2个一一对应
2个相同的 C(10，3) = 10*9*8/6 = 120 取出3个数，最后一个可能和取出的3个中任一个一样
3个相同的 C(10，2) = 10*9/2 = 45 取出2个数，其余2个可能和其中之一重复
4个相同的 C(10，1) = 10

所以得出一共有 C(10,4) + C(10,2) + C(10,3)*3 + C(10,2)*2 + C(10,1) = 715 种组合。

其中两两相同的那45个很容易漏计算。

但是这种计算方式是考虑4个数值的情况，如果我现在要取5个，6个数则不能推而广之，经过我在网上的搜素，得到如下公式：

M种数中取N个数的可重复组合（在概率论中叫做N次有放回无序抽样）记为：H(M,N) = C（M+N-1，N）。

也就是说：从M种数中取N个数的组合情况，和从M+N-1个数中取不重复的数的组合情况是一样的。

相关证明参考这篇文章，构造了两个一一对应的集合。http://wenku.baidu.com/view/e24419659b6648d7c1c74690.html

所以H(10，4) = C（13,4）= 13*12*11*10/24 = 13*11*5 = 143*5 = 715

和程序计算、分类统计的结果均一致。

在这715个组合中，共有566个组合是可以算出24点的，其余149个组合无法通过四则运算计算出24。

七：总结

虽然算24点是一个小程序，但是又涉及到了排列、组合的各种知识，还有像后缀表达式这样的一些应用，所以深究起来还是有很多可研究的东西。我在网上搜素了一些资料，比我的代码中考虑的更加周详。

http://blog.csdn.net/godmayknow/article/details/4249625 像这篇，里面提到了考虑到加法和乘法的交换律，所以在我们的表达式中还是有很多重复的表达式。

另外，在我的程序中一开始是使用float类型来计算小数的，但是最后发现计算所有10以内的组合的时候，比我从网上下载的一份所有组合要少一个能计算出来的表达式，经过比较分析，发现少了3,3,8,8,这一组合，本来8/(3-8/3) = 24，但是如果采用float类型计算8/(3-8/3)的值 = 24.000006。

而我检查的阙值又设置的很小0.000001。所以就漏掉了这一个可计算出24点的组合。我将float类型改成double类型，另外将阙值放的大一点，这一组就不会漏掉了。

递归法得到的一些结果：

 1  1  1  8  (( 1+ 1)+ 1)* 8 = 24
 1  1  2  6  (( 1+ 1)+ 2)* 6 = 24
 1  1  2  7  ( 1+ 7)*( 1+ 2) = 24
 1  1  2  8  (( 1* 1)+ 2)* 8 = 24
 1  1  2  9  ( 9- 1)*( 1+ 2) = 24
 1  1  2 10  (( 1+ 1)+10)* 2 = 24
 1  1  3  4  (( 1+ 1)* 3)* 4 = 24
 1  1  3  5  ( 1+ 5)*( 1+ 3) = 24
 1  1  3  6  (( 1+ 1)+ 6)* 3 = 24
 1  1  3  7  (( 1* 1)+ 7)* 3 = 24
 1  1  3  8  (( 1- 1)+ 3)* 8 = 24
 1  1  3  9  ( 3+ 9)*( 1+ 1) = 24
 1  1  3 10  (10-( 1+ 1))* 3 = 24
 1  1  4  4  (( 1+ 1)+ 4)* 4 = 24
 1  1  4  5  (( 1* 1)+ 5)* 4 = 24
 1  1  4  6  (( 1- 1)+ 4)* 6 = 24
 1  1  4  7  ( 7-( 1* 1))* 4 = 24
 1  1  4  8  ( 4+ 8)*( 1+ 1) = 24
 1  1  4  9  ( 1- 9)*( 1- 4) = 24
 1  1  4 10  (( 1+ 1)*10)+ 4 = 24

后缀表达式方法得到的一些结果：

 6  6  7 10 - * - =24
 6  8  6 - /  8 * =24
 6  6  8 -  9 * - =24
 6  6  8 + 10 - * =24
 6 10 +  6 /  9 * =24
 6  7  7 + 10 - * =24
 6  8  9  7 - / * =24
 6  7 *  8 10 + - =24
 6  7  9 -  9 * - =24
10  7 - 10 *  6 - =24
 8  6 -  8 *  8 + =24
 8  8 +  6 /  9 * =24
 6  8 10  8 - / * =24
 8  6  9  9 + / / =24
 6  8 10 -  9 * - =24
 9  6 / 10 *  9 + =24
10  6 10 10 + - - =24
 7  9  7 - * 10 + =24
 8  7  9 -  8 * - =24
 8 10 *  7  8 * - =24
 8  9 10  7 - / * =24
 7 10  8 - * 10 + =24
 8  8  8 10 - * - =24

最后感谢本文所引用以及未引用的相关资料的作者！

说明：本文相关源代码在下面网址可下载：

http://download.csdn.net/detail/sun2043430/5223200