霍夫变换检测直线

霍夫变换是一种全局检测直线的方法，速度慢，会将一些不连续的线段判定为连续的线段。

理论：

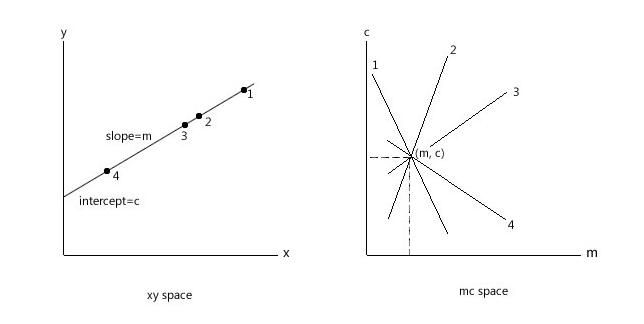
1.在图像中检测直线的问题，其实质是找到构成直线的所有的像素点。那么问题就是从找到直线，变成找到符合y=mx+c的所有(x,y)的点的问题。

2.进行坐标系变化y=mx+c，变成c=-xm+y。这样表示为过点（m,c）的直线束。

  

3.xy空间的直线上每一个点在MC坐标系中都表现为经过(m,c)的直线。找到所有点的问题，转变为寻找直线的问题。

4.对于图像中的每一个点，在MC坐标系中对应着很多的直线。找到直线的交点，就对应着找到图像中的直线。

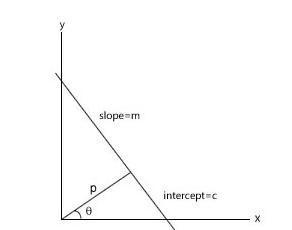
实际在使用这一原理的时候，不是采用直线的斜率和截距公式，而是用

如何实现：

1.       将θ角在-90度到90度的范围里，划分为很多区间，对所有的像素点(x,y)在所有θ角的时候，求出ρ.从而累加ρ值出现的次数。高于某个阈值的ρ就是一个直线。

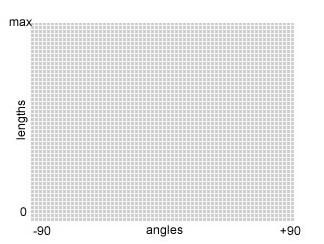
2.       这个过程就类似于如下一个二维的表格，横坐标就是θ角，ρ就是到直线的最短距离。

横坐标θ不断变换，对于所有的不为0的像素点，计算出ρ，找到ρ在坐标(θ,ρ)的位置累加1.

3.       上图中局部最大的就是找到的直线的θ和ρ的值。

代码简要说明：

    for( ang = 0, n = 0; n < numangle; ang += theta, n++ )
    {
        tabSin[n] = (float)(sin(ang) * irho);
        tabCos[n] = (float)(cos(ang) * irho);
    }

    // stage 1. fill accumulator
    for( i = 0; i < height; i++ )
        for( j = 0; j < width; j++ )
        {
            if( image[i * step + j] != 0 )
                for( n = 0; n < numangle; n++ )
                {
                    r = cvRound( j * tabCos[n] + i * tabSin[n] );
                    r += (numrho - 1) / 2;
                    accum[(n+1) * (numrho+2) + r+1]++;
                }
        }

    // stage 2. find local maximums
    for( r = 0; r < numrho; r++ )
        for( n = 0; n < numangle; n++ )
        {
            int base = (n+1) * (numrho+2) + r+1;
            if( accum[base] > threshold &&
                accum[base] > accum[base - 1] && accum[base] >= accum[base + 1] &&
                accum[base] > accum[base - numrho - 2] && accum[base] >= accum[base + numrho + 2] )
                sort_buf[total++] = base;
        }

    // stage 3. sort the detected lines by accumulator value
    icvHoughSortDescent32s( sort_buf, total, accum );

    // stage 4. store the first min(total,linesMax) lines to the output buffer
    linesMax = MIN(linesMax, total);
    scale = 1./(numrho+2);
    for( i = 0; i < linesMax; i++ )
    {
        CvLinePolar line;
        int idx = sort_buf[i];
        int n = cvFloor(idx*scale) - 1;
        int r = idx - (n+1)*(numrho+2) - 1;
        line.rho = (r - (numrho - 1)*0.5f) * rho;
        line.angle = n * theta;
        cvSeqPush( lines, &line );
    }

引用注明出处： http://www.cnblogs.com/smartvessel/archive/2011/10/20/2218654.html