OpenGL—坐标变换
OpenGL将3D物体渲染到2D平面,实质就是将一系列三维的顶点坐标变换到2D平面像素的一个过程,一般需要如下几种坐标变换方式:
坐标:
物体坐标:
物体自己绘制时的坐标,比如绘制一个三角形:
glBegin(GL_TRIANGLE_FAN); glVertex3f(1, 0, 0); glVertex3f(0, 1, 0); glVertex3f(0, 0, 1); glEnd();
设置的顶点坐标即为物体本身的坐标,即每个物体内部都有一个自己的坐标系,管理自己的位置。
全局坐标:
全局坐标 = 模型矩阵 * 三角形每个顶点坐标;全局坐标即物体相对整个空间的坐标。比如人这个实体,心脏是坐标中心,头就在心脏的上方,脚在心脏下方,这是相对物体的坐标来说的,也就是刚才的描述是在物体坐标下描述。而全局坐标即你这个人相对地球(假如整个地球就是我们要描述的空间)来说在哪个经纬度,这个就是全局坐标。
视觉坐标:
视觉坐标 = 模型视图矩阵 * 顶点坐标 = 视图矩阵 * 模型矩阵 * 顶点坐标;视觉坐标就是将当前全局的坐标转换到了相对眼睛看到的坐标。因为整个世界太大了,如果只想看某一部分,所以就引入了视觉坐标。视觉坐标就是定义了一个摄像机,看到场景中的哪些实体就将这些实体渲染出来,不在摄像机范围内的就不显示。视觉坐标就是将以摄像机的坐标为坐标原点,其他的物体都是相对摄像机的坐标来确定的。比如摄像机中的一个三角形,现在这个三角形在摄像机中的上面,还是下面,距离摄像机多远等,此时都是在视觉坐标下来计算的。
裁剪坐标:
裁剪坐标 = 投影矩阵 * 模型视图矩阵 * 顶点坐标;
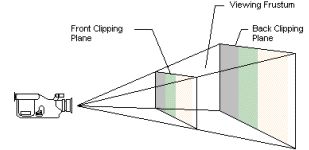
裁剪坐标就是经过投影矩阵裁剪后的坐标,比如上述定义的摄像机,这个摄像机看到的范围是有限的,有一个夹角和一个近距离和远距离。夹角外的看不到,设置一个近距离裁剪,就是太近的也当做看不见,太远的也看不见。也就是将上述的视觉坐标定义了一个裁剪体,在这个范围内的才渲染。同时将这个视觉坐标这些3d的顶点投影都这个视景体中,也就是差不多是最后2D的画面了。
标准设备坐标:
设备坐标 = 裁剪坐标 / w;此时设备坐标的x,y,z 范围是[-1, 1]之间
显示坐标:
即最后的显示在显示器上的坐标,也就是将[-1, 1] 与窗口的实际宽高对应。
矩阵:
模型矩阵:
全局坐标 = 模型矩阵 * 三角形每个顶点坐标;模型矩阵就是相对全局坐标的一种变换,比如在绘制物体之前,通过偏移,旋转,缩放等方式来对物体进行操作,那么物体的模型矩阵就是这些操作组成的矩阵。
glTranslated(); glRotated(); glScaled();如果自己实现则如下所示:
Matrix4 SceneObject::getTranslation()
{
Matrix4 mRet;
if (NULL != mParent)
{
mRet = mParent->getTranslation();
}
mRet *= mTranslate;
mRet *= mRotate;
mRet *= mScale;
return mRet;
} 这个返回的矩阵则为模型矩阵。其中mTranslate、mRotate和mScale分别是对矩阵进行的偏移、旋转和缩放等操作。
视图矩阵:
视觉坐标 = 模型视图矩阵 * 顶点坐标 = 视图矩阵 * 模型矩阵 * 顶点坐标;视图矩阵,也就是平时调用的gluLookAt所形成的矩阵,具体我们就来看下gluLookAt是形成如何的矩阵的。
void APIENTRY gluLookAt (
GLdouble eyex,
GLdouble eyey,
GLdouble eyez,
GLdouble centerx,
GLdouble centery,
GLdouble centerz,
GLdouble upx,
GLdouble upy,
GLdouble upz); gluLookAt有三类参数,第一类为眼睛的位置,即当前将摄像机的位置放置在哪个位置;第二类为观察点的位置,用于和眼睛的位置计算看的方向;第三类即摄像机朝上的位置,正常为y轴方向。
Matrix4 Camera::lookAt(Vector3 eyePos, Vector3 target, Vector3 up)
{
Vector3 zAxis = (target - eyePos).normalize();
Vector3 yAxis = up.normalize();
Vector3 xAxis = (zAxis.cross(yAxis)).normalize();
Matrix4 mat;
mat[0] = xAxis.x;
mat[1] = xAxis.y;
mat[2] = xAxis.z;
mat[4] = yAxis.x;
mat[5] = yAxis.y;
mat[6] = yAxis.z;
mat[8] = -zAxis.x;
mat[9] = -zAxis.y;
mat[10] = -zAxis.z;
Matrix4 pos;
pos.translate(-eyePos.x, -eyePos.y, -eyePos.z);
mat *= pos;
return mat;
} 如代码所示,首先计算摄像机的当前坐标,z轴为摄像机的朝向,y轴为摄像机的向上的方向,x轴通过z和y轴的叉乘所得。通过x,y,z轴组成摄像机的视图矩阵。最后将视图矩阵*世界坐标=视图坐标。也就是此时就是以摄像机当前的位置为原点,物体的位置都是相对摄像机的位置而言的。
投影矩阵:
裁剪坐标 = 投影矩阵*视图坐标;投影就是将3d世界中的物体投影到2d平面的一个过程,也就是我们看到的显示器上显示的东西。摄像机通过设置近裁剪平面和远裁剪平面和摄像机视角来形成一个视锥裁,通过这个视椎体来对场景中的物体进行裁剪,在视椎体之外的物体都不进行渲染,在视椎体内部的物体将通过投影的方式投影到2D的平面中。

正常的设置投影矩阵的opengl函数为glFrustum 或者 gluPerspective,通过设置视口的宽高,近裁剪与远裁剪等方式来形成一个投影矩阵,通过将投影矩阵与视图坐标相乘形成裁剪坐标。具体投影矩阵算法推倒可参照网上资料。
void Camera::setFrustum(float l, float r, float b, float t, float n, float f)
{
mMatrixProjection.identity();
mMatrixProjection[0] = 2 * n / (r - l);
mMatrixProjection[2] = (r + l) / (r - l);
mMatrixProjection[5] = 2 * n / (t - b);
mMatrixProjection[6] = (t + b) / (t - b);
mMatrixProjection[10] = -(f + n) / (f - n);
mMatrixProjection[11] = -(2 * f * n) / (f - n);
mMatrixProjection[14] = -1;
mMatrixProjection[15] = 0;
}