简单处理海量数据:STL的hasp_map使用+堆排序
一:简介
我觉得数据结构与算法的应用最重要地就是考虑如何更效率地处理数据,而其中很重要的一方面,就是处理海量数据。本次课程设计的假设背景:今天百度通过日志文件把用户每次检索使用的所有检索串都记录下来,每个查询串的长度为1-255字节,假设目前有一千万个记录,即1000万次查询(这些查询串的重复度比较高,虽然总数是1千万,但如果除去重复后,不超过3百万个。一个查询串的重复度越高,说明查询它的用户越多,也就是越热门。),从中统计最热门的10个查询串,要求使用的内存不能超过1G。
这是一个面试题,网上有一些解决思路,但没有实现代码,甚至没伪代码,根据网友提供的思路,我试试能否表达出来。
(在这里我们得做一份数据,含300万个不同的搜索词,从TOP1至TOP10的搜索次数分别是100万、90万、80万…10万,其它搜索词搜索量均在10万以下。开始做数据的时候,本来是想#include<vector>//动态数组#include <algorithm> //容器算法,用来随机输出数据,但最后放弃这个思路了,因为比较复杂,时间又不多。就直接随机输出1000万个0~300万的随机数。)
(在这里我们得做一份数据,含300万个不同的搜索词,从TOP1至TOP10的搜索次数分别是100万、90万、80万…10万,其它搜索词搜索量均在10万以下。开始做数据的时候,本来是想#include<vector>//动态数组#include <algorithm> //容器算法,用来随机输出数据,但最后放弃这个思路了,因为比较复杂,时间又不多。就直接随机输出1000万个0~300万的随机数。)
所以本课程设计:有1000万个0~300万的随机数
,
找出出现次数前10的数字。
二: 算法说明(来自 http://blog.csdn.net/v_JULY_v/article/details/6256463 )
大概有300万个不同的数据,对这300万个数据进行排序,得出TOP10数据。
1.hash统计:先对这批海量数据预处理。具体方法是:维护一个Key为Query字串,Value为该Query出现次数的HashTable,即hash_map(Query,Value),每次读取一个Query,如果该字串不在Table中,那么加入该字串,并且将Value值设为1;如果该字串在Table中,那么将该字串的计数加一即可。最终我们在O(N)的时间复杂度内用Hash表完成了统计;
2.堆排序:第二步、借助堆这个数据结构,找出Top K,时间复杂度为N‘logK。即借助堆结构,我们可以在log量级的时间内查找和调整/移动。因此,维护一个K(该题目中是10)大小的小根堆,然后遍历大约300万的Query,分别和根元素进行对比。
3.最终的时间复杂度是:O(N) + N' * O(logK),(N为1000万,N’为300万)。
三:实验步骤
1:制作数据源(data.txt),大小76.2 MB,制作时间114.984秒。制作环境:CPU:[email protected] 内存:2GB
主要代码如下:
……
for(int i=0;i<10000000;i++)
{
int a = (rand()%30000)*(rand()%100);//产生范围是0~300万
ofile<<a<<endl;
}
2:载入数据,存到std::hash_map容器,存下各个“搜索词”的“搜索量”。
首先介绍下hash_map容器,有点像一个数组,只不过它的“下标”不是数字,可以是string等类型,它是一种“关键码Key-属性Value”对的集合。
这里时间有限,直接使用std来应用,不然还要写哈希表,更进一步的话就还要了解除法、平方或斐波那契散列发。
根据网上的文章,对于大量的数据,比较适合使用hash_set。
主要是打开数据文件data.txt,然后加上代码:
while(ifile.good())
{
ifile>>m_query;
Query[m_query]+=1; //使用std的hash_map容器(基于搜索树?)//此处是重载,会自动判断,选择插入或更新。
//总代码请看源程序
}
while(ifile.good())
{
ifile>>m_query;
Query[m_query]+=1; //使用std的hash_map容器(基于搜索树?)//此处是重载,会自动判断,选择插入或更新。
//总代码请看源程序
}
3: 排序得出TOP10结果
因为这里只需要得出TOP10数据,所以只需要设计一个结构存储初始的10个数据,再通过遍历比较来更新结构里的10个数据。 若对比的数据量比较少的话,使用普通的数组来接收并且比较数据即可。
本课程设计将使用堆排序进行统计。
根据需求,本课程的堆算法需要维护一个大小为10的最小堆,然后遍历300万的Query,分别和根元素(堆顶)进行对比。
首先要认识堆:其实就是一个近似完全二叉树的结构。以最小堆为例(最大堆就反之),它的父节点总是<=任何一个子节点的键值。
(现在突然遇到一个问题:遍历hash_map容器的时候,如何根据指针来获取hasp_map的key值?后面用一整个上午才把它理清楚了一点。先搁着,先介绍下堆算法先。http://blog.csdn.net/vozon/article/details/5458370)
构造一个最小堆后,根元素(最顶层)是TOP10中最小的,从数据源取出一个数据来和根元素比较,若比根元素还小,那就不用管它,继续取下一个数据。若比根元素大,那就要删了根元素,然后调整重建堆(从上往下FixDown),再在最后位置插入新的数据,然后调整重建堆(从下往上FixUp)。这是由堆的性质来决定。参考资料: http://blog.csdn.net/morewindows/article/details/6709644
根据参考资料,我写了一个最小堆的类MinHeap,包含初始化堆话数组、插入、删除、排序等功能。
4:整合
如果单单使用hash_map<string,int> Query;好像只能进行存储而不能进行操作。一开始查找了很多文章,查找相关成员函数,最后发现还有一个神奇的东西 iterator(迭代器)。定义方法 hash_map<string,int>::iterator itr;简单来说,就可以遍历了。方法:for(itr=Query.begin();itr!=Query.end();itr++){}
但是要怎样与堆排序结合起来?我写的堆,接收的是一个int数组,而本设计的hasp_map是string “下标"。 还有一个问题,iterator是什么类型?它好像是不能保存的或者说最好不要保存它,因为它会随着数据量的改变而改变。最后决定,创建一个string数组来接收当前top10的key值。开始动手的时候,发现了一个严峻的问题,我为什么是写成最小堆了?我需要的是最大堆呀。又想想,好像也可以。堆顶是Top10中最小的,新来的数据与它比较,比它小的话就跳过,比它大的话就删了堆顶,插入新的数据。这时发现,用string数组来接收当前top10的key值不合算。还是使用一个结构体struct KeyValue//储存Query信息{string key; int value;};
而且,遍历完一次数据后,把“搜索”TOP10的数据的value值保存在heap数组了,还要再遍历一次,根据value值查找对应的key值,保存在KeyValue m_KeyValue[10]中。
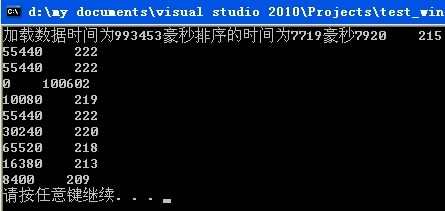
最后是一两个小时的痛苦的调试时间,下图是第一个有点样子的结果。
四:实验总结
本次课程设计并没有解决快速处理数据的问题。刚开始加载数据是200多秒,后来不知道为什么变成了900多秒。其实,加载数据这部分,自己感觉多于50秒就让这次设计没什么“用”了,辛辛苦苦做的结构与算法,排序用了7719毫秒,也就是7秒多,但整个程序确花费了将近17分钟。最后的排序也还不完善,并没有从大到小显示,但期末实在是时间问题。制作的数据包因为都是时间随机数,所以结果列表有点单调。 有空要去研究下怎样快速加载数据,估计要使用数据库或者什么分而治之、多线程……本设计也没有对比堆排序和其它排序的效率问题。
收获:1.亲手写了一遍堆结构与算法,现基本认识了堆排序。
2.使用STL的<hasp_map>,掌握了容器的基本用法。
3.阅览了挺多的资料,提高了对数据结构、算法与数学的认识。
//----------------------------后话------------------------
看书的时候,突然发现,有一种文件映射的通信方式,它可以让程序快速读取文件。找个时间学习一下,并且把它给实现了,顺便接触下操纵系统。
//----------------------------------------------------------
最后是代码:
一:堆
#include <iostream>
using namespace std;
class MinHeap
{
public:
//构造函数
MinHeap();//默认构造一个heap[10]大小的堆
MinHeap(int arr[],int n);//接收一个外部数组,自定义大小
~MinHeap();//析构
//数组赋值
void SetArrayVaual();
////堆话数组(最小堆)//放到构造函数实现
//bool MakeMinHeap(int a[],int n);
//将x插入最小堆的最底部
bool Insert(const int &x);
//删除堆顶(最小元素)
bool RemoveMin();
//获取堆顶数值
int GetMinheap();
//判断空否
bool IsEmpty()const;
//判断满否
bool IsFull()const;
//置空堆
void MakeEmpty();
//堆排序
int * MinHeapSort();
private:
int *heap;
int currentSize; //最小堆中当前元素个数
int maxHeapSize; //最小堆最多允许的个数
void siftDown(int start,int m);//从start到m下滑调整成为最小堆
void siftUp(int start);//从start到0上滑调整成为最小堆
};
//---------------构造函数------
MinHeap::MinHeap()//默认构造一个heap[10]大小的堆
{
maxHeapSize=10;
heap=new int[maxHeapSize];//创建堆存储空间
currentSize=0;//建立当前堆大小
}
MinHeap::MinHeap(int arr[],int n)//接收一个外部数组,自定义大小
{
maxHeapSize=(n>10)?n:10;
heap=new int[maxHeapSize];
for(int i=0;i<n;i++)//接收数组
{
heap[i]=arr[i];
}
currentSize=n;//当前堆大小
int currentPos=(currentSize-2)/2;//*******找最初调整位置:最后带分支的节点位置*********
while(currentPos>=0)//自底向上逐步扩大成为堆
{
siftDown(currentPos,currentSize-1);//局部自上向下 下滑调整
currentPos--;//再向前换一个分支节点
}
}
//------析构函数--------
MinHeap::~MinHeap()
{
delete []heap;
}
//---------从start到0上滑调整成为最小堆------
//如果被修改的对象在底部,就siftUp
void MinHeap::siftUp(int start)
{
int j=start;//子节点
int i=(j-1)/2;//父节点
int temp=heap[j];//保存start点的值
while(j>0)//父节点存在时
{
if(heap[i]<=temp)//当父节点值小,不调整。
break;
else//当父节点值大,调整
{
heap[j]=heap[i];//子节点值等于父节点值
j=i;//子节点上移
i=(i-1)/2;//父节点上移
}
//回送
heap[j]=temp;
//若不需调整,此代码不影响任何结果
//若需要调整,值大的父节点的值会成为子节点的值,最后父节点的值是(它到底部)中最小的。
//上滑,就是将开始点的值上移,直到它碰到父节点比它小。而不是一直判断到顶部使整条链有序。
}
}
//-------------从start到m下滑调整成为最小堆---------------
//如果被修改的对象在顶部,就siftDown
void MinHeap::siftDown(int start,int m)
{
//如果子女的值小于父节点的值,自上向下调整。关键码小的上浮,形成局部的最小堆
int i=start;//父节点
int j=2*i+1;//左子节点
int temp=heap[i];//保留开始值
while(j<=m)
{
if(j<m&&heap[j]>heap[j+1])//如果左子节点比右子节点大,要让右子节点上浮
j++;
if(temp<=heap[j])//从start点到j点,已经符合最小堆情况了
break;
else
{
heap[i]=heap[j];
i=j;
j=2*j+1;
}
heap[i]=temp;//回放temp中暂存的元素
}
}
//---------将x插入最小堆的最底部,然后向上调整----------
bool MinHeap::Insert(const int &x)
{
if(currentSize>=maxHeapSize)
{
//cerr<<"Heap Full"<<endl;
return false;
}
heap[currentSize]=x;//插入
siftUp(currentSize);//向上调整
currentSize++;//堆个数加1
return true;
}
//----------删除堆顶(最小元素)---------------
bool MinHeap::RemoveMin(/*int &x*/)
{
if(!currentSize)//若currentSize==0
{
// cerr<<"Heap Empty"<<endl;
return false;
}
//x=heap[0];//????????为什么要传给值进来接收堆顶元素??????
heap[0]=heap[currentSize-1];//最后元素填补到根节点
currentSize--;
siftDown(0,currentSize-1);
return true;
}
//-----------获取堆顶数值---------
int MinHeap::GetMinheap()
{
return heap[0];
}
//-----------------排序得到从大到小排列的数组----------------
//此处很多不完善的地方。完全破坏最小堆等。应该用要返回一个数组,以“删除堆顶”的形式获取最小值赋值给另一个数组。
//后来想清楚了,删除或者siftDown等函数都是操纵*heap,所以肯定会破坏。
int * MinHeap::MinHeapSort()
{
int *arr=new int[maxHeapSize];
//arr=heap;
////cout<<endl<<heap[0]<<heap[1]<<heap[9]<<endl;
////cout<<endl<<arr[0]<<arr[1]<<arr[9]<<endl;
//int temp;
//for(int i=currentSize-1;i>=1;i--)
//{
// //交换值
// temp=arr[0];
// arr[i]=arr[0];
// arr[0]=temp;
// //交换后,arr[i]就是0~i最小的。
// siftDown(0,i);//堆顶值换了,0~i-1重新调为最小堆(教程里是0~i????)
//}
for(int i=0;i<10;i++)
{
arr[9-i]=heap[i];
RemoveMin();
}
return arr;
}
二:主区域代码:
#include <iostream>
#include<fstream>
#include<ctime>
#include<string>
#include<hash_map>
#include"MinHeap.h"//最小堆
using namespace std;
int main()
{
clock_t t_begin,t_end;
string m_query;//查询的字符串(本程序用数字字符串来表示不同的搜索词)
ifstream ifile;//载入数据
hash_map<string,int> Query;//储存数据的映射结构体,自动计数
hash_map<string,int>::iterator itr;//!!!hasp_map的迭代器,用于操作。
MinHeap m_MinHeap;//堆排序对象。默认构造一个heap[10]大小的堆
//-------------加载数据,载入到hasp_map结构---------
ifile.open( "data.txt", ios::in );
if( !ifile )
{
cerr << "文件不能打开" << endl;
return 0;
}
t_begin=clock();
while(ifile.good())
{
ifile>>m_query;
Query[m_query]+=1;//此处是重载了,会自动判断,选择插入或更新。
}
t_end=clock();
cout<<"加载数据时间为"<<t_end-t_begin<<"豪秒";
//-------------------------------
//------------排序-------------
t_begin=clock();
struct KeyValue//储存Query信息
{
string key;
int value;
};
KeyValue m_KeyValue[10];
int i=0;
//做一个原始堆
for(itr=Query.begin();itr!=Query.end();itr++)
{
if(i>=10)
break;
m_MinHeap.Insert(itr->second);
i++;
}
//比较value排序
for(itr=Query.begin();itr!=Query.end();itr++)
{
if(itr->second>m_MinHeap.GetMinheap())
//堆顶是Top10中最小的,新来的数据与它比较,比它小的话就跳过,比它大的话就删了堆顶,插入新的数据。
{
m_MinHeap.RemoveMin();
m_MinHeap.Insert(itr->second);
}
}
int *arr;
arr=m_MinHeap.MinHeapSort();
//再遍历获取key
for(itr=Query.begin();itr!=Query.end();itr++)
{
i=0;
if(i>=10)
break;
for(int j=0;j<10;j++)
{
if(itr->second==arr[j])
{
m_KeyValue[j].key=itr->first;
m_KeyValue[j].value=itr->second;
}
}
i++;
}
t_end=clock();
cout<<"排序的时间为"<<t_end-t_begin<<"豪秒";
for(int j=0;j<10;j++)
{
cout<<m_KeyValue[j].key<<" "<<m_KeyValue[j].value<<endl;
}
system("PAUSE");
return 0;
}