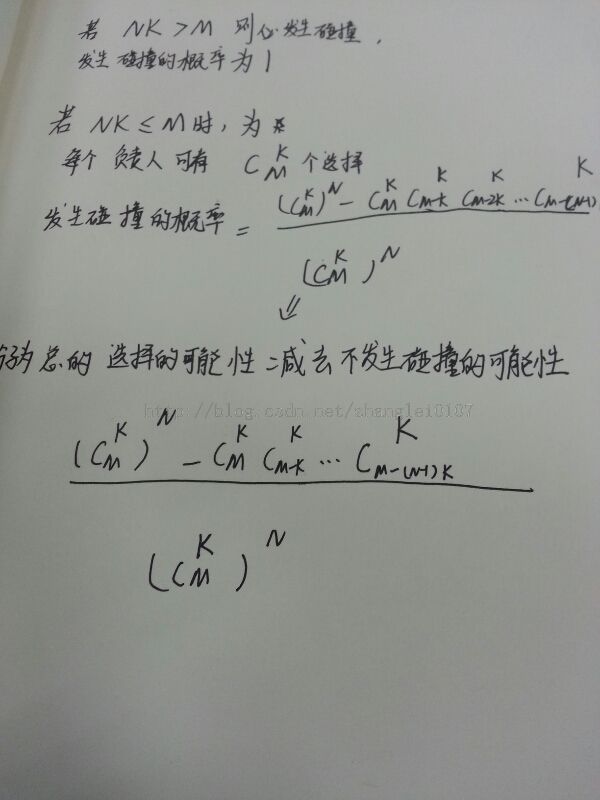某公司笔试题
14:如下函数,在32bit系统foo(2^31-3)的值是:
Int foo(int x)
{
return x&-x;
}
A: 0 B: 1 C:2 D:4
2与31异或,10与11111异或后得11101,3为11,11101-11=11010
-11010相当于11010取反加1为00110
11010&00110=10,结果为2
宿舍内5个同学一起玩对战游戏,每场比赛有一些人作为红方,一些人作为蓝方。请问至少需要多少场比赛,才能使任意两个人之间有一场红方对蓝方和蓝方对红方的
比赛。
分析:一次划分中,某方可以有1人,另一方有4人或某方有2人,另一人有3人。
要使任意两个人之间有一场红方对蓝方和蓝方对红方的比赛,假设5个同学为A,B,C,D,E,相当有有向图的5个节点,任意两个节点间有两个方向的边连接。
即总的节点关系有(5个节点中选取两个节点)A(5,2)=5*4=20个关系。
而一次比赛(一次划分)能够生成的关系(一方两人一方三人的划分)c(2,1)*c(3,1)=2*3=6或者(一方四人一方一人的划分)c(4,1)*(c(1,1)=4*1=4,
所以一场比赛(一次划分)最多生成的关系次数为6
所以需要20/6=3.33..即至少需要4场比赛
用两种颜色去染排成一个圈的6个棋子,如果通过旋转得到则只算一种,一共有多少种染色
答案共14种
分析:题目意思是说旋转后相同的颜色排布算一种。相当于棋子没有区别,只有位置的相对关系。
设两种颜色为黑白
全黑1种+全白1种=2
1黑5白(1种)+1白5黑(1种)=2种
2黑4白(2个黑的可以紧挨着,2个黑的中间隔1个棋子,两个黑的中间隔2个棋子)共3种
4黑2白同2黑4白对称:3种
3黑3白:3个黑的连在一起(1种),3个黑的任意两个之间不相邻(1种),3个黑的有两个挨着,另外一个与这两个棋子都不相邻(2种)
共4种
特别是另外一个与这两个棋子都不相邻的情况,有两种,刚开始以为是对称的算一种了,而实际上是两种,因为这种通过旋转是转不到一样的。
所以总共有2+2+3+3+4=14种
To speed up data access , we build cache system. In one system , The L1 cache access time is 5 ns , the L2 cache access time is 50 ns and the memory access time is 400 ns. The L1 cache miss rate is 50% , the L2 cache miss rate is 10%. The average data access time of this system is:(5 Points)
Average Memory Access Time = Hit time + Miss rate × Miss Penalty
Average Memory Access Time =
L1 Hit time + L1 Miss rate * L1 Miss penalty
L1 Miss penalty =
L2 Hit time + L2 Miss rate * L2 Miss penalty
5+0.5*(50+0.1*400)=50ns
定义一个二进制数字串的“长度”为从最右侧开始算起连续1的个数(说明,如果最右侧为0,则长度为0,如果最右侧为1,则开始数连续的1的个数作为长度)。例如length(100011)=2,length(100000)=0,请分析一个随机的N位字串的“长度”的期望值是多少
注意这个长度是从最右侧算起的,比如length(111011)=2,即使,字符串左边出现更长的长度
某公司的销售专家需要拜访商家,假设本市总共有M家商家,某公司派了N位销售专家来拜访本市的商家。假设专家之间互不通信,每位专家随机选择K个商家。如果有多位专家拜访了一个商家,我们称之为拜访碰撞。问发生拜访碰撞的概率是多少?
有3种规格的糖果,分别为每包6颗,每包9颗,每包140颗,如果需要8颗的话,就要对糖果进行拆包。当所需的糖果数字N>=某个数量时
,糖果便不需要进行拆包,问N的值为多少
分析6=3*2,9=3*3,6和9均为3的倍数,而任意因子个2和3的组合可以组成2,3,4,5,6,7..(即>=2的任意整数),所以
6和9的组合可以表示>=6的3的倍数。而140%3=2(取模运算).。所以140+6=146可以用6,9,140的组合表示。
即可以表示>=146(即140+3*n,n>=2)对3求模余2的所有的数,所有数对3求模要么余0(已经可以表示3的倍数),要么余1,要么余2(余2的>=146的数已经可以表示)
要对3求模余1可以使140翻倍至280。280对3求模便余1,说明140的2倍已经可以表示对3求模余1的数。那么280+3*n的组合(3n>=6)便可以表示
(即>=286的数),这样所有的数已经可以表示。是不是答案就是286呢,答曰不是的。
因为285可以被3整除,284对3求模余2且>146,所有284便是答案
此题的解法用了取模的思想。所有的整数数对某个数k取模要么为0,1,2,3,...k-1。只要能覆盖着k种情况,便可以表示所有的整数