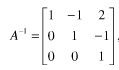〖数学算法〗逆矩阵算法
矩阵大家一定都很熟悉,它是线性代数中的一个术语,它在生产实践,科研,等各学科都有不可替代的作用,求逆矩阵当然是矩阵的一种常用操作,今天就写了个求逆矩阵的程序巩固下基本功。
首先让我们回忆一下你矩阵的定义:
逆矩阵:设A是数域上的一个n阶方阵,若在相同数域上存在另一个n阶矩阵B,使得: AB=BA=E。 则我们称B是A的逆矩阵,而A则被称为可逆矩阵。
接下来我带大家回忆一下在“线性代数”中求逆矩阵的两种方法:
(以下方法来至维基百科)
1.伴随矩阵法
如果矩阵可逆,则其中是的伴随矩阵。
注意:中元素的排列特点是的第列元素是的第行元素的代数余子式。要求得即为求解的余因子矩阵的转置矩阵。
2. 初等变换法
由条件以及矩阵乘法的定义可知,矩阵和都是方阵。再由条件以及定理“两个矩阵的乘积的行列式等于这两个矩阵的行列式的乘积”可知,这两个矩阵的行列式都不为0。也就是说,这两个矩阵的秩等于它们的级数(或称为阶,也就是说,A与B都是方阵,且rank(A) = rank(B) = n)。换句话说,这两个矩阵可以只经由初等行变换,或者只经由初等列变换,变为单位矩阵。
因为对矩阵施以初等行变换(初等列变换)就相当于在的左边(右边)乘以相应的初等矩阵,所以我们可以同时对和施以相同的初等行变换(初等列变换)。这样,当矩阵被变为时,就被变为的逆阵。
接下来让我们来分别看看两个实际的小题,回忆一下解法:
1.伴随矩阵法求逆矩阵:
问题:
求解过程:
2.初等变换法:
问题:
求解过程:
解得:
接下来我就用第二种方法,做一下第一题,代码如下:
public class NiMatrix {
private double[][] getNiMatrix(double[][] matrix) {//求逆矩阵函数
/*定义扩展矩阵*/
double[][] expand_matrix = new double[matrix.length][matrix.length * 2];
/*定义得到的逆矩阵*/
double[][] new_matrix = new double[matrix.length][matrix.length];
/*初始化扩展矩阵*/
initExpandMatrix(matrix,expand_matrix);
/*调整扩展矩阵,若某一列全为0,则行列式的值等于0,不存在逆矩阵*/
boolean canAdjust = adjustMatrix(expand_matrix);
if(false == canAdjust)//如果不存在逆矩阵,返回NULL
return null;
/*计算扩展矩阵*/
calculateExpandMatrix(expand_matrix);
/*用计算过的扩展矩阵取后面的N*N矩阵,为所求*/
getNewMatrix(expand_matrix,new_matrix);
return new_matrix;
}
/*初始化扩展矩阵*/
private void initExpandMatrix(double[][] init_matrix,double[][] expand_matrix) {
for (int i = 0; i < expand_matrix.length; i++)
for (int j = 0; j < expand_matrix[i].length; j++) {
if (j < expand_matrix.length) {//左边的N*N矩阵原样赋值
expand_matrix[i][j] = init_matrix[i][j];
} else { //右边N*N赋值为单位矩阵
if (j == expand_matrix.length + i)//如果为右边矩阵的对角线就赋值为1
expand_matrix[i][j] = 1;
else
expand_matrix[i][j] = 0;
}
}
}
/*调整扩展矩阵,若某一列全为0,则行列式的值等于0,不存在逆矩阵*/
private boolean adjustMatrix(double[][] expand_matrix) {
for (int i = 0; i < expand_matrix.length; i++) {
if (expand_matrix[i][i] == 0) {//如果某行对角线数值为0
int j;
/*搜索该列其他不为0的行,如果都为0,则返回false*/
for (j = 0; j < expand_matrix.length; j++) {
if (expand_matrix[j][i] != 0) {//如果有不为0的行,交换这两行
double[] temp = expand_matrix[i];
expand_matrix[i] = expand_matrix[j];
expand_matrix[j] = temp;
break;
}
}
if (j >= expand_matrix.length) {//没有不为0的行
System.out.println("此矩阵没有逆矩阵");
return false;
}
}
}
return true;
}
/*计算扩展矩阵*/
private void calculateExpandMatrix(double[][] expand_matrix) {
for (int i = 0; i < expand_matrix.length; i++) {
double first_element = expand_matrix[i][i];
for (int j = 0; j < expand_matrix[i].length; j++)
expand_matrix[i][j] /= first_element;//将该行所有元素除以首元素
/*把其他行再该列的数值都化为0*/
for (int m = 0; m < expand_matrix.length; m++) {
if (m == i)//遇到自己的行跳过
continue;
double beishu = expand_matrix[m][i];
for (int n = 0; n < expand_matrix[i].length; n++) {
expand_matrix[m][n] -= expand_matrix[i][n] * beishu;
}
}
}
}
/*用计算过的扩展矩阵取后面的N*N矩阵,为所求*/
private void getNewMatrix(double[][] expand_matrix, double[][] new_matrix) {
for(int i = 0; i < expand_matrix.length; i++)
for(int j = 0; j < expand_matrix[i].length; j++){
if(j >= expand_matrix.length)
new_matrix[i][j-expand_matrix.length] = expand_matrix[i][j];
}
}
/*打印矩阵*/
public void printMatrix(double[][] matrix){
for (double[] tempi : matrix) {
for (double tempj : tempi) {
System.out.print(tempj + " ");
}
System.out.println();
}
}
/*矩阵做乘法,验证结果*/
private static double[][] getProductMatrix(double[][] init_matrix,
double[][] new_matrix) {
int len = init_matrix.length;
double[][] product_matrix = new double[len][len];
for(int i = 0; i < len; i++){
for(int j = 0; j < len; j++)
for(int k = 0; k < len; k++)
product_matrix[i][j] += init_matrix[i][k] * new_matrix[k][j];
}
return product_matrix;
}
public static void main(String[] args) {
NiMatrix _robot = new NiMatrix();
System.out.println("=====原矩阵=====");
double init_matrix[][] = {
{ 1, 2, -1 },
{ 3, 4, -2 },
{ 5, -4, 1 }
};
_robot.printMatrix(init_matrix);
System.out.println("=====逆矩阵=====");
double new_matrix[][] = _robot.getNiMatrix(init_matrix);
_robot.printMatrix(new_matrix);
System.out.println("=====原矩阵*逆矩阵=====");
double[][] product_matrix = getProductMatrix(init_matrix,new_matrix);
_robot.printMatrix(product_matrix);
}
}
测试结果:
==================================================================================================
作者:nash_ 欢迎转载,与人分享是进步的源泉!
转载请保留原文地址:http://blog.csdn.net/nash_/article/details/8241348
===================================================================================================