Comprehensions on Group NMF

最近看了一下group sparsity和group structure方面的东西，本文主要针对了其中一种在NMF上的应用得到的group sparsity总结了一些东西。这篇理论上的文章没有被引用很多，但是其在EEG上用Group NMF做得一篇文章倒是有些影响力的。具体参考reference吧。总的来说，group sparsity或者单纯的sparsity对于一些有物理意义的东西比较好解释，我们通常觉得一些东西的基（basis，or say, feature）和令一些东西的基是不同的，所以可以按照sample分group，或者feature分group。现在group的东西也做得差不多了，从当初的group Lasso到group PCA，再到本文中的Group NMF。但不知道引用率少是关注的人少呢还是效果不好呢？！不忍吐槽下现在拼性能的坑爹研究环境，如果应用一个东西效果不好都没人发paper了……不说废话，看Group NMF！

Comprehensions on Group NMF

Rachel Zhang

 

1.      Brief Introduction

1.      Whyuse Group Sparsity?

An observation that features or data items withina group are expected to share the same sparsity pattern in their latent factorrepresentation.

假设的Group sparsity就是从属于同一个group的数据项或者特征在low-rank 表示中有相似的sparsity pattern.

2.      Differencefrom NMF.

As a variation of traditional NMF, Group NMF considersgroup sparsity regularization methods forNMF.

3.      Application.

Dimension reduction, Noise removal in text mining,bioinformations, blind source separation, computer vision. Group NMFenable natural interpretation of discovered latent factors.

4.      What is group?

Different types of features, such as in CV: pixelvalues, gradient features, 3D pose features, etc. 同种feature组成一个group

 

 

 

 

 

2.      Relatedwork

5.      Relatedwork on Group Sparsity

5.1.      Lasso(The Least Absolute Shrinkage and Selection Operator)

l₁-norm penalized linear regression

(1)

5.2.      GroupLasso

Group sparsity using l_1,2-norm regularization

(2)

where the sqrt(p_l)terms accounts for the varying group sizes

5.3.      Sparsegroup lasso

(3)

5.4.      Hierarchicalregularization with tree structure，2010

          R. Jenatton, J. Mairal, G. Obozinski, and F. Bach. “Proximal methods forsparse hierarchical dictionary learning”. ICML 2010

5.5.      Thereare some other works focus on group sparsity on PCA

6.      Relatedworks on NMF

6.1      AffineNMF: extending NMF with an offset vector. Affine NMF is used to simultaneouslyfactorize.

 

 

 

 

 

3.       Problem to Solve

Consider a matrix X∈ R^m×n .Assume that the rows of Xrepresent features and the columns of Xrepresent data items.

7.       In standard NMF, we are interested in discovering two low-rankfactor matrices W and H by minimizing an objective function:

constrain W>=0 and H>=0

8.       Group structure and Group sparsity

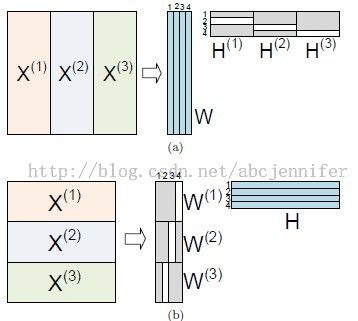
In this figure, (a)中group分sample， 对于basis W, 一个group内系数H的sparsity相同; (b)中group分feature，group sparsity体现在latent component matrices的构造中。

9.       In group NMF, objective function:

That is, the l1,q-norm of a matrix is the sum ofvector l_q-norms of its rows.

所以，||Y||_1,q 的惩罚项希望得到Y中的0行越多越好。

在这里，b个类，每一类的X^(b)和H^(b)不同，所以obj function希望使得H^(b)中有尽可能多的0行, 刚好符合我们的group sparsity。

 

 

 

 

 

4.       Optimization Algorithms

With mixed-norm regularization, the minimization problembecomes more difficult than the standard NMF problem. We here propose twostrategies based on the block coordinate descent (BCD) method in non-linearoptimization. In both algorithms, the l_1,q-normterm is handled via Fenchel duality.

10.   Thefirst method – Matrix-block BCD method for (5)

           In this method, a matrix variable is minimized ateach step fixing all other entries.

(4.3) is solved by nonnegativity-constrainedleast squares (NNLL)

Now considerthe problem in (4.4), it can be rewritten by

其中第一项可微，导数连续，第二项convex。那么可用一个凸优化解决。

Algo 2 是(4.7)的一种解决方法（variant of Nesterov’s first order method），其中主要需要解决的是(4.6) 按行更新，可以看做解决：

而这个非负约束可以由(4.9)消除掉（其解为(4.8)的全局最优解）

其证明见Reference [1]. 而(4.9)就可以由(4.11) 解决了：

where ||·||_q* isthe dual norm of ||·||_q.

q=2时，||·||_q*=||·||₂

q=∞时，||·||_q*=||·||₁

 

 

11.   The secondmethod is a BCD method with vector blocks; that is, avector variable is minimized at each step fixing all other entries.

          Recent observations indicate that the vector-block BCD method is also very efficient, oftenoutperforming the matrix-block BCD method. Accordingly, we develop thevector-block BCD method for (5) as follows.

           In the vector-block BCD method, optimal solutions tosubproblems with respect to each column of W andeach rows of H(1), ··· ,H(b) are sought.

The solution of (4.14) is given as a closed form:

Subproblem (4.15) is easily seen to be equivalent to

Which is a special case of (4.8)

 

12.   Remark on the two optimizing methods:

Optimization Variables in (5): {W, H⁽¹⁾,…,H^(B)}

Matrix – BlockBCD method: divides the variables into (B+1) blocks: W, H⁽¹⁾,…, H^(B)

Vector –Block BCD method: divides the variables into k(B+1) blocks, represented by thecolumns of W, H⁽¹⁾,…, H^(B)

Both methodseventually rely on dual problem (4.11).

  

 

 

5.       Result:

6.      Reference

1.      JinguKim et al. “Group Sparsity in Nonnegative Matrix Factorization”

2.      NMF代码http://www.csie.ntu.edu.tw/~cjlin/nmf/

3.      “Algorithmsfor NMF” http://hebb.mit.edu/people/seung/papers/nmfconverge.pdf

4.      NMFtoolbox http://cogsys.imm.dtu.dk/toolbox/nmf/

5.       "Group Nonnegative Matrix Factorization for EEG Classification"