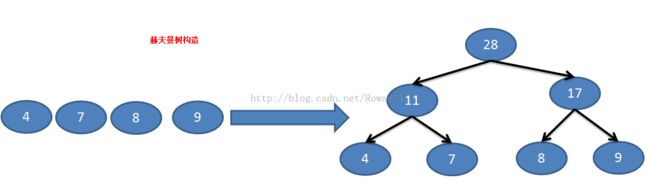
由二叉树构造赫夫曼树

赫夫曼树：

假设有n个权值{w1,w2,w3....},试构造一棵具有 n个叶子节点的二叉树，每个叶子节点带权为wi，则其中 带权路径长度最小的二叉树称为最优二叉树或者叫赫夫曼树。

构造赫夫曼树：

假设有n个权值，则构造出的赫夫曼树有n个叶子节点，n个权值分别设置为w1，w2,....wn,则赫夫曼树的构造规则为：

1.将w1,w2...看成是有n棵树的森林；

2.在森林中选择两个根节点的权值最小的树合并，作为一棵新树的左右子树，且新树的根节点权值为其左右子树根节点权值之和；

3.从森林中删除选取的两棵树，并将新树加入森林；

4.重复2、3步，直到森林中只剩一棵树为止，该树即为所求得的赫夫曼树。

实现：

以数组形式存储赫夫曼树节点，节点形态：

/**************************************************
构造赫夫曼树
by Rowandjj
2014/6/2
**************************************************/
#include<IOSTREAM>
using namespace std;

#define UINT_MAX 0xffffffff

typedef struct _BITREE_//二叉树
{
    int data;//存放节点的圈中
    struct _BITREE_ *lChild;
    struct _BITREE_ *rChild;
}Bitree,*pBitree;

typedef struct _HUFFMANTREE_//赫夫曼树
{
    unsigned int weight;
    unsigned int parent;
    unsigned int lChild;
    unsigned int rChild;
}HuffmanTree,*pHuffmanTree;

int iCount = 0;//叶子节点数
int iIndex = 1;//索引

//-----------------------------------------

void CreateBiTree(pBitree* pBitreeTemp);//创建二叉树
void CreatreArray(pHuffmanTree& pHuffmanTreeTemp,pBitree pBitreeTemp);//将二叉树每个节点的值作为权放进赫夫曼树中
pHuffmanTree InitHuffmanTree();//初始化赫夫曼树，
void CreateHuffmanTree(pHuffmanTree& pHuffmanTreeTemp);//创建赫夫曼树
int GetNode(pHuffmanTree& pHuffmanTreeTemp,int i);//获取赫夫曼树中位置0-i中值最小的节点的索引
void SelectNode(pHuffmanTree& pHuffmanTreeTemp,int i,int *m,int *n);//选择赫夫曼树数组中值最小的两个节点的索引（不包含已有父节点的节点）
void DestroyTree(pBitree* pBitreeTemp);
void DestroyHuffmanTree(pHuffmanTree& pHuffmanTreeTemp);
int main()
{
    int i;
    //创建二叉树
    pBitree pBitreeTemp;
    CreateBiTree(&pBitreeTemp);
    //初始化赫夫曼树
    pHuffmanTree pHuffmanTreeTemp = InitHuffmanTree();

    //初始化赫夫曼树的叶子节点的权
    CreatreArray(pHuffmanTreeTemp,pBitreeTemp);
    for(i = 1; i <= iCount ; i++)
    {
        cout<<pHuffmanTreeTemp[i].weight<<" ";
    }
    cout<<endl;
    //创建赫夫曼树
    CreateHuffmanTree(pHuffmanTreeTemp);
    for(i = 1; i <= 2*iCount-1 ; i++)
    {
        cout<<pHuffmanTreeTemp[i].weight<<" ";
    }
    cout<<endl;

    DestroyTree(&pBitreeTemp);
    DestroyHuffmanTree(pHuffmanTreeTemp);
    return 0;
}

void CreateBiTree(pBitree* pBitreeTemp)
{
    int data;
    cin>>data;
    if(data == -1)
    {
        return;
    }
    *pBitreeTemp = (pBitree)malloc(sizeof(Bitree));
    if(*pBitreeTemp == NULL)
    {
        return;
    }
    (*pBitreeTemp)->data = data;
    (*pBitreeTemp)->lChild = NULL;
    (*pBitreeTemp)->rChild = NULL;

    CreateBiTree(&(*pBitreeTemp)->lChild);
    CreateBiTree(&(*pBitreeTemp)->rChild);

    iCount++;
}
pHuffmanTree InitHuffmanTree()
{
    int num = 2*iCount - 1;//赫夫曼树的节点总数为：叶子节点数*2-1
    pHuffmanTree pTemp = (pHuffmanTree)malloc(sizeof(HuffmanTree)*(num+1));//0位不存
    if(pTemp == NULL)
    {
        return NULL;
    }
    for(int i = 0; i <= num; i++)
    {
        pTemp[i].lChild = 0;
        pTemp[i].rChild = 0;
        pTemp[i].parent = 0;
        pTemp[i].weight = 0;
    }
    return pTemp;
}
void CreatreArray(pHuffmanTree& pHuffmanTreeTemp,pBitree pBitreeTemp)
{
    if(pBitreeTemp == NULL || pHuffmanTreeTemp == NULL)
    {
        return;
    }
    pHuffmanTreeTemp[iIndex].weight = pBitreeTemp->data;
    iIndex++;
    CreatreArray(pHuffmanTreeTemp,pBitreeTemp->lChild);
    CreatreArray(pHuffmanTreeTemp,pBitreeTemp->rChild);
}
int GetNode(pHuffmanTree& pHuffmanTreeTemp,int i)
{
    int min = UINT_MAX;
    int flag;
    for(int j = 1; j <= i; j++)
    {
        if(pHuffmanTreeTemp[j].weight < min && pHuffmanTreeTemp[j].parent == 0)//已有父节点的不算
        {
            min = pHuffmanTreeTemp[j].weight;
            flag = j;
        }
    }
    pHuffmanTreeTemp[flag].parent = 1;//防止两次调用获取的索引相同
    return flag;
}
void SelectNode(pHuffmanTree& pHuffmanTreeTemp,int i,int *m,int *n)//m为序号小的那个
{
    *m = GetNode(pHuffmanTreeTemp,i);
    *n = GetNode(pHuffmanTreeTemp,i);

    int t;
    if(*m > *n)
    {
        t = *m;
        *m = *n;
        *n = t;
    }
}

void CreateHuffmanTree(pHuffmanTree& pHuffmanTreeTemp)
{
    if(pHuffmanTreeTemp == NULL)
    {
        return;
    }
    int m = 0,n = 0;
    for(int i = iCount+1;i <= 2*iCount-1; i++)
    {
        SelectNode(pHuffmanTreeTemp,i-1,&m,&n);
        pHuffmanTreeTemp[m].parent = pHuffmanTreeTemp[n].parent = i;
        //构造两个最小权重的节点的父节点
        pHuffmanTreeTemp[i].lChild = m;
        pHuffmanTreeTemp[i].rChild = n;
        pHuffmanTreeTemp[i].weight = pHuffmanTreeTemp[m].weight+pHuffmanTreeTemp[n].weight;
    }

}

void DestroyTree(pBitree* pBitreeTemp)
{
    if(*pBitreeTemp == NULL)
    {
        return;
    }
    if((*pBitreeTemp)->lChild)
    {
        DestroyTree(&(*pBitreeTemp)->lChild);
    }
    if((*pBitreeTemp)->rChild)
    {
        DestroyTree(&(*pBitreeTemp)->rChild);
    }
    free(*pBitreeTemp);
    *pBitreeTemp = NULL;
}

void DestroyHuffmanTree(pHuffmanTree& pHuffmanTreeTemp)
{
    if(pHuffmanTreeTemp)
    {
        free(pHuffmanTreeTemp);
    }
    pHuffmanTreeTemp = NULL;
}

测试：

图解构造过程：

1.首先将二叉树中的节点全部存到代表赫夫曼树的数组中，其余位置为0:

2.循环遍历该数组，每次找到最小权重的两个节点，之和作为其父节点的权重

3.循环一遍后，便得到赫夫曼树：