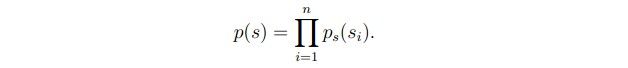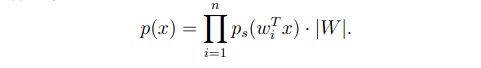机器学习 cs229学习笔记5 (ICA Independent components analysis)
(all is based on the stanford's open-course CS229 lecture 15)
因为对ICA理解得不是很深刻
在网上东搜西搜搜到一个牛人的bloghttp://www.cnblogs.com/jerrylead/
他也写了cs229的学习笔记系列,和我的一比较顿时我就自惭形秽了,不过既然都差不多快写完了,我也就继续坚持着吧
毕竟我的本意是给自己留个笔记,不过我也把他写的笔记download下来加深理解,学习了
==========================================================================
零.知识准备
概率密度函数和累积分布函数(cumulative distribution function, 缩写为 cdf)---这是概率论的基础知识了吧
其中概率密度函数的变换
也就是说如果我们有一个概率密度函数![]() ,如果有
,如果有![]() ,怎样求
,怎样求![]()
公式如下:其中|W|时矩阵W的行列式,W时A的逆矩阵
一.引例
这个问题的引例其实就是在cs229的第一节课上讲到的鸡尾酒问题
即两个人在酒会上同时讲话,而在房间不同位置的两个麦克风记录了他们的声音,要把两个声音分离出来
andrew ng当时给了一个svd的公式,但好像和lecture 15的关系不大
其实刚进大一的时候我就很无知地想过用函数去拟合声音,但是后来觉得声音是混杂的,所以也没继续想,想在想来真是===无知者无畏啊![]()
这样的问题不光出现在声音上,也出现在脑电波识别(meg)和图像处理(cv)等领域
二.思路
如果我们拿到一个混杂的声音,其实很难识别出其独立的部分(鸡尾酒问题中的两个独立部分就是两个人分别说话的声音)
而鸡尾酒问题中要两个麦克风的原因也在于此,就像人的双耳效应一样,两个麦克风记录的声音,每个独立部分的大小是不一样的
ica就是通过其中的差异来分离出其独立部分
我们知道矩阵其实是一种变换,而声音的重叠其实就是一种变换(考虑声音的在计算机中的储存方式,是以时间为轴的图像,图像上的高度对应声音的数据),
所以假设我们有两个源声音s1,s2,声音的叠加就是关于s1和s2的线性变换,用一个矩阵A表示这种变换,在鸡尾酒问题中,A是2*2的
所以![]() ,也就是我们麦克风记录到的两个混杂的声音
,也就是我们麦克风记录到的两个混杂的声音
ica就是通过找到A的逆矩阵从而还原源声音s的
同时,这种变换对于高斯分布的数据是无效的,因为变换在旋转时会造成歧义(貌似是这样,再看看)
三.算法
机器学习的东西很难不和概率扯上关系,所以照旧,我们的最大似然函数就是
可以推导出:
在此我们需要给出ps的定义,ps是数据的概率密度函数,而我们需要一个非高斯分布的概率密度函数,因此我们需要一个非高斯的概率分布函数
其实可以任意选择,只要符合概率分布函数的性质,这里我们选择了sigmoid函数作为概率分布函数,即:
![]()
这样log似然函数就变成了
其中m是训练样例数,n是参数数,对应带鸡尾酒问题中,m是离散的声音点的个数,n是麦克风(人)的个数
然后再通最大化似然函数我们就可以得到随机梯度上升算法的迭代式了(注意这里如果用batch gradient ascent没什么效果)
四.算法的不确定性(ambiguities)
1.源数据的顺序
ica可以分理出不同的独立成分,但是无法指出哪一个独立成分对应一个源数据,这是很好理解的
因为变换矩阵A可能会是一个permutation matrix,也就是说矩阵行于行之间交换顺序这不会影响矩阵的各种性质
幸运的是,这对大多数应用没有影响
2.还原数据的scaling
因为scaling是一维的线性变换,也就是说乘除一个常数,所以因为![]() ,我们只知道x,所以不能得到具体的A和s的scaling
,我们只知道x,所以不能得到具体的A和s的scaling
这在声音问题上的影响就是声音的大小,也是可以忽略的
五.代码
学习要用代码来加强,找了一些文章,发现基本上都是用fastICA的版本,是一个类似于神经网络的方法,略高端
最后给出一个基于最大似然的梯度上升算法的代码以及实验数据(matlab)
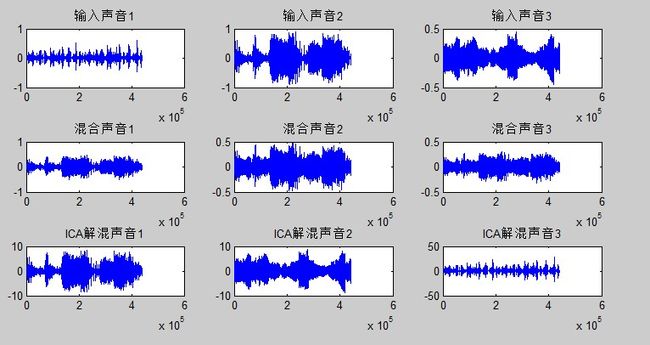
[n,m] = size(MixedS); chunk = 10; alpha = 1.5; W = eye(n); sss=MixedS; for iter=1:40 disp([num2str(iter)]); MixedS= MixedS(:,randperm(m)); for i=1:floor(m/chunk) Xc = MixedS(:,(i-1)*chunk+1:i*chunk); dW = (1 - 2./(1+exp(-W*Xc)))*Xc'+ chunk*inv(W'); W = W + alpha*dW; end end;实验效果(实验用的音频来自网上一个fastICA示范的数据,我就直接拿过来用了)
可以发现较好地还原了源数据,同时也体现了无法得到具体的scaling这个不确定性,音频强度明显减弱了,但是这对实验效果没什么影响
==========================================================================