图搜索-使用文本关键词搜索connected API subgraph

今天跟大家分享一篇挺有意思的关于graph searching的papar。这片paper来自FSE2012。有兴趣的童鞋请下载详读。《Searching Connected API Subgraph via Text Phrase》。

先简要介绍一下本文的作者。第一第二作者都来自港中文。Wing-Kwan Chan是在读博士生，主要方向是数据挖掘。Hong Cheng是该校的助理教授，在伊利诺伊大学厄本那香槟分校拿的博士学位，主要研究方向为数据挖掘。三作David Lo是新加坡管理大学的助理教授，博士毕业于新加波国立，主要研究方向是软件工程和数据挖掘。

我们在软件开发过程中一般都会去第三方的API库找我们所需要的API。这些第三方的API库经过充分的测试可以说非常可靠，能够帮助我们提高软件开发的效率，确保程序的质量。但是想找到合适的API并不那么容易，因为第三方的API库一般都非常庞大且非常的复杂，特别对于新手来说更是难上加难。以JSE1.6为例，它包含超过3100个类和28900个方法。找不找得到是一说，找到之后要了解API怎么用又是一个头疼的问题。


因此本文作者们就提出了一种方法，试图通过搜索推荐的技术为dev找到合适的API，并且给出API之间详细的调用关系，即API该怎么用。


主要的思想是：首先，使用一组关键词进行查询找到相关的API节点集合，然后使用提出的路径搜索算法从API节点集合中挖掘出一个最优的connected subgraph。这个subgraph中的节点表示的是与关键词集合相似度最高的API，边表示的是API之间的调用关系。

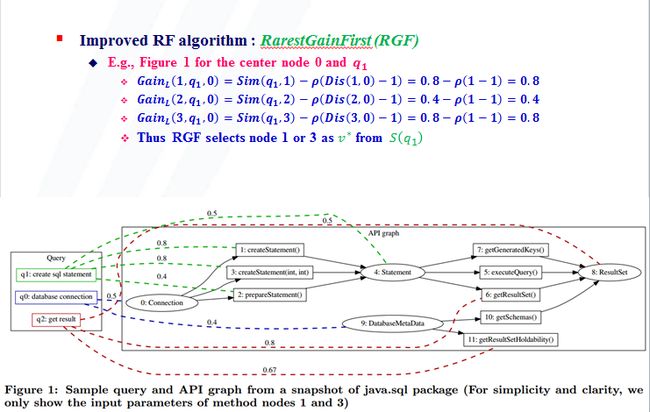
举个例子来说，假设我们API库就如Figure1中的右边方框所示，我们要从这个API库中找到我们所需要的API subgraph。左边是一个查询，它由3个短语组成，我们记为q0,q1,q2，查询目标可以理解成“连接数据库，处理SQL并返回结果”。图中的虚线连接了查询短语和它们在API库中的候选API节点，虚线上的值表示短语与节点之间的相似度。


我们希望从这个API库中找到的最优subgraph是0-->3-->4-->6, 第二个API取节点1,2,3都可以，我们这里以3为例。这个subgraph就告诉我们要完成“连接数据库，处理SQL并返回结果”只需要调用Connection中的createStatement()方法得到一个Statement对象，然后调用Statement中geResultSet()方法就可以得到查询结果。

要实现本文提出的方法需要解决两个问题：
1. API库非常大，那么其对应的API graph也就非常庞大，搜索空间也就非常庞大，时间复杂度会很高。
2. Subgraph中节点的连接依赖于节点之间的最短路径。为了快速生成Subgraph，有必要事先计算任意两API节点之间的最短路径，并存放到内存里。但这显然是不可能的，还是以JSE1.6为例，我们说到它共有超过30000个API节点（class+method），找到任意两点之间的最短路径并全部保存下来需要10.6GB的空间。

针对搜索空间过大的问题，他们提出了一种改进的greedy subgraph search algorithm；针对最短路径索引过大的问题，他们提出了一种新的索引模式（主要思想是只索引class节点）。

API库是由class/interface（用C来表示）和method/Constructor（用M来表示）构成的。节点之间存在着以下4种关系：
1. 继承关系：class A 继承 class B
2. 成员关系：Method A 是 Class B的成员方法
3. 输入关系：Class A的对象是Method A的输入参数
4. 输出关系：Method A 返回 Class B的对象
有了这4种关系，我们就可以定义API Graph了。所谓API Graph是由API库中所有的class和method节点构成的，如果两节点之间存在以上4种关系中的某一种，这两节点之间就有边相连。每个节点v表示成一个词袋BOW。以Figure1为例，节点0：createStatement()的词袋BOW={create, statement}。

接下来，我们要定义一下查询Q：一个查询Q由若干个查询短语Phrase组成。每个查询短语都可以表示成一个BOW（词袋）。以数据库查询的那个例子来说，Q有3个短语分别是q0=”database connection”; q1=”create sql statement” ; q2=”get result”。q0的词袋BOW={database, connection}, q1的词袋BOW={create, sql, statement}, q2的词袋BOW={get result}。


我们用Dice’s coefficient来度量查询关键词q和API graph中某一节点v的相似度。候选节点必须满足与关键词的相似度大于等于给定的阈值??。
【与Dice系数类似的有Jaccard系数，都是用来衡量两个集合之间的相似度，后者常用于IR（信息检索）】

当找到一个subgraph，如何来评价这个subgraph的好坏呢？本文提出了Gain指标。这一指标的大体思想是：subgraph中各节点与查询的累积相似度越高，则这个subgraph越好。对于每个查询phrase来说，都会从API graph找到一个与其相似度最高的节点，这些节点称为necessary节点，构成Vo，这些最高相似度之和就是公式（2）的分子。在subgraph中除了这些necessary之外的点都被称为dummy节点。Dummy节点数与phrase数之和作为公式（2）的分母，也就是说一个好的subgraph，其中的dummy节点应该尽可能的少。

有了上面这些定义之后，我们就可以给Searching API subgraph下一个最终定义：我们要找一个连接的subgraph。这个subgraph中每个节点和查询中某个phrase的相似度要大于等于给定的阈值。而且这个subgraph是所有候选的subgraph中Gain指标最高的。

当前能够有效搜索subgraph的一种方法是RarestFirst(简称RF)，它是在2009年的KDD上被提出的，主要是为了解决Team Formation问题：给定一个task，和一堆experts，每个expert擅长若干种skill，expert之间存在交流，即有关系网，但彼此交流需要一定的成本，那么我们需要找到一组experts，既要能够完成这个task又要使沟通成本最小。那么应用到本文的场景中，查询Q就相当于task，而（classes/methods）节点就相当于experts。

RF的总体思路为：

1.找到每个查询短语q的候选节点集；
2. 将候选节点集最小的q记为
3. 对于中每个节点c，以c为中心构造subgraph：从其他各个q的候选集中分别找出一个与c最近的节点v，选这几个最近距离中的最大值作为该subgraph的直径Rc。
4. 选择中Rc最小的节点c构造subgraph: 从其他各个q的候选集中分别找出一个与c最近的节点v，将path(c,v)添加到subgraph中。
我们直接举Figure1的例子来说明RF算法：假定相似度阈值=0.4，见下面两张PPT。

我们发现在RF算法中找到候选集之后，similarity就再也不起作用了，subgraph的构造只与distance有关。上例中我们需要随机的从{1,2,3}三个节点中选一个来构造路径，从相似度来考虑节点1,3的相似度要高于2，因此选择1或3更合理，但我们随机选择就会选择到2。


为了解决这个问题，本文提出了LocalGain来作为节点的选择指标。它既考虑了节点v与查询短语q的相似度Sim(q,v)，又考虑了节点v与中心节点c的距离Dist(v,c)。相似度越高，距离越近，则节点v的LocalGain越高。以v={1,2,3}, q=q1, c=0为例：

 

有了LocalGain之后，我们对RarestFirst进行改进得到RarestGainFirst，大致思想如下：
1. 找到每个查询短语q的候选节点集；
2. 将候选节点集最小的q记为
3. 对于 中每个节点c，以c为中心构造subgraph：从其他各个q的候选集中分别找出一个LocalGain最高的节点v，将path(c,v)添加到subgraph中。 
4. 选择Gain指标最高的subgraph作为搜索结果。

除了解决节点的选择问题外，我们还需要解决“多路径”问题，即两节点之间的最短路径不唯一。还是以figure1为例，Path(0,6)有3条可选的最短路径，RF和RGF中都是随机选择一条。我们希望算法给出的结果是唯一确定的且是最佳的，而不是有很高的不确定性。因此本文又给出了进阶的改进算法LocalRegionRefine(简称LRR)：在RGF的结果上使用Steiner Tree对结果进行优化。大致思想是：
1. 从RGF得到一个未优化的subgraph
2. 从这个subgraph中找出和每个查询短语q相似度最高的节点v，这些节点构成一个集合
3. 然后调用steiner Tree，用集合重新构造一个最优的subgraph
a) 构造两个集合，分别是covered和uncovered的集合，初始时我们选取中的一个节点放到covered集合中，把其他节点放到uncovered集合中。
b) 每次找两个结合之间的最短路径path(a,b)，然后把path(a,b)加到subgraph中，并把在uncovered中的那个点放到covered集合中，重复这个过程直到uncovered集合为空。
c) 返回subgraph.

LocalRegionRefine算法中我们需要给出两点之间的最短路径Path(a,b)，然后加入到subgraph中。因此我们需要事先计算好API graph中两两节点之间的最短路径，并保存在内存中。但正如一开始提到的，完全索引的空间开销过大。因此本文提出了一种能够有效压缩存储索引空间的索引模式，即Class-Only Path Indexing。提出该方法主要有两点依据：（1）API graph只包含class和method两种节点，class节点要比method节点少的多；（2）method节点之间没有直接的交互，与method节点毗邻的节点一定是class节点。

有了Class-Only的思想，API Graph就可以简化为Class Graph。Class Graph中两点之间边的权重是API Graph中这两点之间的最短距离，取值为{1,2}，也就是说两个class直接相连或中间由一个method相连。只有这两种情况。

本文为Class-Only索引模式设计了三种数据结构用于存储索引信息：
Parent[s][d]：在节点s到节点d的最短路径上d节点的前一个class 节点（s和d都是class节点）。
Adj[m]：API Graph上，method节点m毗邻的class节点集合。
Con[o][p]：连接class节点o和class节点p的method节点。如果o和p之间有多个method节点相连，则任意选一个即可。

利用上面讲到的三种结构存储最短路径信息之后，就能够非常方便的恢复API Graph中任意两点之间的最短路径。根据起止节点类型的不同，共有3种不同的情况：
1. 起止节点都是class节点
2. 一个class节点，一个method节点
3. 起止节点都是method节点


对于第2,3种情况，我们首先使用Adj[m]获得method节点毗邻的class节点集合。然后，对于第2种情况，求这个class集合与另一个class节点的最短路径；对于第3中情况来说，就转变为求两个class节点集合之间的最短路径。class节点之间的最短路径使用Parent[s][d]信息不断回溯就可恢复。

还是以Figure1为例，假设我们要恢复path(4,8)和path(5,11)
path(4,8)
节点4,8都是class节点，且在Class Graph中已经相邻，因此没有Parent[4][8]信息，因此我们通过con[4][8]获得连接两个class节点的method节点是节点5。所以得到path(4,8)=(4,5,8)。
path(5,11)
节点5,11都是method节点，因此先通过Adj[5]和Adj[11]确定与两节点毗邻class节点集合分别是{4,8}{9}，然后求两个集合之间的最短路径，发现Path(8,9)比path(4,9)要短，因此我们只需要在求出Path(8,9)即可。我们又发现8,9在Class Graph中已经相邻，通过con[8][9]确定连接两节点的method节点是方法10。至此我们就恢复了path(5,11)=（5,8,10,9,11）


至此本文所涉及的搜索方法全部介绍完毕。我认为虽然新设计的索引模式能够在很大程度上压缩索引空间，但如果API库足够大，大到即使只存储Class节点也无法存入内存，那这种方法也就不可行了。也就说新设计的方法其实是不可控的，它仍然是随着Class的数目成多项式增长的。因此，我们是否可以寻求一种更可控的索引模式是一个值得探讨的问题。


【本文的实验部分略】