深度学习（二十三）Maxout网络学习-ICML 2013

Maxout网络学习

原文地址：http://blog.csdn.net/hjimce/article/details/50414467

作者：hjimce

一、相关理论

   本篇博文主要讲解2013年，ICML上的一篇文献：《Maxout  Networks》，这个算法我目前也很少用到，个人感觉最主要的原因应该是这个算法参数个数会成k倍增加(k是maxout的一个参数)，不过没关系，对于我们来说知识积累才是最重要的，指不定某一天我们就需要用到这个算法，技多不压身。个人感觉Maxout网络和Dropout有很多相似的地方。

    本篇博文将从什么是maxout网络讲起，先解答maxout的源码层实现，因为很多人最感兴趣的还是算法要怎么实现，当然我也是这样的。我看文献，一般最在意的还是源码的实现，有的文献理论公式推导了十几页，结果5行代码搞定，我看到想哭，这也许就是我讨厌做学术研究的原因吧。知道了源码怎么实现后，我们简单啰嗦一下maxout相关的理论意义。

二、Maxout算法流程

1、算法概述

开始前我们先讲解什么叫maxout networks，等我们明白了什么叫maxout 网络后，再对maxout的相理论意义做出解释。Maxout是深度学习网络中的一层网络，就像池化层、卷积层一样等，我们可以把maxout 看成是网络的激活函数层，这个后面再讲解，本部分我们要先知道什么是maxout。我们假设网络某一层的输入特征向量为：X=（x1,x2,……xd），也就是我们输入是d个神经元。Maxout隐藏层每个神经元的计算公式如下：

 

上面的公式就是maxout隐藏层神经元i的计算公式。其中，k就是maxout层所需要的参数了，由我们人为设定大小。就像dropout一样，也有自己的参数p(每个神经元dropout概率)，maxout的参数是k。公式中Z的计算公式为：

 

权重w是一个大小为(d,m,k)三维矩阵，b是一个大小为(m,k)的二维矩阵，这两个就是我们需要学习的参数。如果我们设定参数k=1，那么这个时候，网络就类似于以前我们所学普通的MLP网络。

我们可以这么理解，本来传统的MLP算法在第i层到第i+1层，参数只有一组，然而现在我们不怎么干了，我们在这一层同时训练n组参数，然后选择激活值最大的作为下一层神经元的激活值。下面还是用一个例子进行讲解，比较容易搞懂。

为了简单起见，假设我们网络第i层有2个神经元x1、x2，第i+1层的神经元个数为1个，如下图所示：

(1)以前MLP的方法。我们要计算第i+1层，那个神经元的激活值的时候，传统的MLP计算公式就是：

z=W*X+b

out=f(z)

其中f就是我们所谓的激活函数，比如Sigmod、Relu、Tanh等。

(2)Maxout 的方法。如果我们设置maxout的参数k=5，maxout层就如下所示：

相当于在每个输出神经元前面又多了一层。这一层有5个神经元，此时maxout网络的输出计算公式为：

z1=w1*x+b1

z2=w2*x+b2

z3=w3*x+b3

z4=w4*x+b4

z5=w5*x+b5

out=max(z1,z2,z3,z4,z5)

所以这就是为什么采用maxout的时候，参数个数成k倍增加的原因。本来我们只需要一组参数就够了，采用maxout后，就需要有k组参数。

三、源码实现

ok，为了学习maxout源码的实现过程，我这边引用keras的源码maxout的实现，进行讲解。keras的网站为：http://keras.io/   。项目源码网站为：https://github.com/fchollet/keras。下面是keras关于maxout网络层的实现函数：

#maxout 网络层类的定义
class MaxoutDense(Layer):
    # 网络输入数据矩阵大小为(nb_samples, input_dim)
    # 网络输出数据矩阵大小为(nb_samples, output_dim)
    input_ndim = 2
   #nb_feature就是我们前面说的k的个数了，这个是maxout层特有的参数
    def __init__(self, output_dim, nb_feature=4,
                 init='glorot_uniform', weights=None,
                 W_regularizer=None, b_regularizer=None, activity_regularizer=None,
                 W_constraint=None, b_constraint=None, input_dim=None, **kwargs):
        self.output_dim = output_dim
        self.nb_feature = nb_feature
        self.init = initializations.get(init)

        self.W_regularizer = regularizers.get(W_regularizer)
        self.b_regularizer = regularizers.get(b_regularizer)
        self.activity_regularizer = regularizers.get(activity_regularizer)

        self.W_constraint = constraints.get(W_constraint)
        self.b_constraint = constraints.get(b_constraint)
        self.constraints = [self.W_constraint, self.b_constraint]

        self.initial_weights = weights
        self.input_dim = input_dim
        if self.input_dim:
            kwargs['input_shape'] = (self.input_dim,)
        self.input = K.placeholder(ndim=2)
        super(MaxoutDense, self).__init__(**kwargs)
    #参数初始化部分
    def build(self):
        input_dim = self.input_shape[1]

        self.W = self.init((self.nb_feature, input_dim, self.output_dim))#nb_feature是我们上面说的k。
        self.b = K.zeros((self.nb_feature, self.output_dim))

        self.params = [self.W, self.b]
        self.regularizers = []

        if self.W_regularizer:
            self.W_regularizer.set_param(self.W)
            self.regularizers.append(self.W_regularizer)

        if self.b_regularizer:
            self.b_regularizer.set_param(self.b)
            self.regularizers.append(self.b_regularizer)

        if self.activity_regularizer:
            self.activity_regularizer.set_layer(self)
            self.regularizers.append(self.activity_regularizer)

        if self.initial_weights is not None:
            self.set_weights(self.initial_weights)
            del self.initial_weights

    def get_output(self, train=False):
        X = self.get_input(train)#需要切记这个x的大小是(nsamples,input_num) 
        # -- don't need activation since it's just linear.
        output = K.max(K.dot(X, self.W) + self.b, axis=1)#maxout激活函数
        return output

看上面的代码的话，其实只需要看get_output()函数，就知道maxout的实现了。所以说有的时候，一篇文献的代码，其实就只有几行代码，maxout就仅仅只有一行代码而已：

output = K.max(K.dot(X, self.W) + self.b, axis=1)#maxout激活函数

下面在简单啰嗦一下相关的理论，毕竟文献的作者写了那么多页，我们总得看一看才行。Maxout可以看成是一个激活函数 ，然而它与原来我们以前所学的激活函数又有所不同。传统的激活函数：

比如阈值函数、S函数等。maxout激活函数，它具有如下性质：

1、maxout激活函数并不是一个固定的函数，不像Sigmod、Relu、Tanh等函数，是一个固定的函数方程

2、它是一个可学习的激活函数，因为我们W参数是学习变化的。

3、它是一个分段线性函数：

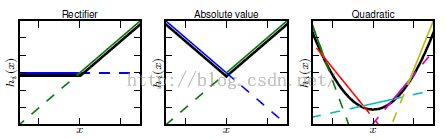
然而任何一个凸函数，都可以由线性分段函数进行逼近近似。其实我们可以把以前所学到的激活函数：relu、abs激活函数，看成是分成两段的线性函数，如下示意图所示：

　maxout的拟合能力是非常强的，它可以拟合任意的的凸函数。最直观的解释就是任意的凸函数都可以由分段线性函数以任意精度拟合（学过高等数学应该能明白），而maxout又是取k个隐隐含层节点的最大值，这些”隐隐含层"节点也是线性的，所以在不同的取值范围下，最大值也可以看做是分段线性的（分段的个数与k值有关）-本段摘自：http://www.cnblogs.com/tornadomeet/p/3428843.html

maxout是一个函数逼近器，对于一个标准的MLP网络来说，如果隐藏层的神经元足够多，那么理论上我们是可以逼近任意的函数的。类似的，对于maxout 网络也是一个函数逼近器。

定理1：对于任意的一个连续分段线性函数g(v)，我们可以找到两个凸的分段线性函数h1(v)、h2(v)，使得这两个凸函数的差值为g(v)：

参考文献：

1、《Maxout  Networks》

2、http://www.cnblogs.com/tornadomeet/p/3428843.html

**********************作者：hjimce   时间：2015.12.20  联系QQ：1393852684   地址：http://blog.csdn.net/hjimce   原创文章，版权所有，转载请保留本行信息（不允许删除）