《C++游戏开发》十七 游戏中的寻路算法(三):A*算法原理
本系列文章由七十一雾央编写,转载请注明出处。
http://blog.csdn.net/u011371356/article/details/10419981
作者:七十一雾央 新浪微博:http://weibo.com/1689160943/profile?rightmod=1&wvr=5&mod=personinfo
A*算法路径的评价公式为F=G+H
其中H为某个已达格子到目的地的估算距离,估算的方法有很多种,比如:
1、曼哈顿距离:即两点水平距离加上竖直距离。比如(x1,y1)到(x2,y2)的曼哈顿距离就是
|x2-x1|+|y2-y1|。
2、欧式距离:即两点之间的真实距离。(x1,y1)到(x2,y2)的欧式距离就是
sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1))。
3、切比雪夫距离:水平方向和竖直方向上的距离最大值。(x1,y1)到(x2,y2)的切比雪夫距离就是 max(|x2-x1|,|y2-y1|)。
下面采用曼哈顿距离来说,因为上一节提到的雾央学习的那篇文章是用这个的,有很多图,说起来方便。
首先准备一个开放列表和一个封闭列表。
开放列表用来保存待检验方格,封闭列表保存已经检验过的方格,即不再需要考虑的方格。
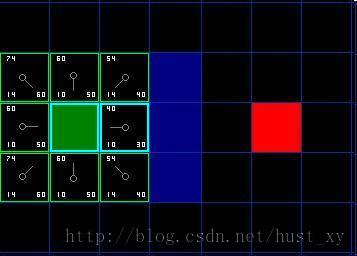
看这张图,绿色为出发点。
首先将绿色方格加入开放列表中,然后考察它周围的八个方格。我们将绿色方格从开放列表中删除掉,加入封闭列表中,因为我们不再需要检验它。同时把八个方格加入到开放列表中,他们将会是下一步考察的对象。
图中每个格子中有三个数字和一把钥匙形状的东东。
钥匙把指向的格子表示该格子的父节点,也即表示经过父节点来到该节点,它的作用是记录下路径。
我们的路径评估函数式F=G+H。
格子中的三个数字左上角的是F,左下角的是G,右下角的是H。
在绿色方格的上下左右四个格子的G值都是10,这是假定一个格子的路径长度是10,而它的四个对角的格子的G值是14,因为是通过对角线斜着到达的,所以是10的根号2倍,取14以方便计算。
看看绿色格子的右边的格子,清楚的标出了F,G,H。其中H=30,因为它离目的地红色格子只有三个格子的距离。注意,在估算距离的时候,是不用考虑障碍物什么的。
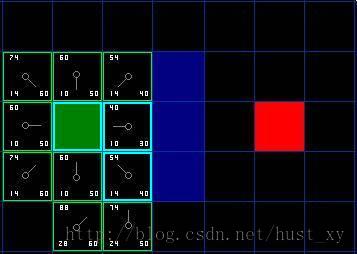
这时开放列表中有的格子就是绿色格子周围的那八个方格。
我们找出具有最小F值的,也就是绿色方格右边那个F=40,假定叫N。同上面一样的处理过程,将它移到封闭列表中去,把它周围的格子加入到开放列表中去。
这时候和上面情况就有些不同了:
一是有障碍物方块,这些方块我们不用理他们,我们只用考虑除了右面三块墙之外的五块格子。
二是有格子在封闭列表中,比如那个绿色格子。这种我们也不用管他们,因为封闭列表中的格子我们都已经处理过了。
三是有格子在开放列表中。对这些格子,原有的数据是从绿色格子到达他们的F值,现在又多了一条路径,从格子N到达他们,有可能会出现从N更近的情况,所以需要作出更新。即如果G值更小,就更新G值,并将他们的父结点从绿色格子替换为N。
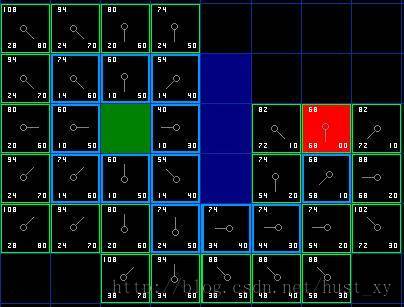
重复上述过程,再下一步会遇到在开放列表中有几个相同F值的情况,随便选择一个就好。
图中蓝色方框结点表示考察过的结点,即最终加入到了封闭列表中的结点。
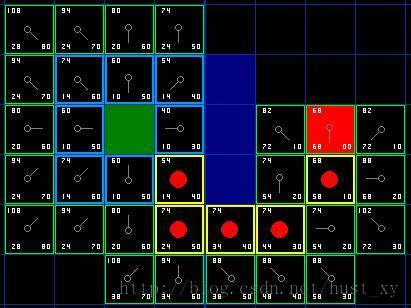
在最终到达红色结点时,就寻找到了最短的路径。
从红色开始,依次找到当前结点的父节点,直到到达绿色结点,就找到了最短路径。
当开放列表为空的时候,表示找不到路径,此时已经把所有能到达的格子都遍历了一遍。