LeetCode—Binary Tree Postorder Traversal 解题报告

转载请注明：http://blog.csdn.net/ict2014/article/details/17471257

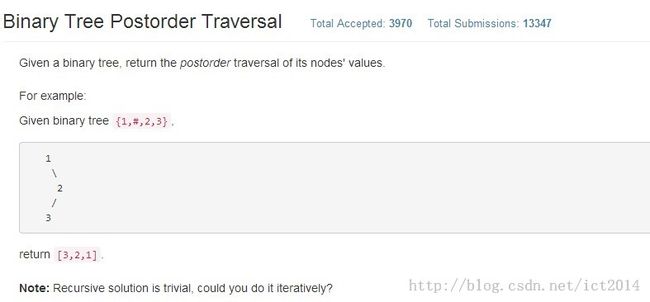
原题如下：

题目解析：

    此题是“二叉树的后序遍历”，一般最经典的模式就是递归方式，也是非常容易实现的一种。但是函数递归会耗费大量的栈空间，有可能会产生栈溢出错误。我的经验是，能用“循环”解决的事情，尽量不要用递归。对于这道题目，我会采用两种方法进行写代码。

    第一种就是：递归模式。先访问左子树，在访问右子树，然后访问根节点，程序的思路和这个是一样的，很方便实现。

    第二种就是：循环模式。这种方法比较难实现。由于必须先访问左子树，在访问右子树，才能访问根节点，因此，我们必须使用了一个堆栈进行保存数据。当访问到一个结点的时候，站在这个3叉路口的时候，我们有3种选择：进入左子树，进入右子树，从栈中抛出这个节点。我们应该如何做三种决定呢？也就是程序如何做三种决定呢？我们可以把“前一个删除的节点”保存起来，

      （一）做第一种决定可以如下实现：

                 左子树不为空、 左子树不等于“前一个删除的节点”、右子树不等于“前一个删除的节点”

      （二）做第二种决定可以如下实现：

                 第一种决定不满足、右子树不为空、右子树不等于“前一个删除的节点”

      （三）做第三种决定可以如下实现：

                 第一种决定不满足、第二种决定不满足

程序代码：

/**
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> post_order;
        if(root == NULL){
            return post_order;
        }
        
        PostorderVisitIterative(root, post_order);
        
        return post_order;
    }
    
    //recursive solution
    void PostorderVisitRecursive(TreeNode* root, 
                        vector<int>& result){
        if(root == NULL){
            return;
        }   
        //visit left child tree
        PostorderVisitRecursive(root->left, result);
        //visit right child tree
        PostorderVisitRecursive(root->right, result);
        //visit the root
        result.push_back(root->val);
    }
    
    //iterative solution
    void PostorderVisitIterative(TreeNode* root,
                                 vector<int>& result){
        //stack used for keeping the nodes
        stack<TreeNode*> datas;
        datas.push(root);
        TreeNode* top, *pre = root;
        while(!datas.empty()){
            top = datas.top();
            //the first condition
            //whether or not enter the left child tree
            if(top->left != NULL && 
               top->left != pre  && 
               top->right != pre){
                datas.push(top->left);
            }else{
                //the second condition
                //whether or not enter the right child tree
                if(top->right != NULL &&
                   top->right != pre){
                    datas.push(top->right);
                }else{
                    //the third condition
                    //pop the current node
                    result.push_back(top->val);
                    pre = top;
                    datas.pop();
                }
            }
        }
    }
};