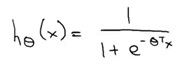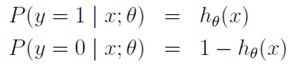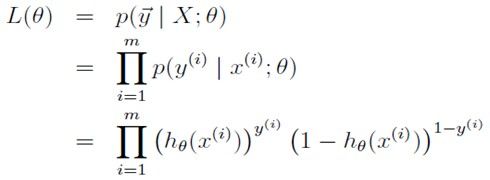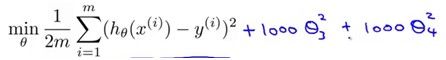Standford机器学习 逻辑回归(Logistic Regission)以及过拟合问题解决(Regularization)
1.分类问题
判断一封邮件是否为垃圾邮件,判断肿瘤是良性的还是恶性的,这些都是分类问题。在分类问题中,通常输出值只有两个(一般是两类的问题,多类问题其实是两类问题的推广)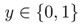 (0叫做负类,1叫做正类)。给定一组数据,标记有特征和类别,数据如(x(i),y(i)),由于输出只有两个值,如果用回归来解决会取得非常不好的效果。
(0叫做负类,1叫做正类)。给定一组数据,标记有特征和类别,数据如(x(i),y(i)),由于输出只有两个值,如果用回归来解决会取得非常不好的效果。
在良性肿瘤和恶性肿瘤的预测中,样本数据如下
上图是用线性归回得到的结果,那么可以选定一个阈值0.5,建立该模型后就可以预测:
如果训练数据是这样的
很明显,这样得到的结果是非常不准确的。线性回归中,虽然我们的样本输出数据都只有0和1,但是得到的输出却可以有大于1和小于0的,这不免有点奇怪。Logistic Regission的假设就是在0和1之间的。
2.Logistic Regression
我们希望的是模型的输出值在0和1之间,逻辑回归的假设,这个假设的推导在网易公开课的广义线性模型中有提到(分类的概率满足伯努利分布),这个以后再说
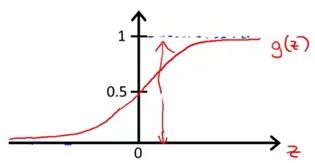
g(z)的函数图象是这样的一个S型曲线
现在只要假定,预测输出为正类的概率为H (x;theta)(因为根据该曲线,H是1的时候输出刚好是1),根据概率之和为1,可以得出如下式子
根据这个式子就可以来预测输出的分类了。和前面的线性回归一样,h(x)大于0.5的话,输出有更大的概率是正类,所以把它预测成正类。
从S型曲线可以看出,h(x)是单调递增的,如果h(x)>0.5则x*theta>0反之,x*theta<0,这个反映到x的坐标下,x*theta=0刚好是一条直线,x*theta>0和x*theta<0分布在该直线的两侧,刚好可以把两类样本分开。
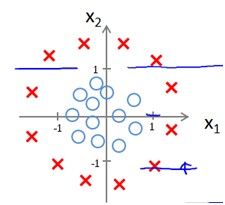
如果数据是下面这样的,很明显一条直线无法将它隔开
因此需要像多项式回归一样在x中添加一些feature,如
和前面一样y=theta0+theta1*x1+theta2*x2+theta3*x1^2+theta4*x2^2=0是一条曲线,y>0和y<0分布在该曲线两侧。得到了以上模型,只要用学习算法学习出最优的theta值就行了。
要学习参数theta,首先要确定学习的目标,即Cost Function。在线性回归中,我们选取的Cost Function是
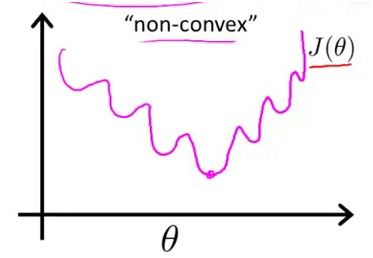
使得每个样本点到曲线的均方误差最小,要注意Logistic Regission中,h(x)带入J中得到的一个函数不是Convex的,形状如这样
因此这样的一个J(theta)不能用梯度下降法得到最优值,因为有多个极值点。
由于这个文类问题中,两类的概率满足伯努利分布,所以
这两个式子可以写成
给定一些样本点,可以使用极大似然估计来估计这个模型,似然函数为:
这里要求L(theta)的最大值,所以在前面添个负号就变成了求最小值,就可以用梯度下降法求解了。
观察J的前后两项,都是单调函数,因此J是Convex函数,目标就是要最小化这个函数,因此可以用梯度下降法。
求偏导之后发现这个式子和线性回归中的那个式子的相同的,要注意的是这里的h(theta)和线性回归中的是不一样的,需要区分。这样就得到了逻辑回归的分类模型!
3.过拟合问题以及解决方法(Regularization)
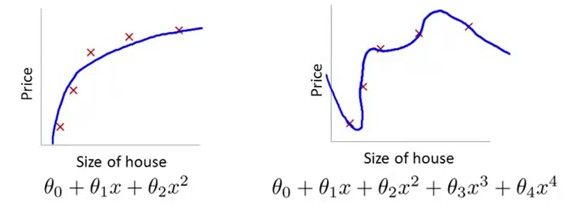
下面三个例子中,二是拟合的比较好的,一中有着较大的MSE,不是很好的模型,这种情况叫做 under fit,第三种情况虽然准确得拟合了每一个样本点,但是它的泛华能力会很差,这种情况叫做overfit。

在LogisticRegression中,上面三种情况对应的就是
Underfit和Overfit是实践过程中需要避免的问题,那么如何避免过拟合问题呢?
第一种方法就是减少feature,上面的例子中可以减少x^2这样的多项式项。
第二种方法就是这里要介绍的Regularization,Regularization是一种可以自动减少对预测结果没有影响(或影响较小)的feature的方法。
在下面这个例子中,如果我们学习得到theta3和theta4都是0或者非常接近于0,那么x的三次方项和四次方项这两个feature可以忽略,而得到的模型就是左边这个。
方法就是在原来的J后面加上惩罚项lambda*theta^2,这个例子中
优化过程中就会使得theta3和theta4尽量小,从而加惩罚因子的这些feature对模型的影响越小。
加上lambda后面的惩罚项(regularization parameter),这样就得到了Regularization后的新的模型
这里惩罚项式从1开始到n的,没有把0加进去,事实上,把0加进去对结果的影响非常小。
还有一个就是惩罚项系数lambda的选取问题,如果lambda选取的过大,那么最后的theta会接近于0,那么分割的曲线就会接近于直线,从而导致underfit(因为如果lambda非常非常大,要得到和前面的(h-y)相当大小的数值theta里面的所有元素就要很小),如果lambda过小,就相当于没有惩罚项,就是overfit。
求偏导后,梯度下降法中的更新式就变成了
最后还要说一下,对convex函数的优化,matlab提供了相应的优化工具,你可以把它看成是一个黑盒,你只需要把你的Cost Function和初始的theta值给他,并告诉它你需要用到什么样的优化方法,他就会帮你优化。下面是具体的使用方法:
% Set Options
options = optimset('GradObj', 'on', 'MaxIter', 400);
% Optimize
[theta, J, exit_flag] = ...
fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);
设置好选项,参数t会去调用你的costfunction,并用相应的你指定的方法优化相应的迭代次数。
总结:Logistic Regression和过拟合问题的解决方法是机器学习中非常重要的方法。貌似Google的搜索广告的摆放就是用了逻辑回归算法。
附fminunc的文档介绍
fminunc finds a local minimum of a function of several variables. X = fminunc(FUN,X0) starts at X0 and attempts to find a local minimizer X of the function FUN. FUN accepts input X and returns a scalar function value F evaluated at X. X0 can be a scalar, vector or matrix. X = fminunc(FUN,X0,OPTIONS) minimizes with the default optimization parameters replaced by values in the structure OPTIONS, an argument created with the OPTIMSET function. See OPTIMSET for details. Used options are Display, TolX, TolFun, DerivativeCheck, Diagnostics, FunValCheck, GradObj, HessPattern, Hessian, HessMult, HessUpdate, InitialHessType, InitialHessMatrix, MaxFunEvals, MaxIter, DiffMinChange and DiffMaxChange, LargeScale, MaxPCGIter, PrecondBandWidth, TolPCG, PlotFcns, OutputFcn, and TypicalX. Use the GradObj option to specify that FUN also returns a second output argument G that is the partial derivatives of the function df/dX, at the point X. Use the Hessian option to specify that FUN also returns a third output argument H that is the 2nd partial derivatives of the function (the Hessian) at the point X. The Hessian is only used by the large-scale algorithm. X = fminunc(PROBLEM) finds the minimum for PROBLEM. PROBLEM is a structure with the function FUN in PROBLEM.objective, the start point in PROBLEM.x0, the options structure in PROBLEM.options, and solver name 'fminunc' in PROBLEM.solver. Use this syntax to solve at the command line a problem exported from OPTIMTOOL. The structure PROBLEM must have all the fields. [X,FVAL] = fminunc(FUN,X0,...) returns the value of the objective function FUN at the solution X. [X,FVAL,EXITFLAG] = fminunc(FUN,X0,...) returns an EXITFLAG that describes the exit condition of fminunc. Possible values of EXITFLAG and the corresponding exit conditions are listed below. See the documentation for a complete description. 1 Magnitude of gradient small enough. 2 Change in X too small. 3 Change in objective function too small. 5 Cannot decrease function along search direction. 0 Too many function evaluations or iterations. -1 Stopped by output/plot function. -3 Problem seems unbounded. [X,FVAL,EXITFLAG,OUTPUT] = fminunc(FUN,X0,...) returns a structure OUTPUT with the number of iterations taken in OUTPUT.iterations, the number of function evaluations in OUTPUT.funcCount, the algorithm used in OUTPUT.algorithm, the number of CG iterations (if used) in OUTPUT.cgiterations, the first-order optimality (if used) in OUTPUT.firstorderopt, and the exit message in OUTPUT.message. [X,FVAL,EXITFLAG,OUTPUT,GRAD] = fminunc(FUN,X0,...) returns the value of the gradient of FUN at the solution X. [X,FVAL,EXITFLAG,OUTPUT,GRAD,HESSIAN] = fminunc(FUN,X0,...) returns the value of the Hessian of the objective function FUN at the solution X. Examples FUN can be specified using @: X = fminunc(@myfun,2) where myfun is a MATLAB function such as: function F = myfun(x) F = sin(x) + 3; To minimize this function with the gradient provided, modify the function myfun so the gradient is the second output argument: function [f,g] = myfun(x) f = sin(x) + 3; g = cos(x); and indicate the gradient value is available by creating an options structure with OPTIONS.GradObj set to 'on' (using OPTIMSET): options = optimset('GradObj','on'); x = fminunc(@myfun,4,options); FUN can also be an anonymous function: x = fminunc(@(x) 5*x(1)^2 + x(2)^2,[5;1]) If FUN is parameterized, you can use anonymous functions to capture the problem-dependent parameters. Suppose you want to minimize the objective given in the function myfun, which is parameterized by its second argument c. Here myfun is a MATLAB file function such as function [f,g] = myfun(x,c) f = c*x(1)^2 + 2*x(1)*x(2) + x(2)^2; % function g = [2*c*x(1) + 2*x(2) % gradient 2*x(1) + 2*x(2)]; To optimize for a specific value of c, first assign the value to c. Then create a one-argument anonymous function that captures that value of c and calls myfun with two arguments. Finally, pass this anonymous function to fminunc: c = 3; % define parameter first options = optimset('GradObj','on'); % indicate gradient is provided x = fminunc(@(x) myfun(x,c),[1;1],options) See also optimset, fminsearch, fminbnd, fmincon, @, inline. Reference page in Help browser doc fminunc