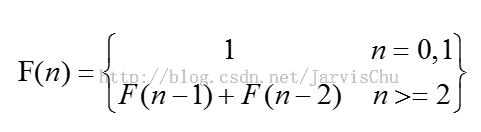算法入门2:分治算法(上)
上一篇中讲解了算法的基本概念,算法许许多多,按照算法基本思想,大致可分为如下几类:分治算法、贪心算法、动态规划、回溯法、分支限界、概率算法和随机算法等等。这一篇讲解分治算法。
分治算法
分治即分而治之。一个问题规模过大不容易直接解决,就可以划分成许多小问题,如果小问题不容易求解,那么可以再划分成规模更小的问题,直到规模小到很容易解决为止,解决这些小问题,再将小问题的解合并成大问题的解。这就是分治算法的基本思想。
至于小问题的规模到底划分多大,这是没有规定的,依实际情况而定。小问题的规模可以是相等的,也可以是不相等的。可以分成简单的2个小问题,当然也可以分成多个小问题。
分治算法常用的实现方法是递归。因为分治就是将大问题不断划分成小问题,递归的解决小问题,再合并小问题的解就可以得到问题的解。
递归
递归,就是在函数内部调用本函数自身。形式如下
void foo()
{
//...
foo(); //递归
//...
}
下面举几个递归的典型例子。
阶乘
n! = n*(n-1)! 这就是一个递归
如果F(n)代表求解n!,那么F(n) = n * F(n-1)
int f(int n)
{
if(n==1)
{
return 1;
}
return n*f(n-1);
}
Fibonacci数列
其定义为
int f(int n)
{
if(n==0 || n==1)
return 1;
return f(n-1)+f(n-2);
}
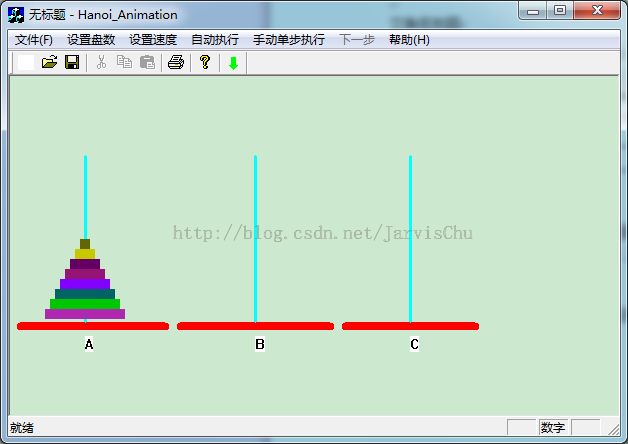
汉诺塔问题
A,B,C三个塔座,将A上的N个盘子移动到C上,保证大的盘子不会放在小的盘子上。
//直接将塔座from最上面的盘子移动到塔座to上
void move(char from,char to)
{
cout<<"Move:"<<from<<" -->"<<to<<endl;
}
//n个盘子,从A移动到C,借助B
void hanoi(int n,char A,char B,char C)
{
if(n>0)
{
hanoi(n-1,A,C,B); //首先将A中上面的n-1个盘子,从A移动到B,借助C
move(A,C); //然后将A中最下面的盘子直接移动到C
hanoi(n-1,B,A,C); //最后,将B上的n-1个盘子移动到C,借助A
}
}
int main()
{
hanoi(3,'A','B','C');
return 0;
}
PS: 博主用MFC实现了一个汉诺塔的动画效果。如有兴趣可留邮箱索要源码。(代码中还存在bug,但基本功能可用)可以单步运行移动,也可以自动执行移动。
全排列问题
输出N个数的全排列的结果。
比如当N=3,三个数为1,2,3时 ,全排列为:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
N个数的全排列为Perm(N),也就是等于把N个数分别替换到第一位时的所有排列,即Perm(N) = 1_Perm(N-1) + 2_Perm(N-1)+…+N_Perm(N-1)
以上面的为例,Perm(N)就是1,2,3的全排列,1_Perm(N-1)就是 1,2,3 和 1,3,2
2_Perm(N-1)就是2,1,3和2,3,1。
同理可以对Perm(N-1)再递推到Perm(N-2)
下面是代码,有详细的注释
/************************************************************************
* 名 称:Perm.cpp
* 功 能:分治算法案例:使用递归解决全排列问题(对n个数进行全排列)
* 作 者:JarvisChu
* 时 间:2013-11-1
************************************************************************/
#include <iostream>
using namespace std;
const int N=5; //常量,数组(序列)大小
/*----------------------------------------------------------------------------------
* 功 能: 交换两个数
* 参 数: a,b为要交换的元素
* 返 回:无
------------------------------------------------------------------------------------*/
void swap(int& a,int& b)
{
int tmp = a;
a=b;
b=tmp;
}
/*----------------------------------------------------------------------------------
* 功 能: 输出数组arr中,从arr[start]到arr[end]的全排列
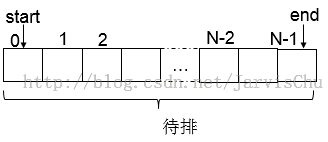
* 参 数: arr: 要全排列的数组
start: 要全排列数组段的起始位置下标,数组arr中 0到start-1位置已经排好
end: 要全排列的数组段的结束位置下标,arr[start]到arr[end]为待排数组段
* 返 回:无
------------------------------------------------------------------------------------*/
void Perm(int* arr,int start,int end)
{
if(start == end) //起点和终点位置重合,只剩最后一个元素了,说明arr已经全部排好了,此时输出结果
{
for(int i=0;i<N;++i)
cout<<arr[i]<<" ";
cout<<endl;
}
else //有数据要排列
{
for(int j=start;j<=end;++j)
{
swap(arr[start],arr[j]);//将j位置的数,放到start位置
Perm(arr,start+1,end); //递归排序
swap(arr[start],arr[j]);//交换回来
}
}
}
int main()
{
int data[N];
for(int i=0;i<N;i++)
{
data[i] = i+1; //N个数,从1到N
}
Perm(data,0,N-1);
return 0;
}
代码的图解:
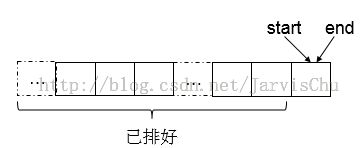
数组arr中 0到start-1位置已经排好, arr[start]到arr[end]为待排数组段。
初始时,start=0,end=N-1,说明要把arr[0]到arr[N-1]全排列输出
如果start==end,说明待排的长度为0,要么是前面的已经全部排好了,要么就是数字长度为0,总之直接输出结果就好
否者,说明待排的长度不为0。要排列arr[start]到arr[end],方法就是分别把每个元素放到start位置,来一次交换
交换后如图
交换后,在对递归排列start-1 到end位置
递归结束后,还需要把start和j的位置再调换回来,以便后面start和j+1的位置进行调换。
下一篇继续讲解分治算法的其他几个案例。
转载本文请注明作者和出处
作者 :JarvisChu
出处:http://blog.csdn.net/jarvischu