opengl学习笔记(五)——绘制复杂图形

本小节的代码参考了

http://www.cppblog.com/doing5552/archive/2009/01/08/71532.html里的内容。

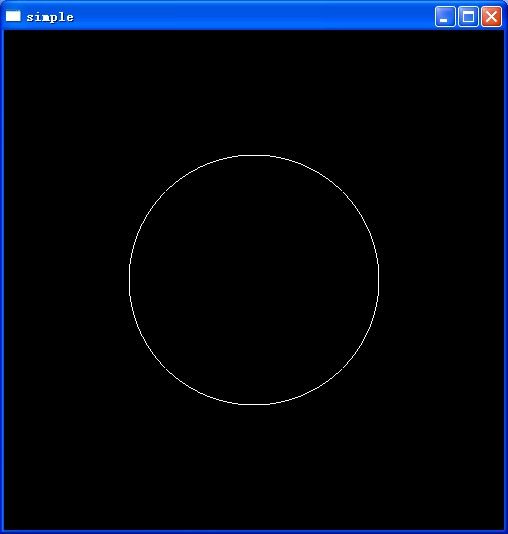
1、用正多边形模拟一个圆,主要思想是求出把圆n等分的各个顶点坐标，然后连线即可。第一个顶点的坐标为(R,0)。

核心代码如下:

#include <math.h>
const int n = 20;
const GLfloat R = 0.5f;
const GLfloat Pi = 3.1415926536f;
void display(void)
{
     int i;
     glClear(GL_COLOR_BUFFER_BIT);
     glBegin(GL_LINE_LOOP);
     for(i=0; i<n; ++i)
         glVertex2f(R*cos(2*Pi/n*i), R*sin(2*Pi/n*i));
     glEnd();
     glFlush();
}

下图1是n=20的结果。

下图2是n=200的结果

2、画一个五角星，效果如下所示

代码思路是设正五边形边长为1。

圆半径为R，圆心O为坐标原点，

显然有R=0.5/sin36°;

第一个顶点A的坐标为(0,R)，

则B点的横坐标bx=R*cos18°,纵坐标by=R*sin18°

C点的横坐标cx=1/=0.5,纵坐标cy=-R*sin54°

DE两点和BC关于y轴对称，所以最终的代码如下:

#include <math.h>
const GLfloat Pi = 3.1415926536f;
const GLfloat arc= Pi/180;  //1度角所对应的弧度
void display(void)
{
	const GLfloat r = 0.5f/sin(36 * arc) ;
	GLfloat bx = r * cos(18 * arc);
	GLfloat by = r * sin(18 * arc);
	GLfloat cx = 0.5f;
	GLfloat cy = -r * sin(54 * arc);
	//各定点坐标
	GLfloat
		A[2] = { 0, r },
		B[2] = { bx, by },
		C[2] = { cx, cy },
		D[2] = { -cx, cy },
		E[2] = { -bx, by };
	
	// 按照A->C->E->B->D->A的顺序，可以一笔将五角星画出
	glClear(GL_COLOR_BUFFER_BIT);
	glBegin(GL_LINE_LOOP);
	glColor3f(1.0, 0.0, 0.0);
	glVertex2fv(A);
	glVertex2fv(C);
	glVertex2fv(E);
	glVertex2fv(B);
	glVertex2fv(D);
	glEnd();
	glFlush();
}

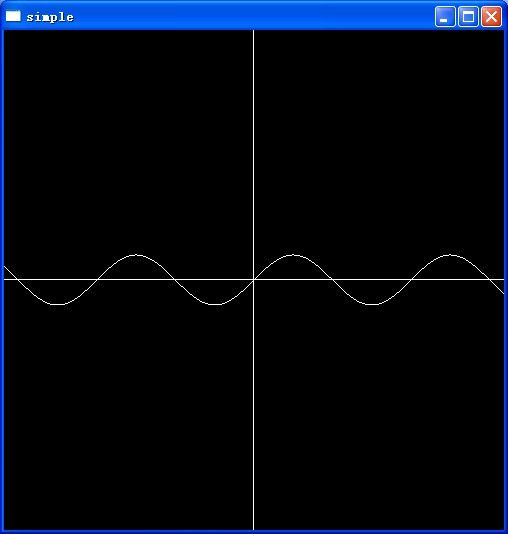
3、画正弦函数图形
代码如下:

/*
由于OpenGL默认坐标值只能从-1到1，（可以修改，但方法留到以后讲）
所以我们设置一个因子factor，把所有的坐标值等比例缩小，
这样就可以画出更多个正弦周期
试修改factor的值，观察变化情况
*/

#include <math.h>
const GLfloat factor = 0.1f;  //缩放因子，将普通正弦函数的图像缩小10倍画到屏幕上。
void display(void)
{
	GLfloat x;
	glClear(GL_COLOR_BUFFER_BIT);
	glBegin(GL_LINES);
	glVertex2f(-1.0f, 0.0f);
	glVertex2f(1.0f, 0.0f);         // 以上两个点可以画x轴
	glVertex2f(0.0f, -1.0f);
	glVertex2f(0.0f, 1.0f);         // 以上两个点可以画y轴
	glEnd();
	
	//用描点法画出缩放后的正弦函数图像
	glBegin(GL_LINE_STRIP);
	for(x=-1.0f/factor; x<1.0f/factor; x+=0.01f)
	{
		glVertex2f(x*factor, sin(x)*factor);
	}
	glEnd();
	glFlush();
}

运行结果如下: