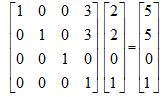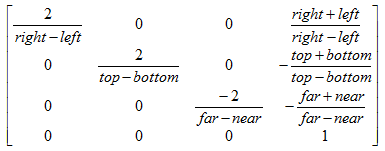Android OpenGL ES(四)----调整屏幕的宽高比

1.宽高比问题

我们现在相当熟悉这样一个事实，在OpenGL里，我们要渲染的一切物体都要映射到X轴和Y轴上[-1，1]的范围内，对于Z轴也一样。这个范围内的坐标被称为归一化设备坐标，其独立于屏幕实际尺寸或形状。

不幸的是，因为它们独立于实际的屏幕尺寸，如果直接使用它们，我们就会遇到问题，例如在横屏模式下被压扁的桌子。

假设实际的设备分辨率以像素为单位是1280*720，这在新的Android设备上是一个常用的分辨率。为了使讨论更加容易，让我们也暂时假定OpenGL占用整个显示屏。

如果设备是在竖屏模式下，那么[-1,1]的范围对应1280像素高，却只有720像素宽。图像会在X轴显得扁平，如果在横屏模式，同样的问题也会发生在Y轴上。

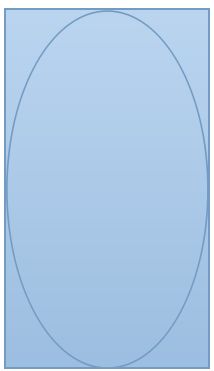
归一化设备坐标假定坐标空间是一个正方形，如下图所示：

然而，因为实际的视口可能不是一个正方形，图像就会在一个方向上被拉伸，在另一个方向上被压扁。在一个竖屏设备上，归一化设备坐标上定义的图像看上去就是在水平方向上被压扁了：

       

在横屏模式下，同样的图像就在另一个方向上看起来被压扁的。

2.适应宽高比

我们需要调整坐标空间，以使它把屏幕的形状考虑在内，可行的一个方法是把较小的范围固定在[-1,1]内，而按屏幕尺寸的比例调整较大的范围。

举例来说，在竖屏情况下，其宽度是720，而高度是1280，因此我们可以把宽度范围限定在[-1,1]，并把高度范围调整为[-1280/720,1280/720]或[-1.78,1.78]。同理在横屏模式情况下，把高度范围设为[-1.78,1.78]，而把高度范围设为[-1,1]。

通过调整已有的坐标空间，最终会改变我们可用的空间。

通过这个方法，不论是竖屏模式还是横屏模式，物体看起来就都一样了。

3.使用虚拟坐标空间

调整坐标空间，以便我们把屏幕方向考虑进来，我们需要停止直接在归一化设备坐标上工作，遥开始在虚拟坐标空间里工作。接下来，我们需要找到某种可以把虚拟空间坐标转化回归依化设备坐标的方法，让OpenGL可以正确的渲染它们。这种转换应该把屏幕方向计算在内，以使图像在竖屏模式和横屏模式看上去都一样。

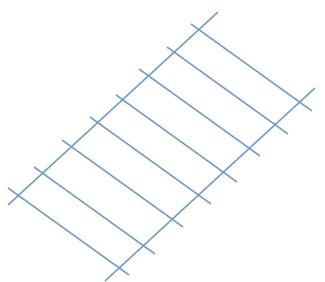
我们想要进行的操作叫作正交投影。使用正交投影，不管多远或者多近，所有物体看上去大小总是相同的。为了更高的理解这种投影是做什么的，想象一下，在我们的场景中有一个火车轨道，直接从空中俯瞰，这些轨道看起来是这样的：

还有一种特殊类型的正交投影，被称为等轴测投影，它是从侧角观察一种正交投影。正如在一些城市模拟和策略游戏中看到的，这种类型的投影能用来重新创建一个经典的三维角。

当我们使用正交投影把虚拟坐标变换回归化设备坐标时，实际上定义了三维世界内部的一个区域。在这个区域内的所有东西都会显示在屏幕上，而区域外的所有东西都会被剪裁掉。

利用正交投影矩阵改变立方体的大小，以使我们可以在屏幕上看到或多或少的场景。我们也能改变立方体的形状弥补屏幕的宽高比的影响。

4.线性代数基础

OpenGL大量使用了向量和矩阵，矩阵的最重要的用途之一就是建立正交和透视投影。其原因之一是，从本质上来说，使用矩阵做投影只涉及对一组数据按顺序执行大量的加法和乘法，这些运算在现代GPU上执行的非常快。

4.1向量

一个向量是一个有多个元素的一维数组。在OpenGL里，一个位置通常是一个四元素向量，颜色也一样。我们使用的大多数向量一般都有四个元素。在下面的例子中， 我们可看到一个位置向量，它有一个X，一个Y，一个Z，一个W分量。

4.2矩阵

一个矩阵是一个有多个元素的二维数组。在OpenGL里，我们一般使用矩阵作向量投影，如正交或者透视投影，并且也用它们旋转物体，平移物体以及缩放物体。我们把矩阵与每个要变换的向量相乘可实现这些变换。下面就是一个矩阵：

4.3矩阵与向量的乘法

要让矩阵乘以一个向量，我们把矩阵放在左边，向量放在右边。如下：

规则就是矩阵第一行乘以向量第一列，以第一行为例：矩阵第一行第一个元素乘以向量第一列第一个元素，加上矩阵第一行第二个元素乘以向量第一列第二个元素，加上矩阵第一行第三个元素乘以向量第一列第三个元素，加上矩阵第一行第四个元素乘以向量第一列第四个元素。矩阵二，三，四行同理。

4.4单位矩阵

单位矩阵如下：

之所以被称为单位矩阵，是因为这个矩阵乘以任何向量总是得到与原来相同的向量。就像把任何数字乘以1会得到原来的数字一样。

4.5平移矩阵

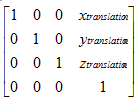
既然理解了单位矩阵，让我们看一个非常简单的矩阵类型---平移矩阵。它在OpenGL里十分常用。使用这种类型的矩阵，我们可以把一个物体沿着指定的距离移动。这个矩阵和单位矩阵差不多，但在右侧指定了三个额外的元素：

让我们盾一个位置（2，2）的例子，这个位置Z默认是0，W默认是1.我们把这个向量沿X轴平移3，沿Y轴也平移3，因此，把Xtranslation赋值为3，Ytranslation赋值为3。结果如下：

这个位置正是我们所期望和（5，5）。

5.正交投影

要定义正交投影，我们将使用Android的Matrix类，它在android.opengl包中。这个类有一个称为orthoM()的方法，它可以为我们生成一个正交投影。

我们来看一下orthoM()参数：

orthom(float[] m,int mOffset,float left,float rigth,float bottom,float top,float near,float far)

float[] m：目标数组，这个数组长度至少有16个元素，这样它才能存储正交投影矩阵。

int mOffset：结果矩阵起始的偏移值。

float left：X轴的最小范围。

float right：X轴的最大范围。

float bottom：Y轴的最小范围。

float top：Y轴的最大范围。

float near：Z轴的最小范围。

float far：Z轴的最大范围。

当我们调用这个方法的时候，它应该产生下面的正交投影矩阵：

这个正交投影矩阵会把所有在左右之间，上下之间和远近之间的事物映射到归一化设备坐标中从-1到1的范围，在这个范围内所有事物在屏幕上都是可见的。

主要的区别就是Z轴有一个负值符号，它的效果是反转Z坐标。这就意味着，物体离得越远，Z坐标的负值会越来越小。之所以这样完全是历史和传统的原因。

6.左手与右手坐标系统

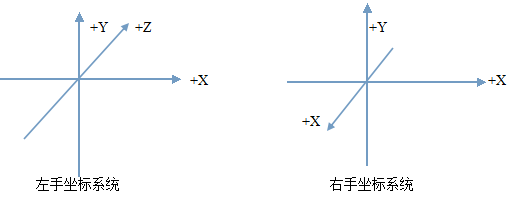
为了更好的理解Z轴问题，我们需要理解左手坐标系统与右手坐标系统之间的区别。想知道一个坐标系统是左手的还是右手的，你拿出一只手，把大拇指指向X轴正值方向，然后把食指指向Y轴正值方向。

现在，把你的中指指向Z轴。如果你需要用左手做这些，那你看到的就是一个左手坐标系统；如果你需要用右手，那你看到的就是一个右手坐标系统。把你的中指指向Z轴，记住要把大拇指指向X轴方向，食指指向Y轴正值方向。如下图：

其实左手还是右手选择都没关系，只是一个简单的转换。归一化设备坐标使用的是左手坐标系统，而在OpenGL的早期版本，默认使用的确实右手坐标系统，其使用Z的负值增加表示距离增加。这就是为什么Android的Matrix会默认生成反转Z的矩阵。

7.更新程序

7.1更新着色器

修改前一章的顶点着色器中的代码如下：

uniform mat4 u_Matrix;

attribute vec4 a_Position;    
attribute vec4 a_Color;
varying vec4 v_Color;
void main()                    
{
    v_Color=a_Color;
    gl_Position = u_Matrix*a_Position;
    gl_PointSize = 10.0;
}   

我们这里添加了一个新的uniform定义的“u_Matrix”，并把它定义为一个mat4类型，意思是这个uniform代表一个4*4的矩阵。更新位置负值那一行：

gl_Position =u_Matrix*a_Position;

我们没有传递数组中定义的位置，而是传递那个位置与一个矩阵的乘积。它意味着顶点数组不用再被翻译为归一化设备的坐标了，其将被理解为存在于这个矩阵所定义的虚拟坐标空间中。这个矩阵会把坐标从虚拟坐标空间变化回归一化设备坐标。

7.2添加矩阵数组和一个新的uniform

打开上一节的LYJRenderer添加成员变量：

private static final String U_MATRIX="u_Matrix";

我们还需要一个顶点数组存储矩阵：

private final float[] projectionMatrix=new float[16];

我们也需要一个整型值用于保存那个矩阵uniform的位置：

private int uMatrixLocation;

然后我们只需要在onSurfaceCreated()中加入如下代码：

uMatrixLocation=GLES20.glGetUniformLocation(program,U_MATRIX);

7.3创建正交投影矩阵

更新onSurfaceChanged()，在GLES20.glViewport()调用后面加入如下代码：

final float aspectRatio=width>height?(float)width/(float)heigth:(float)height/(float)width;

if(width>height){

orthoM(projectionMatrix,0,-aspectRatio,aspectRatio,-1f,1f,-1f,1f);

}else{

orthoM(projectionMatrix,0,-1f,1f,-aspectRatio,aspectRatio,-1f,1f);

}

这段代码会创建一个正交投影矩阵，这个矩阵会把屏幕的当前方向计算在内。注意在Android中不只有一个Matrix类，因此你要确保导入了android.opengl.Matrix。

我们首先计算了宽高比，它使用宽和高中的较大值除以宽和高的较小值。不管是竖屏还是横屏，这个值都一样。

7.4传递矩阵给着色器

在LYJRenderer中的onDrawFrame()中，我们在glClear()调用之后加入如下代码：

GLES20.glUniformMatrix4fv(uMatrixLocation,1,false,projectionMatrix,0);