BM算法学习

 

     BM算法全称为Boyer-Moore算法，与KMP算法相似是一种精确地模式匹配算法。一般来说比KMP算法更加高效。

   

与KMP算法比较

     相似点：都是寻找模式串自身的规律，在匹配失效时获得最大的跳转距离；

     不同点：实际操作中KMP算法是从左到右进行比较，而BM算法是从右到左。这就决定了在寻找规律的过程中，KMP算法的核心是寻找子串的相同前缀，而BM算法是寻找相同的后缀。

        KMP算法的核心请参见之前的博文《KMP算法学习》：http://blog.csdn.net/myjoying/article/details/7947119

        BM算法的核心是两条启发式规则：坏字符规则和好后缀规则。

 

坏字符规则

       所谓坏字符就是在比较过程中发现的第一个不匹配的字符。如下图中的红色字符。

        T： a  b  c d  a  b  c  a  b

        P：   d  a  b c a  b

 

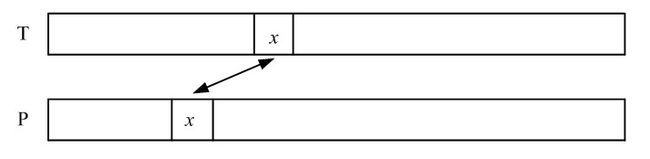
      坏字符规则：在任意字符x处发生失配时，在模式串P中找到与T中x左最近的x字符位置。并将找到的x移动到与T中x对齐。

       

      情况1：P中存在这样x，则将两个x对齐，重新比较；

        

      情况2：P中不存在这样的x，则将模式串P整个移动到T中x位置之后的位置对齐。

 

      

好后缀规则

       所谓好后缀就是在一次比较过程中模式串与目标串相匹配的后缀。如下图中的绿色字符串。

         T： a  b  c d  a  b  c  a  b

         P：  d  a  b c  a  b

        好后缀规则：如果程序匹配了一个好后缀,并且在模式中还有另外一个相同的后缀,那把下一个后缀移动到当前后缀位置。

        

        情况1：模式串中存在与好后缀完全匹配的子串，则将最靠右的那个子串移动到与T中好后缀对应位置，继续比较。

         

 

        情况2：在模式串中不存在与好后缀完全匹配的好后缀，则在好后缀子串中寻找与模式串前缀完全匹配的最长后缀。

         

移动距离

      BM算法存在两条移动规则，包括坏字符和好后缀规则。在每次失配时模式串移动的距离取两者最大距离移动。

 

 

代码分析（转）

 

BM算法子串比较失配时，按坏字符算法计算模式串需要向右移动的距离，要借助BmBc数组。

注意BmBc数组的下标是字符，而不是数字。

BmBc数组的定义，分两种情况。

1、 字符在模式串中有出现。如下图，BmBc[‘k’]表示字符k在模式串中最后一次出现的位置，距离模式串串尾的长度。

2、 字符在模式串中没有出现：，如模式串中没有字符p，则BmBc[‘p’] = strlen(模式串)。

BM算法子串比较失配时，按好后缀算法计算模式串需要向右移动的距离，要借助BmGs数组。

BmGs数组的下标是数字，表示字符在模式串中位置。

BmGs数组的定义，分三种情况。

1、 对应好后缀算法case1：如下图：i是好后缀之前的那个位置。

2、 对应好后缀算法case2：如下图所示：

3、 当都不匹配时，BmGs[i] = strlen（模式串）

在计算BmGc数组时，为提高效率，先计算辅助数组Suff。

Suff数组的定义：suff[i] = 以i为边界, 与模式串后缀匹配的最大长度，即P[i-s...i]=P[m-s…m]如下图：

 

在计算BmGc数组时，为提高效率，先计算辅助数组Suff。

Suff数组的定义：suff[i] =以i为边界,与模式串后缀匹配的最大长度，即P[i-s...i]=P[m-s…m]如下图：

 

用Suff[]计算BmGs的方法：

1） BmGs[0…m-1] = m；（第三种情况）

2）计算第二种情况下的BmGs[]值：

for (i = m - 1; i >= 0; --i)  
		
	if (suff[i] == i + 1)  
			
		for (; j < m - 1 - i; ++j)  
				
			if (bmGs[j] == m)  
					
				bmGs[j] = m - 1 - i; 

 

3）计算第一种情况下BmGs[]值，可以覆盖前两种情况下的BmGs[]值：

 

for (i = 0; i <= m - 2; ++i)  
					
	bmGs[m - 1 - suff[i]] = m - 1 - i;

 

 

如下图所示：

Suff[]数组的计算方法。

常规的方法：如下，很裸很暴力。

Suff[m-1]=m；
for（i=m-2；i>=0；--i）{
   q=i；
   while（q>=0&&P[q]==P[m-1-i+q]）
   --q；
  Suff[i]=i-q；
}

 

有聪明人想出一种方法，对常规方法进行改进。基本的扫描都是从右向左。改进的地方就是利用了已经计算得到的suff[]值，计算现在正在计算的suff[]值。

如下图所示：

i 是当前正准备计算的suff[]值得那个位置。

f 是上一个成功进行匹配的起始位置（不是每个位置都能进行成功匹配的，  实际上能够进行成功匹配的位置并不多）。

q 是上一次进行成功匹配的失配位置。

如果i在q和f之间，那么一定有P[i]=P[m-1-f+i]；并且如果suff[m-1-f+i]=i-q, suff[i]和suff[m-1-f+i]就没有直接关系了。

 

 

#include <stdio.h>

#define ASIZE 26
#define XSIZE 6

//坏字符规则计算
void preBmBc(char *x, int m, int bmBc[]) {  
	int i;  
	for (i = 0; i < ASIZE; ++i)         
		bmBc[i] = m;  
	
	for (i = 0; i < m - 1; ++i)    
		bmBc[x[i]-'a'] = m - i - 1;    
} 
//stuff辅助数组计算   
void suffixes(char *x, int m, int *suff) 
{    
	int f, g, i;   
	f = 0;            //上次匹配成功的位置
	suff[m - 1] = m;   
	g = m - 1;        //上次匹配失败的位置
	for (i = m - 2; i >= 0; --i) {  
		
		if (i > g && suff[i + m - 1 - f] < i - g)  
			
			suff[i] = suff[i + m - 1 - f];    
		else {  
			
			if (i < g)  
				
				g = i;  
			
			f = i;  
			
			while (g >= 0 && x[g] == x[g + m - 1 - f]) //匹配成功则一直匹配 
				
				--g;  
			
			suff[i] = f - g;  
			
		}  
		
	}  
	
}  
//好后缀规则实现
void preBmGs(char *x, int m, int bmGs[]) {  
	
	int i, j, suff[XSIZE];  
	
	suffixes(x, m, suff);    
	for (i = 0; i < m; ++i)  //情况3
        bmGs[i] = m;  
	
	j = 0;  
	
	for (i = m - 1; i >= 0; --i)   //情况2 
		
		if (suff[i] == i + 1)  
			
			for (; j < m - 1 - i; ++j)  
				
				if (bmGs[j] == m)  
					
					bmGs[j] = m - 1 - i;  
				
	for (i = 0; i <= m - 2; ++i)    //情况1  
					
		bmGs[m - 1 - suff[i]] = m - 1 - i;  
				
}  

int MAX(int a, int b)
{
	return a>b? a: b;
}

void print(int *t, int m)
{
	for (int i=0; i<m; i++)
	{
		printf("%d ", t[i]);
	}
	printf("\n");
}
//BM算法主体部分，x为模式串，y为目标串
void BM(char *x, int m, char *y, int n) {  
	
	int i, j, bmGs[XSIZE], bmBc[ASIZE];  
	
	/* Preprocessing */  
	  
	
	preBmBc(x, m, bmBc);  
	print(bmBc, ASIZE);

	preBmGs(x, m, bmGs);
	print(bmGs, XSIZE);
	
	/* Searching */  
	
	j = 0;  
	
	while (j <= n - m) {  
		
		for (i = m - 1; i >= 0 && x[i] == y[i + j]; --i);  
		
		if (i < 0) {  
			
			printf("%d ",j);
			
			j += bmGs[0];  
			
		}  
		
		else  
			
			j += MAX(bmGs[i], bmBc[y[i + j]-'a'] - m + 1 + i);  
		
	}   
}  

int main()
{
	char target[11] = "iabcdabcab";
	char pattern[XSIZE+1] = "dabcab";

	BM(pattern, XSIZE, target, 10);

	return 0;
}