监狱调整 POJ1636 Prison rearrangement 传递闭包FLoyd DFS 二维背包 动态规划DP

        第一遍读完题，可能没思路。试着从数据入手，看一下求解过程（以第三组数据为例）。如果第一个监狱选中1，也就是说要把1放到第二个监狱中，那么第二个监狱必须把1,2,3,4选中，因为它们不能和1在一起，否则就会发生冲突。同理，要把第二个监狱的1,2,3,4放到第一个监狱中，那么第一个监狱又要把与1,2,3,4冲突的都选出...... 

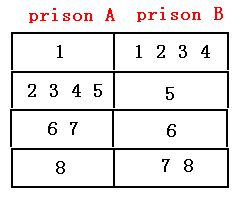
        这是个“牵一发而动全身”的过程。移动一个人的时候，可能会带动一大串同时移动。这样可以把监狱的人划分成好多组，每一组表示要同时移动的一串人。如下图，左边的代表监狱A，右边的代表监狱B。现在问题就变成这样了：两个监狱要以组为单位进行交换。因为最多交换一半，所以选第3、4组进行交换，最后每个监狱的交换人数为3。 

       从另一个角度，分组后的选择问题，有点像二维背包。每一组有两个值，从A里选的人数和从B里选的人数。即，每组相当于一个物品，有重量和体积。限制条件也有两个：从A中选择的总人数和从B中选择的总人数不能超过监狱容量的一半。即，背包的重量和体积都有限。最终要使交换的人尽可能的多。即，背包装得东西尽可能多。 

       哈哈，分析到这里，估计就有思路了。问题的求解可分为两个阶段：分组、二维背包。只要这两个部分解决了，问题就解决啦。 

     “万里长城第一步”------分组。如何分组？DFS or 传递闭包 都可以搞定。

(1) DFS，先A出发，沿冲突边到B，再从B出发沿冲突边到A，如此下去，直到走投无路。

(2)传递闭包，用Floyd。Floyd算法简单，实现无难度。关键是从Floyd的结果构造分组信息。这里不做解释，主要看代码。 

     “山穷水尽疑无路，柳暗花明又一村”------二维背包。背包问题很经典，要多练习。二维背包用的也是DP。

       状态转换方程：dp[k][i][j] = dp[k-1][i-a[k]][j-b[k]] || dp[k-1][i][j]。简单解释一下：dp[k][i][j]表示对前K组，用监狱A的i个人和监狱B的j个人交换是否成功。前K组的解与前K-1组有关。当前K-1组解决后，只要加上第K组就可以搞定前K组。对第K组有两种选择：选或不选。

不选第K组，则dp[K][i][j]能否成功取决于dp[k-1][i][j] 能否成功。

选第K组，则dp[K][i][j]能否成功取决于dp[k-1][i-a[k]][j-b[k]]能否成功。

  最后，两种情况只要有一种成功， dp[k][i][j] 就能成功。 好啦，已经说的太多了，具体看代码吧。

 代码（1）： DSF +　背包

#include <iostream>
using namespace std;

//***********************常量定义*****************************

const int SIZE = 205;


//*********************自定义数据结构*************************




//********************题目描述中的变量************************

//监狱的人数
int m;
//会发生冲突的对数
int r;


//**********************算法中的变量**************************

//map[i][j]表示i和j是否会冲突
int map[SIZE][SIZE];

//A组里的人数
int aSize;
//b组里的人数
int bSize;
//dp[i][j] 表示用A组的i个人换B组的j个人是否可行
bool dp[SIZE][SIZE];
//visited[0][i] 表示用A组中的点i是否被访问过
//visited[1][i] 表示用B组中的点i是否被访问过
bool visited[2][SIZE];


//***********************算法实现*****************************

void Init()
{
	memset( map, 0, sizeof(map) );
	memset( visited, 0, sizeof(visited) );
	memset( dp, 0, sizeof(dp) );
}

void Input()
{
	cin >> m >> r;
	for( int i=0; i<r; i++ )
	{
		int a, b;
		cin >> a >> b;
		map[a][b] = 1;
	}
}

//side=0  表示当前正在搜索A组
//side=1  表示当前正在搜索B组
//id 表示当前正在搜索的编号
void DFS( int side, int id )
{
	visited[side][id] = true;

	//如果当前搜索的是A组
	if( side == 0 )
	{
		//记录A组中的元素个数
		aSize++;
		for( int i=1; i<=m; i++ )
		{
			//搜索的是B组中对应的点
			if( map[id][i] && !visited[1][i] )
			{
				DFS( 1, i );
			}
		}
	}	
	else
	{
		bSize++;
		for( int j=1; j<=m; j++ )
		{			
			if( map[j][id] && !visited[0][j] )
			{
				DFS( 0, j );
			}
		}
	}
}

//利用二维背包计算
void Knapsack()
{
	dp[0][0] = true;
	for( int x=m/2; x>=aSize-1; x-- )
	{
		for( int y=m/2; y>=bSize-1; y-- )
		{
			//if( dp[x - aSize][y - bSize] )	dp[x][y] = true;
			if( dp[x][y] || dp[x - aSize][y - bSize] ) dp[x][y] = true;
		}
	}
}

void Output()
{
	for( int i=m/2; i>=0; i-- )
	{
		if( dp[i][i] )
		{
			cout << i << endl;
			break;
		}
	}
}

//************************main函数****************************

int main()
{
	freopen( "in.txt", "r", stdin );	
	
	int caseNum;
	cin >> caseNum;

	while( caseNum-- )
	{
		Init();		
		Input();
		for( int i=1; i<=m; i++ )
		{
			//跳过已经处理过的节点
			if( visited[0][i] ) continue;

			//计算A、B中的人数
			aSize = 0;
			bSize = 0;
			DFS( 0, i );	

			//利用二维背包计算
			Knapsack();
			
		}
		for( int i=1; i<=m; i++ )
		{			
			if( visited[1][i] ) continue;			
			aSize = 0;
			bSize = 0;
			DFS( 1, i );
			Knapsack();
			
		}
		Output();
	}
	return 0;
}

代码（２），传递闭包　＋　ＤＦＳ

#include <iostream>
using namespace std;

//***********************常量定义*****************************

const int SIZE = 410;


//*********************自定义数据结构*************************




//********************题目描述中的变量************************

//监狱的人数
int m;
//会发生冲突的对数
int r;


//**********************算法中的变量**************************

//map[i][j]表示i和j是否会冲突
int map[SIZE][SIZE];

int cnt;
int visited[SIZE];
int groupA[SIZE/2];
int groupB[SIZE/2];
int dp[SIZE/2][SIZE/2];

//***********************算法实现*****************************

void Input()
{
	//输入数据
	cin >> m >> r;

	//初始化map数组
	memset( map, 0, sizeof(map) );
	for( int j=1; j<=2*m; j++ )
	{
		map[j][j] = 1;
	}
	
	for( int i=0; i<r; i++ )
	{
		int a, b;
		cin >> a >> b;
		map[a][m+b] = 1;
		map[m+b][a] = 1;
	}
}

//求传递闭包
void Floyd()
{
	for( int i=1; i<=2*m; i++)
	{
		for( int j=1; j<=2*m; j++ )
		{
			if( map[i][j] == 1 )			
			{
				for( int k=1; k<=2*m; k++ )
				{
					//if( map[j][k] == 1 ) map[i][k] = 1;	
					map[i][k] = map[i][k] || ( map[i][j] && map[j][k] );
				}
			}
		}
	}
}

//填充数组 groupA[], groupB[] 
void Build()
{
	memset( visited, 0, sizeof(visited) );
	memset( groupA, 0, sizeof(groupA) );
	memset( groupB, 0, sizeof(groupB) );
	cnt = 0;

	for( int i=1; i<=2*m; i++ )
	{
		//跳过已访问的点
		if( visited[i] == 0 )
		{
			cnt++;

			for( int j=1; j<=2*m; j++ )
			{
				if( map[i][j] == 1 )
				{
					if( j<=m ) 
						groupA[cnt]++;
					else 
						groupB[cnt]++;

					visited[i] = 1; 
				}
			}
		}
	}
}

void Knapsack()
{
	memset( dp, 0, sizeof(dp) );
	dp[0][0] = 1;
	
	//二维背包问题
	for( int i=1; i<=cnt; i++ )
	{
		for( int j=m/2; j>=groupA[i]; j-- )
		{
			for( int k=m/2; k>=groupB[i]; k-- )
			{
				//dp[j][k] = dp[j][k] || dp[j - groupA[i]][k - groupB[i]];
				if( dp[j - groupA[i]][k - groupB[i]] )
				{
					dp[j][k] = 1;
				}
			}
		}
	}

	for( int i=m/2; i>=0; i-- )
	{
		if( dp[i][i] == 1 ) 
		{
			cout << i << endl;
			break;
		}
	}
}

//************************main函数****************************

int main()
{
	freopen( "in.txt", "r", stdin );	
	
	int caseNum;
	cin >> caseNum;

	while( caseNum-- )
	{
		Input();
		Floyd();
		Build();
		Knapsack();		
	}
	return 0;
}

 注：代码１已ＡＣ，代码２sample数据可过，提交ＷＡ，但思路应该没问题。哎，懒的调了。