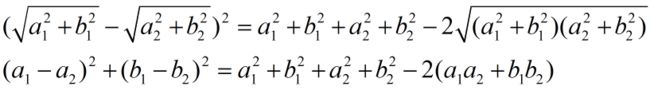spark-mllib-kmeans向量表示和距离计算
mllib在实现kmeans的过程中，对于距离的计算，使用了一些技巧。
首先要注意的是，mllib的jar中包org.apache.spark.mllib.linalg下定义了DenseVector，SparseVector，Vector等类或对象或特质。但实际上在真正计算过程中，mllib都是使用的breeze.linalg中的DenseVector，SparseVector，Vector等，mllib做了一个类似适配器的东西。所以名称不产生混乱，在import
breeze.linalg时都对相应的名称进行了重命名，比如Vectors.scala中的import breeze.linalg.{DenseVector => BDV, SparseVector => BSV, Vector => BV}，KMeans.scala中的import breeze.linalg.{DenseVector => BDV, Vector => BV, norm => breezeNorm}。
将
org.apache.spark.mllib.linalg下的Vector转化为BV就是使用一个方法toBreeze。
在进行kmeans运行之前，会先给每一个向量数据计算一个norms，如果向量是(a, b)，则norms就是
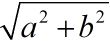。计算出norms后再与原向量做一个匹配zip，最后new出一个
BreezeVectorWithNorm对象，这是一个包含
BreezeVector和该向量的norm的一个对象。
。计算出norms后再与原向量做一个匹配zip，最后new出一个
BreezeVectorWithNorm对象，这是一个包含
BreezeVector和该向量的norm的一个对象。
def run(data: RDD[Vector]): KMeansModel = {
// Compute squared norms and cache them.
val norms = data.map(v => breezeNorm(v.toBreeze, 2.0))
norms.persist()
val breezeData = data.map(_.toBreeze).zip(norms).map { case (v, norm) =>
new BreezeVectorWithNorm(v, norm)
}
val model = runBreeze(breezeData)
norms.unpersist()
model
}
在做kmeans迭代和预测时，都要调用Kmeans.scala中的findClosest方法，该方法就是找到点与所有聚类中心最近的一个中心，这是一个相对比较大的计算，怎样减少计算量，此时norm就发挥作用了。先贴出源码：
private[mllib] def findClosest(
centers: TraversableOnce[BreezeVectorWithNorm],
point: BreezeVectorWithNorm): (Int, Double) = {
var bestDistance = Double.PositiveInfinity
var bestIndex = 0
var i = 0
centers.foreach { center =>
// Since `\|a - b\| \geq |\|a\| - \|b\||`, we can use this lower bound to avoid unnecessary
// distance computation.
var lowerBoundOfSqDist = center.norm - point.norm
lowerBoundOfSqDist = lowerBoundOfSqDist * lowerBoundOfSqDist
if (lowerBoundOfSqDist < bestDistance) {
val distance: Double = fastSquaredDistance(center, point)
if (distance < bestDistance) {
bestDistance = distance
bestIndex = i
}
}
i += 1
}
(bestIndex, bestDistance)
}
以下两条语句
var lowerBoundOfSqDist = center.norm - point.norm
lowerBoundOfSqDist = lowerBoundOfSqDist * lowerBoundOfSqDist
得到的
lowerBoundOfSqDist是一个怎样的东西呢？如果中心点center是(a1,b1)，需要计算的点
point
是(a2,b2)。那么
lowerBoundOfSqDist是：
如下是展开式，第二个是真正计算欧式距离时的除去开平方的公式。（在查找最短距离的时候无需计算开方，因为只需要计算出开方里面的式子就可以进行比较了，mllib也是这样做的）
可轻易证明上面两式的第一式将会小于等于第二式，因此在进行距离比较的时候，先计算很容易计算的
lowerBoundOfSqDist，如果
lowerBoundOfSqDist都不小于之前计算得到的最小距离
bestDistance，那真正的欧式距离也不可能小于
bestDistance了，因此这种情况下就不需要去计算欧式距离，省去很多计算工作。如果
lowerBoundOfSqDist小于了
bestDistance，则进行距离的计算，调用
fastSquaredDistance，这个方法将调用MLUtils.scala里面的fastSquaredDistance方法。贴源码：
private[mllib] def fastSquaredDistance(
v1: BV[Double],
norm1: Double,
v2: BV[Double],
norm2: Double,
precision: Double = 1e-6): Double = {
val n = v1.size
require(v2.size == n)
require(norm1 >= 0.0 && norm2 >= 0.0)
val sumSquaredNorm = norm1 * norm1 + norm2 * norm2
val normDiff = norm1 - norm2
var sqDist = 0.0
/*
* The relative error is
* <pre>
* EPSILON * ( \|a\|_2^2 + \|b\\_2^2 + 2 |a^T b|) / ( \|a - b\|_2^2 ),
* </pre>
* which is bounded by
* <pre>
* 2.0 * EPSILON * ( \|a\|_2^2 + \|b\|_2^2 ) / ( (\|a\|_2 - \|b\|_2)^2 ).
* </pre>
* The bound doesn't need the inner product, so we can use it as a sufficient condition to
* check quickly whether the inner product approach is accurate.
*/
val precisionBound1 = 2.0 * EPSILON * sumSquaredNorm / (normDiff * normDiff + EPSILON)
if (precisionBound1 < precision) {
sqDist = sumSquaredNorm - 2.0 * v1.dot(v2)
} else if (v1.isInstanceOf[BSV[Double]] || v2.isInstanceOf[BSV[Double]]) {
val dot = v1.dot(v2)
sqDist = math.max(sumSquaredNorm - 2.0 * dot, 0.0)
val precisionBound2 = EPSILON * (sumSquaredNorm + 2.0 * math.abs(dot)) / (sqDist + EPSILON)
if (precisionBound2 > precision) {
sqDist = breezeSquaredDistance(v1, v2)
}
} else {
sqDist = breezeSquaredDistance(v1, v2)
}
sqDist
}
该方法会先计算一个精度，
有关精度的计算
val precisionBound1 = 2.0 * EPSILON * sumSquaredNorm / (normDiff * normDiff + EPSILON)目前我还搞不懂，如果在精度满足条件的情况下，则使用计算出的norms在减去2倍向量内积值就可得到欧式距离的平方值了，即
sqDist = sumSquaredNorm - 2.0 * v1.dot(v2)，
sumSquaredNorm即为
，
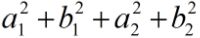2.0 * v1.dot(v2)即为
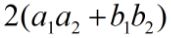。这也是之前将norm计算出来的好处。如果精度不满足要求，则进行实实在在的原始的距离计算公式了
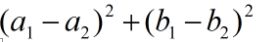，即调用
breezeSquaredDistance，该方法的代码为：
，
2.0 * v1.dot(v2)即为
。这也是之前将norm计算出来的好处。如果精度不满足要求，则进行实实在在的原始的距离计算公式了
，即调用
breezeSquaredDistance，该方法的代码为：
implicit def squaredDistanceFromZippedValues[T, U](implicit zipImpl: zipValues.Impl2[T, U, ZippedValues[Double, Double]]): Impl2[T, U, Double] = {
new Impl2[T, U, Double] {
def apply(v: T, v2: U): Double = {
var squaredDistance = 0.0
zipValues(v, v2).foreach { (a, b) =>
val score = a - b
squaredDistance += (score * score)
}
squaredDistance
}
}
}
一板一眼，很清楚。