C++矩阵处理库(比LAPACK更方便)——Eigen详细解析
前言:
这段时间总算是把开题答辩的事情搞完了,心情总算是放松了一点,今天先总结总结这几天一直在使用的矩阵处理库。相信大家在做Matlab项目的时候,如果想移植为C++总是犯头疼,没有一个好的线性代数库可以使用,有些别人自己写的矩阵库却又不支持复数,或者是缺少算点积,解线性方程组的功能。今天给大家介绍的这个库可以完全解决这些问题,甚至还提供了许多Matlab才有的矩阵处理方式,十分的方便。
安装:
下载地址:
http://eigen.tuxfamily.org/index.php?title=Main_Page#Download
点进去如图
现在最新的版本就是如图右上角的3.2.5版本,下载下来之后
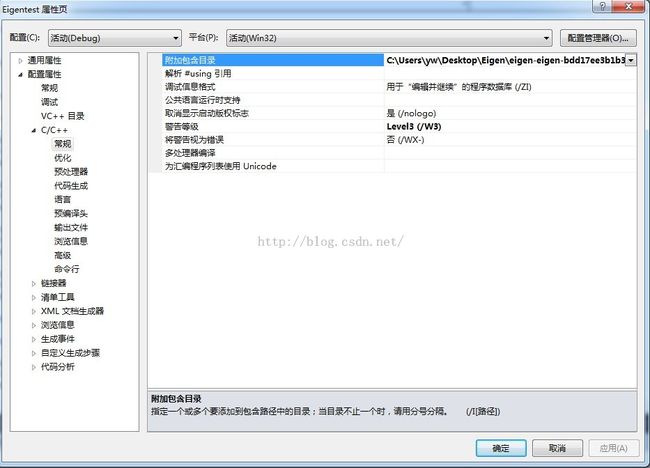
解压,然后把解压包的路径加入工程中就可以编译使用了。我用的是vs2010,加入方式是右击解决方案点击属性:
配置属性 -> C/C++ ->常规 中的附加包含目标,把解压地址贴上就行(解决方案里需要有cpp文件才会有这个选项)
这个是我的地址,C:\Users\yw\Desktop\Eigen\eigen-eigen-bdd17ee3b1b3 如下图
添加成功后就可以使用了。
使用方法:
头文件:
只用包含
#include <Eigen/Eigen>
就包含了Eigen库所有的头文件了,如果不需要全部包含,可以自行查看下载下来的EIgen文件夹下的头文件,里面有所有的包含关系。
定义矩阵/支持的数据类型
int main(int, char *[])
{
<span style="white-space:pre"> </span>Matrix3f m3;
<span style="white-space:pre"> </span>m3 << 1, 2, 3, 4, 5, 6, 7, 8, 9;
<span style="white-space:pre"> </span>Matrix4f m4 = Matrix4f::Identity();
<span style="white-space:pre"> </span>Vector4i v4(1, 2, 3, 4);
<span style="white-space:pre"> </span>std::cout << "m3\n" << m3 << "\nm4:\n"
<span style="white-space:pre"> </span><< m4 << "\nv4:\n" << v4 << std::endl;
}
/*
output: m3 1 2 3 4 5 6 7 8 9 m4: 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 v4: 1 2 3 4
*/
Vector代表向量,其中的4代表是4×1的向量,最后的i代表是int数据格式,同理f代表float,d代表double,
其中例子没列出的,cd代表最棒的
std::complex<double>加上c就变成了complex模板库数据格式。
Matrix代表矩阵,3,4代表为定义的3×3,4×4矩阵,f代表float。
这里使用的是预先定义了大小的矩阵和向量。Eigen库中既有矩阵,也有向量,1×N 或者N×1 的矩阵的形式与向量相同,因此Eigen库在需要向量的时候,提供1×N 或者N×1 的矩阵同样可以运行,所以如果不是特别需求,可以只使用矩阵。
动态生成的矩阵:
MatrixXd m(2,2);
//method 1
m(0,0) = 3;
m(1,0) = 2.5;
m(0,1) = -1;
m(1,1) = m(1,0) + m(0,1);
其中 MatirxXd, Matrix是矩阵,X代表动态生成,d代表double。声明的时候可以声明大小也可以不声明,如上例子是。
MatrixXf m(2,2);声明一个大小为2 ×2的矩阵m。访问方式就是括号中下标,不过计数从0开始,需要小心。
MatrixXf m3;
m3=m1*m2;
这是不声明大小的动态矩阵,由矩阵m1和m2的乘法决定。
这是最基础的矩阵数据类型与矩阵大小定义。
初始化矩阵
三种方式:
//method 1
m(0,0) = 3;
m(1,0) = 2.5;
m(0,1) = -1;
m(1,1) = m(1,0) + m(0,1);
//method 2
m<<3,-1,
2.5,-1.5;
cout <<"m=\n"<< m << endl; 这里是最基础的2种初始化方式,可以第一种在循环中可以很好的幅值。
获取行列数/获取一行或者一列
int row, column;
<span style="font-size: 13.3333339691162px; white-space: pre;"> </span><span style="font-size: 13.3333339691162px;">mat1.row(i) = mat2.col(j);</span><br style="font-size: 13.3333339691162px;" /><span style="font-size: 13.3333339691162px; white-space: pre;"> </span><span style="font-size: 13.3333339691162px;">mat1.col(j1).swap(mat1.col(j2));</span>
</pre><pre name="code" class="cpp">rows()与cols()函数获取行列数,row()与col()获取矩阵的一行,或者一列。在提取向量时非常好用,
类Matlab的块状赋值
<span style="white-space:pre"> </span>Matrix4i m = Matrix4i::Random(); <span style="white-space:pre"> </span>cout << "Here is the matrix m:" << endl << m << endl; <span style="white-space:pre"> </span>cout << "Here is the bottom-right 2x3 corner in m:" << endl <span style="white-space:pre"> </span><< m.corner(Eigen::BottomRight, 2, 3) << endl; <span style="white-space:pre"> </span>m.corner(Eigen::BottomRight, 2, 3).setZero(); <span style="white-space:pre"> </span>cout << "Now the matrix m is:" << endl << m << endl;
/* Output 7 9 -5 -3 -2 -6 1 0 6 -3 0 9 6 6 3 9 Here is the bottom-right 2x3 corner in m: -3 0 9 6 3 9 Now the matrix m is: 7 9 -5 -3 -2 -6 1 0 6 0 0 0 6 0 0 0
/*
如上例子所示
mat1.corner(TopLeft,rows,cols) mat1.corner(TopRight,rows,cols) mat1.corner(BottomLeft,rows,cols) mat1.corner(BottomRight,rows,cols)使用corner函数可以得到一个矩阵中的一部分,第一个参数描述其在原矩阵中的方位,后面两个参数描述大小。
求余子式
有了这个就可以非常方便的求一个矩阵中划去第num行,第num列的余子式。代码如下:
MatrixXcd m4(row-1,row-1);
if(num ==1)
{
m4 = m3.corner(Eigen::BottomRight, row-1, row-1);
}
else if(num == row)
{
m4 = m3.corner(Eigen::TopLeft, row-1, row-1);
}
else
{
m4<<m3.corner(Eigen::TopLeft, num -1, num-1),
m3.corner(Eigen::TopRight, num-1, row -num),
m3.corner(Eigen::BottomLeft, row -num, num -1),
m3.corner(Eigen::BottomRight, row -num, row -num); }其中m4是新生成的余子式矩阵,m3是原矩阵,row和column参数是原矩阵的行列数。
点积,向量积
| dot product (inner product) |
scalar = vec1.dot(vec2);
|
| cross product |
#include <Eigen/Geometry>
vec3 = vec1.cross(vec2);
|
转置,伴随矩阵
| transposition (read-write) |
mat3 = mat1.transpose() * mat2;
mat3.transpose() = mat1 * mat2.transpose();
|
| adjoint (read only) |
mat3 = mat1.adjoint() * mat2;
|
求解线性方程组:
支持的种类
LU/Cholesky/QR
这里我只给出最通用的解法LU的使用方式(其官网上的例子有误,需要查找自带的example工程)
VectorXcd x; x = m4.lu().solve(b);
求解形如
AX=b
的方程,其中m4则为上式的A,b可为矩阵也可以为向量,只要满足b的行数等于A的行数。
自学网站:
新手入门:
http://eigen.tuxfamily.org/dox-2.0/TutorialCore.html
http://eigen.tuxfamily.org/dox-2.0/TutorialCore.html
http://eigen.tuxfamily.org/dox-2.0/TutorialAdvancedLinearAlgebra.html
第一个地址是核心部分,包括了赋值,加减乘除的基础操作。
第二个是图像处理相关的。
第三个为求解线性方程组的部分,以及矩阵分解。
建议大家读英文的说明,不要翻译成中文阅读。不然容易由于翻译问题误解
论坛
https://forum.kde.org/viewforum.php?f=74
相关博客
http://blog.csdn.net/abcjennifer/article/details/7781936
最初就是看了这位浙大姐姐的博客安装上了Eigen,然后自己看英文文档学习怎么使用。