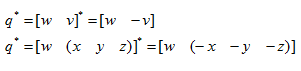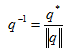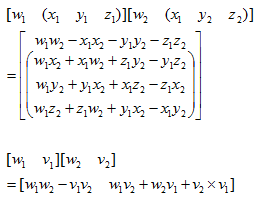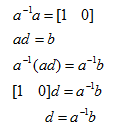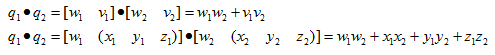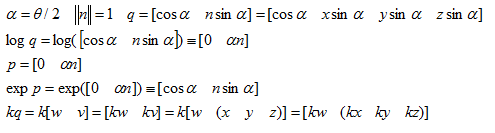3D数学读书笔记——四元数
本系列文章由birdlove1987编写,转载请注明出处。
文章链接: http://blog.csdn.net/zhurui_idea/article/details/25400659
什么是四元数
复数是由实数加上虚数单位 i 组成,其中
i² = -1
相似地,四元数都是由实数加上三个元素 i、j、k 组成,而且它们有如下的关系:
i² = j² = k² = ijk = -1
每个四元数都是 1、i、j 和 k 的线性组合,即是四元数一般可表示为a + bi + cj + dk。
关于四元数的历史
四元数是由哈密顿在1843年爱尔兰发现的。当时他正研究扩展复数到更高的维次(复数可视为平面上的点)。他不能做到三维空间的例子,但四维则造出四元数。根据哈密顿记述,他于10月16日跟他的妻子在都柏林的皇家运河(Royal Canal)上散步时突然想到
i² = j² = k² = ijk = -1
的方程解。之后哈密顿立刻将此方程刻在附近布鲁穆桥(Brougham Bridge,现称为金雀花桥 Broom Bridge)。
不只如此,哈密顿还创造了向量的内外积(大神就是大神,创造力旺盛啊-_-!)。他亦把四元数描绘成一个有序的四重实数:一个标量(a)和向量(bi + cj + dk)的组合。若两个标量部为零的四元数相乘,所得的标量部便是原来的两个向量部的标量积的负值,而向量部则为向量积的值,但它们的重要性仍有待发掘。
四元数的记法
一个四元数包含一个标量分量和一个3D向量分量。经常记标量分量为w,记向量分量为单一的v或分开的x,y,z。两种记法分别如下:
[w,v]
[w,(x,y,z)]
四元数的性质(当年计算机图形学考的就是这题。。呜呜呜~~)
四元数不像实数或复数那样,它的乘法是不可交换的,例如
i j = k, , j i = -k ;
j k = i , k j = -i ;
k i = j , i k = -j .
四元数是除法环的一个例子。除了没有乘法的交换律外,除法环与域是相类的。特别地,乘法的结合律仍旧存在、非零元素仍有唯一的逆元素。
负四元数
四元数能求负。做法很直接:将每个分量都变负。
-q = - [ w ( x y z ) ] = [ -w ( -x -y -z ) ]
= - [ w v ] = [ -w -v ]
ps:q 和 - q代表的实际角位移是相同的,因此,3D中的任意角位移都有两中不同的四元数表示方法,它们互相为负。(因为绕某个轴旋转360°物体相当于没有旋转)
单位四元数
几何上,存在两个单位四元数,它们代表没有角位移:[ 1, 0 ] 和 [ -1, 0 ]
数学上,实际只有一个单位四元数 [ 1 , 0 ] 用任意四元数q乘以单位四元数,结果仍是q。数学上认为[ -1 , 0]不是正在的单位四元数。
四元数的模、共轭和逆
四元数的模的记法和求法公式:
四元数的共轭记作 q* ,可通过让四元数的向量部分变负来获得。
四元数的逆记作![]() ,定义为四元数的共轭除以它的模。
,定义为四元数的共轭除以它的模。
四元数的乘法(叉乘)
四元数叉乘满足结合律,但不满足交换律。
(ab)c=a(bc)
ab≠ba
四元数乘积的模等于模的积
||pq|| = ||p|| ||q||
四元数的“差”
四元数的“差”被定义为一个方位到另一个方位的角位移。换句话说,给定方位a和b,就能计算a旋转到b的角位移d。
四元数点乘
对于单位四元数a和b,有-1 ≤ a·b ≤ 1。通常我们只关心a·b的绝对值,因为a·b=-(a·-b),所以b和-b代表相同的角位移。
四元数点乘的几何解释类似于向量点乘的几何解释。四元数点乘a·b的绝对值越大,a和b代表的角位移越相似。
四元数的对数、指数和标量乘运算
四元数求幂
对四元数求幂在3D编程中非常有用,因为它可以从角位移中抽取一部分,例如四元数q代表一个角位移,现在想得到代表1/3这个角位移的四元数,可以计算q^1/3
四元数数幂的求法
在实际3D转换中我们使用这个的代码进行抽取角位移的部分
// 四元数(输入、输出)
float w,x,y,z;
// 指数(输入)
float zhishu;
// 为了避免除零,我们这里做一个判断,因为第一个变量时cos,所以这里是.9999f
if (fabs(w) < .9999f) {
// 提取半角alpha
float alpha = acos(w);
// 计算新的alpha
float newAlpha = alpha * exponent;
// 计算新的w值
w = cos(newAlpha);
// 计算新的xyz的值
float temp = sin(newAlpha) / sin(alpha);
x *= temp;
y *= temp;
z *= temp;
}
使用程序前应先进行单位四元数的检查,因为w=±1会导致temp的计算中出现除零的现象,如果检测出是单位四元数,直接返回原四元数即可。
四元数插值
当今3D数学中四元数存在的理由是由于一种叫做slerp的运算,它是球面线性插值的缩写(Spherical Linear Interpolation)。slerp运算非常有用,因为它可以在两个四元数间平滑插值。slerp运算避免了欧拉角插值的所有问题。
slerp是一种三元运算,这意味着它有三个操作数。前两个操作数是两个四元数,将在它们中间插值。设这两个开始和结束的四元数分别为q0和q1.差值参数设为变量 t,t 在0到1之间变化。slerp函数:slerp(q0,q1,t) 将返回q0和q1之间的插值方位。
// 两个输入四元数
float w0,x0,y0,z0;
float w1,x1,y1,z1;
// 差值变量
float t;
// 输出四元数
float w,x,y,z;
// 用点乘计算两个四元数夹角的cos值
float cosJiao = w0*w1 + x0*x1 + y0*y1 + z0*z1;
// 如果点乘为负,则反转一个四元数以取得短的4D弧
if (cosJiao < 0.0f) {
w1 = –w1;
x1 = –x1;
y1 = –y1;
z1 = –z1;
cosJiao = –cosJiao;
}
// 检查防止除零
float k0, k1;
if (cosJiao > 0.9999f) {
// 如果非常接近,就线性插值
k0 = 1.0f–t;
k1 = t;
} else {
// 利用三角公式sin²+cos²=1计算sin值
float sinJiao = sqrt(1.0f – cosJiao*cosJiao);
// 通过sin和cos计算角度
float Jiao = atan2(sinJiao, cosJiao);
// 计算分母的倒数从而避免使用除法
float oneOverSinJiao = 1.0f / sinJiao;
// 计算插值变量
k0 = sin((1.0f – t) * Jiao) * oneOverSinJiao;
k1 = sin(t * Jiao) * oneOverSinJiao;
}
// 插入值
w = w0*k0 + w1*k1;
x = x0*k0 + x1*k1;
y = y0*k0 + y1*k1;
z = z0*k0 + z1*k1;
嘿嘿,四元数这个地方确实有点难度。。不过3D整体都不太简单,所有好好加油!
—End—
参考文献: (1)《3D Math Primer for Graphics and Game Development》
(2) 维基百科
(3) 《计算机图形学》