字典树 Trie 的实现
Trie树,又称为字典树,是一种树形结构,是一种哈希树的变种,是一种用于快速检索的多叉树数据结构。
用于保存大量的字符串。它的优点是:利用字符串的公共前缀来节约存储空间。
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
它有3个基本性质:
1、根节点不包含字符,除根节点外每一个节点都只包含一个字符。
2、从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
3、每个节点的所有子节点包含的字符都不相同。
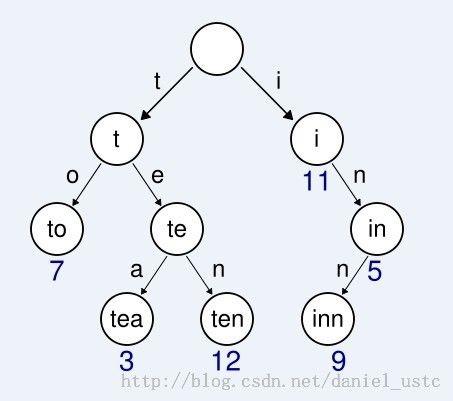
这是一个Trie结构的例子:
在这个Trie结构中,保存了t、to、te、tea、ten、i、in、inn这8个字符串,仅占用8个字节(不包括指针占用的空间)。
搭建Trie的基本算法很简单,无非是逐一把每则单词的每个字母插入Trie。插入前先看前缀是否存在。如果存在,就共享,否则创建对应的节点和边。
比如要插入单词int,就有下面几步:
1.考察前缀"i",发现边i已经存在。于是顺着边i走到节点i。
2.考察剩下的字符串"nt"的前缀"i",发现从节点i出发,已经有边n存在。于是顺着边n走到节点in
3.考察最后一个字符"t",这下从节点in出发没有边t了,于是创建节点in的子节点int,并把边in->int标记为t。
(这个图示比较形象)
用途:
典型应用是用于统计和排序、查询大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本的词频统计等。
具体Trie树的创建、插入、查询代码如下所示:
/*
功能描述:实现trie树的创建、插入、查询
说明:
对统计对象,要求符合正则"[a-z]*"的格式的单词
若考虑大写,标点和空白字符(空格.TAB.回车换行符),
可修改next数组大小,最多255可包含所有字符
*/
#include<stdio.h>
#include <stdlib.h>
#include<string.h>
#define MAX_CHILD 26 //此函数只考虑26个英文字母的情况
typedef struct Tree
{
int count; //用来标记该节点是个可以形成一个单词,如果count!=0,则从根节点到该节点的路径可以形成一个单词
struct Tree *child[MAX_CHILD];
} Node,*Trie_node;
/*
child是表示每层有多少种类的数,如果只是小写字母,则26即可,若改为大小写字母,则是52,若再加上数字,
则是62了,这里根据题意来确定。
count可以表示一个字典树到此有多少相同前缀的数目,这里根据需要应当学会自由变化。
*/
Node* CreateTrie() //创建trie节点树
{
Node *node=(Node*)malloc(sizeof(Node));
memset(node,0,sizeof(Node));
return node;
}
void insert_node(Trie_node root,char *str) //trie树插入结点
{
if(root ==NULL || *str=='\0')
return;
Node *t=root;
while(*str!='\0')
{
if(t->child[*str-'a']==NULL)
{
Node *tmp=CreateTrie();
t->child[*str-'a']=tmp;
}
t=t->child[*str-'a'];
str++;
}
t->count++;
}
void search_str(Trie_node root,char *str) //查找串是否在该trie树中
{
if(NULL==root || *str=='\0')
{
printf("trie is empty or str is null\n");
return;
}
Node *t=root;
while(*str!='\0')
{
if(t->child[*str-'a']!=NULL)
{
t=t->child[*str-'a'];
str++;
}
else
break;
}
if(*str=='\0')
{
if(t->count==0)
printf("该字符串不在trie树中,但该串是某个单词的前缀\n");
else
printf("该字符串在该trie树中\n");
}
else
printf("该字符串不在trie树中\n");
}
void del(Trie_node root) //释放整个字典树占的堆空间
{
int i;
for(i=0; i<MAX_CHILD; i++)
{
if(root->child[i]!=NULL)
del(root->child[i]);
}
free(root);
}
int main()
{
int i,n;
char str[20];
printf("请输入要创建的trie树的大小:");
scanf("%d", &n);
Trie_node root=NULL;
root=CreateTrie();
if(root==NULL)
printf("创建trie树失败\n");
for(i=0; i<n; i++)
{
scanf("%s",str);
insert_node(root,str);
}
printf("trie树已建立完成\n");
printf("请输入要查询的字符串:\n");
while(scanf("%s",str)!=NULL)
{
search_str(root,str);
}
return 0;
}
Python内置的dict是用哈希实现的,正好可以解决这两个问题。(dict的基本原理可以参考《Python源码剖析》阅读笔记:第五章-dict对象)
- dict采用的是开放寻址法解决冲突,节省了内存,但时间复杂度还是O(1)。
- dict这个哈希表里可以放任意字符作为键,中文当然也不例外。
Python版的关键改造就是节点的next表用dict代替,维护的是字符->子节点的映射。查找时,若待查询字符是next里的一个键就说明该字符在Trie树里,以这个键得到值就能找到下一节点。插入时也只要插入字符->子节点的映射就可以了。
#!/usr/bin/env python3
class Trie:
root = dict()
def insert(self, string):
index, node = self.findLastNode(string)
for char in string[index:]:
new_node = dict()
node[char] = new_node
node = new_node
def find(self, string):
index, node = self.findLastNode(string)
return (index == len(string))
def findLastNode(self, string):
'''
@param string: string to be searched
@return: (index, node).
index: int. first char(string[index]) of string not found in Trie tree. Otherwise, the length of string
node: dict. node doesn't have string[index].
'''
node = self.root
index = 0
while index < len(string):
char = string[index]
if char in node:
node = node[char]
else:
break
index += 1
return (index, node)
def printTree(self, node, layer):
if len(node) == 0:
return '\n'
rtns = []
items = sorted(node.items(), key=lambda x:x[0])
rtns.append(items[0][0])
rtns.append(self.printTree(items[0][1], layer+1))
for item in items[1:]:
rtns.append('.' * layer)
rtns.append(item[0])
rtns.append(self.printTree(item[1], layer+1))
return ''.join(rtns)
def __str__(self):
return self.printTree(self.root, 0)
if __name__ == '__main__':
tree = Trie()
while True:
src = input()
if src == '':
break
else:
tree.insert(src)
print(tree)