UVa OJ 121 - Pipe Fitters (装管子)
Time limit: 3.000 seconds
限时:3.000秒
Background
背景
Filters, or programs that pass "processed" data through in some changed form, are an important class of programs in the UNIX operating system. A pipe is an operating system concept that permits data to "flow" between processes (and allows filters to be chained together easily.)
在UNIX操作系统中,过滤器是重要的一类程序。通过它“处理”的数据,其格式会发生改变。管道是操作系统中的一个概念,它使得数据可以在进程间流动(也很容易和过滤器相连,协同工作)。
This problem involves maximizing the number of pipes that can be fit into a storage container (but it's a pipe fitting problem, not a bin packing problem).
这个问题是关于使装入贮藏箱的管子数量最大化(这是关于管子贮藏的问题,不是装箱问题)。
The Problem
问题
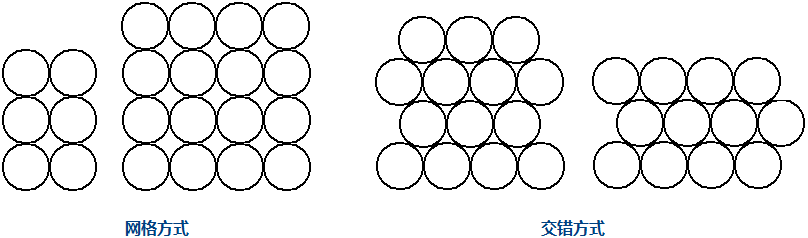
A company manufactures pipes of uniform diameter. All pipes are stored in rectangular storage containers, but the containers come in several different sizes. Pipes are stored in rows within a container so that there is no space between pipes in any row (there may be some space at the end of a row), i.e., all pipes in a row are tangent, or touch. Within a rectangular cross-section, pipes are stored in either a grid pattern or a skew pattern as shown below: the two left-most cross-sections are in a grid pattern, the two right-most cross-sections are in a skew pattern.
一家公司生产一种直径相同的管子。所有管子都存储在矩形贮藏箱中,但贮藏箱的尺寸大小不一。管子按行排列在一个贮藏箱内,以使每行管子之间没有任何的空隙(在一行的两端可能存在空隙),也就是说所有放在同一行的管子都是相切的,或说是外接的。下图显示了一个贮藏箱的矩形横截面,可以看到管子只按“网格”和“交错”两种方式装入:左边的两组横截面是“网格”方式,右边的两组横截面是“交错”方式。
Note that although it may not be apparent from the diagram, there is no space between adjacent pipes in any row. The pipes in any row are tangent to (touch) the pipes in the row below (or rest on the bottom of the container). When pipes are packed into a container, there may be "left-over" space in which a pipe cannot be packed. Such left-over space is packed with padding so that the pipes cannot settle during shipping.
注意,任何一行相邻的管子间都没有间隔,这可能在图中看不清楚。每行管子都与下一行管子相切(外接),最底下一行与贮藏箱底相切。当管子装入贮藏箱后,可能会留下一些不够放进一个管子的空间。因此需要将这些空间填充满,否则船运将无法启程。
The Input
输入
The input is a sequence of cross-section dimensions of storage containers. Each cross-section is given as two real values on one line separated by white space. The dimensions are expressed in units of pipe diameters. All dimensions will be less than 27. Note that a cross section with dimensions a×b can also be viewed as a cross section with dimensions b×a.
输入是一组 贮藏箱横截面的尺寸。每个横截面数据独占一行,给出两个实数值,中间以空格隔开。尺寸的单位就是 一个管子的直径。所有尺寸都小于27。注意,尺寸为a×b的横截面,也可看做是b×a的。
The Output
输出
For each cross-section in the input, your program should print the maximum number of pipes that can be packed into that cross section. The number of pipes is an integer -- no fractional pipes can be packed. The maximum number is followed by the word "grid" if a grid pattern results in the maximal number of pipes or the word "skew" if a skew pattern results in the maximal number of pipes. If the pattern doesn't matter, that is the same number of pipes can be packed with either a grid or skew pattern, then the word "grid" should be printed.
对应于每一行横截面的输入,你的程序要打印出在这个横截面中能装入管子的最大数量。该数量由一个整数表示——不存在半个管子的情况。后面输出一个单词“grid”或着“skew”,分别表示达到最大数量的装法是网格或交错。如果两种装法都能够达到相同的最大数量,则输出“grid”。
Sample Input
输入示例
3 3
2.9 10
2.9 10.5
11 11
Sample Output
输出示例
9 grid
29 skew
30 skew
126 skew
Analysis
分析
这是很有意思的一道数学题。按题目要求每行管子之间不能有空隙,因此任意上下两个管子的位置关系只能有两种:正对或60度斜错,其它的角度都会使上一行或下一行的管子间产生空隙。题目还给出管子的直径是一个单位,这样问题就简单多了。那么如果是网格方式排列(即上下正对),那么直接将贮藏箱的长宽取整即为可容纳管子的数量。
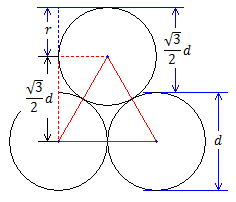
如果是交错排列(上下行斜错60度),情况稍有点复杂。为方便描述,我们把箱子最底一的一行称为第0行,之上一行为第1行,以此类推。第0行的行高显然为直径,从第1行开始向上,每行的行高都为下面一行的顶到这一行顶的距离。该行高可简单的用勾股定理计算,方法见下图:
图中r为半径,d为直径,红色等边三角形的顶点分别为三个管子横截面的圆心。可以看出,上面一行的行高即等于该三角形的高,由此可计算出贮藏箱一共可以放多少行。但列的情况又稍有不同,如下图所示:
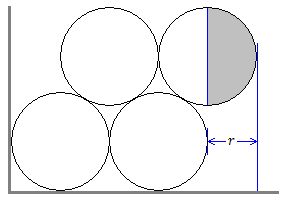
如果最底一行在放满管子后,剩下的空间大于半径,那么上面的所有行都可放置相同数量的管子。但如果剩下的空间不足半径,那么奇数行就只能放下的数量就比偶数行少1个。为方便计算,可先按每行相同数量的管子乘以行数,得到所有的管子数量,然后减掉不能放下的奇数行的管子。具体实现方法详见下面代码中的注释。
Solution
解答
#include <iostream>
using namespace std;
//计算交错排列法的数量
int Skew(float x, float y) {
//fSqrt3_2为开方3除以2,表示相邻两行顶部间的距离
static const float fSqrt3_2 = 0.8660254f;
//计算可以排下的总行数。除最底行高为1,其余行高为fSqrt3_2
int nRows = (y >= 1) + (int)((y - 1) / fSqrt3_2);
//先计算出最底一行排满的列数,如果最底行剩下的空间不足0.5
//则说明奇数行(底行为0)的列数比偶数行少1个,要对奇数行每行减1
return (nRows * (int)x - (nRows / 2) * (x - (int)x < 0.5f));
}
//主函数
int main(void) {
//循环读入并处理所有数据
for (float x, y; cin >> x >> y; cout << endl) {
//网格方式排列,即为简单的行列取整。交错方式要计算两个方向
int nGrid = (int)x * (int)y, nSkew = max(Skew(x, y), Skew(y, x));
//输出最大的管子数及其排列方式
cout << max(nGrid, nSkew) << (nGrid >= nSkew ? " grid" : " skew");
}
return 0;
}