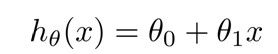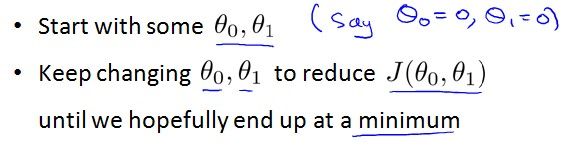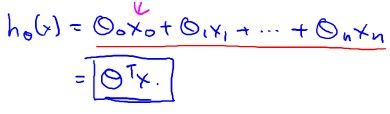Standford 机器学习学习笔记 线性回归（Linear Regission）

        本节内容主要包含单变量（One Variable）和求解costfunction的最优值的学习算法—梯度下降法（Gradientdescent）以及多变量（multipleVariable）的线性回归。

1.      单变量的线性回归（Linear Regission with onevariable）

        监督学习的样本中都含有对于每个输入变量的输出值，通过建立模型并且学习得到一个模型之后，使该模型可以通过给定的输入，预测出输出。

 

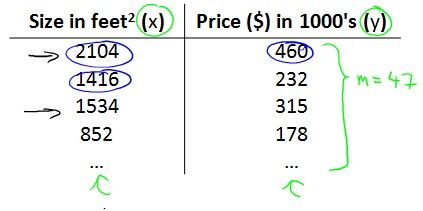
        现在有这样的一组样本数据，我们需要通过该样本输入学习模型预测给定面积的房子的价格，建立模型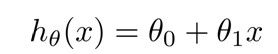：Notation：m是样本个数，x是面积，y是价格

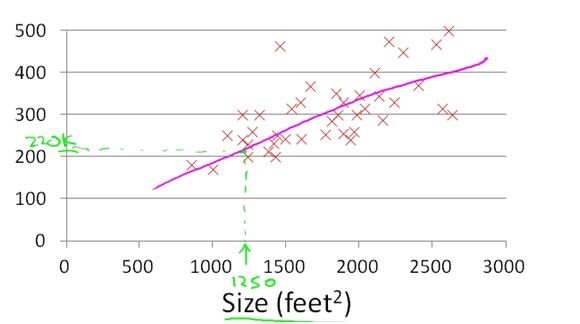
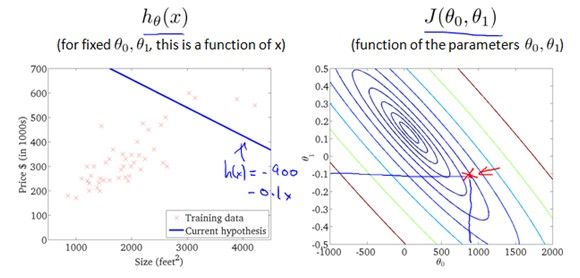
样本分布如下：

 

        现在要学习出一个最适合该样本数据的模型，让训练出的模型最接近样本的输出y，自然而然会想到CostFunction为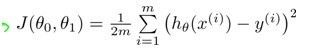，（至于为什么是它，请参考ttp://blog.csdn.net/usingnamespace_std/article/details/8883782），学习的目标是得到一个theta值使J最小

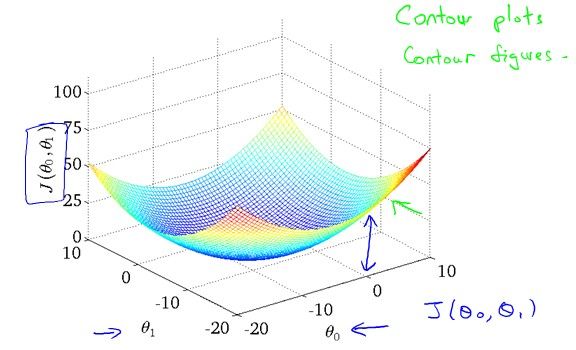
J(theta0,theta1)的图像是这样的

 

上面的每一个点对应于中的一个模型。

 

2.      梯度下降法（Gradient Descent）

        梯度下降法的原理是选取一个初始点，选取下降最快的方向向下走，直到走到极值点（即梯度为0的点）。

算法描述：

        由于函数可能存在多个极小值点，因此，梯度下降法得到的是局部最小值，而对于convex函数，局部最小值就是全局最小值，线性回归模型中的目标函数J就是convex函数，因此不用担心取不到最小值的问题。对于非convex函数，那么需要选取多个初始值进行梯度下降，选取最好的那个值。

 

        算法描述如下：

        这边注意每次迭代更新是同时更新（simultaneousupdate），即对j时求偏导时，用到的theta是旧的theta。

Alpha的选取：如果alpha选取得太大，会导致算法不会收敛，因为每次迭代后梯度都会变大，而离目标越来越远，如果在实践中发现算法未能收敛，那么有可能是alpha选的太大了。

 

        相反，如果alpha选取过小虽然对算法的收敛没有影响，但是会影响到算法的效率，它会导致算法过慢收敛。

Batch Gradient Decent：

        每次迭代需要计算所有样本的梯度之和，如果样本数量过大，算法的效率会很低。

Stochastic Gradient Decent：

        每次只用一个样本进行迭代，虽然每次迭代不一定是往梯度最大的方向走的，但是也会最终收敛到最优值。

 

 

        通过梯度下降法来求解J(theta)根据算法定义，可以推导出：

 

 

3.      多变量的线性回归（Linear regission withmultiple Variable）

        现实情况中，房价会受到面积以外的其他因素影响，比如房价数量，楼层数，房子的年龄等。

 

        每一个样本的feature可以用一个向量X来表示，如果有n个feature，那么X的维数是n+1维的，多出来的一维用来表示模型中的常数项，建立以下模型。

 

H(theta)可以用向量表示成

那么它的Cost function就是

 

 

        用向量表示成如下：

function J = computeCostMulti(X, y, theta)

	J = 0.5 / m * ((X * theta - y)' * (X * theta - y)); 
end

 

 

        用梯度下降法来求最优值：

 

        用向量可以表示成：

function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
       m = length(y); % number of training examples
       J_history = zeros(num_iters, 1);

       for iter = 1:num_iters
               theta = theta - alpha / m * ((X * theta - y)' * X)';
       end
end

4.  Feature Scaling

        如果theta的数据范围差距很大，需要将这些数据标准化，原因是不标准化可能需要更多次的迭代，影响算法效率。

 

 

 

        Featurescaling的目标是把每一个特征xi变换成在-1到1的范围内，方法有mean normalization：把xi替换成xi-u（u是所有样本的xi的平均值），这样所有的样本就分布在0左右了，然后再除以样本的范围或者样本的标准差

 

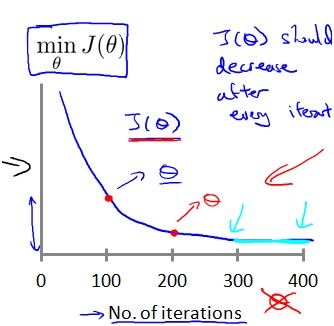
        模型学习的时候，正常情况下，目标函数变化如下

 

        如果alpha太大，则会出现下面的情况

 

5.  多项式回归

        如果把x的特征选取多项式比如x^2,sqrt(x),那么可以拟合成曲线，这里要注意过拟合的问题，另外模型的选取要符合实际情况。