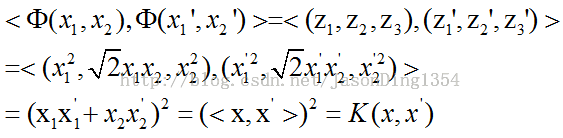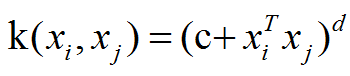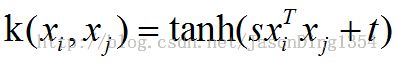【Kernel Method系列】Kernel Method入门
引言:
核方法是20世纪90年代模式识别与机器学习领域兴起的一场技术性革命。其优势在于允许研究者在原始数据对应的高维空间使用线性方法来分析和解决问题,且能有效地规避“ 维数灾难”。在模式识别的特征抽取领域,核方法最具特色之处在于其虽等价于先将原数据通过非线性映射变换到一高维空间后的线性特征抽取手段,但其不需要执行相应的非线性变换,也不需要知道究竟选择何种非线性映射关系。目前,核方法已大量应用到机器学习、模式识别、生物特征识别、生物信息学、数据挖掘、机器学习、图像去噪等领域。
核方法在实际应用中仍然面临大训练集下实现效率低甚至不能实时应用的缺点。一方面,核方法对一个样本进行特征抽取时,需计算该样本与所有训练样本之间的核函数,因此,核方法的特征抽取效率会随着训练样本集的增大而下降。另一方面,核方法作为一类学习方法,依赖和期待利用大训练集来提高方法的泛化性能。这样的特点阻碍了核方法的推广和应用。
1、解决模式识别问题的技术框架
模式识别的目标是依据一个物体的描述数据,区分其所属类别。一个模式识别系统主要包括数据采集、预处理、特征抽取(或特征选择)、分类或匹配等主要步骤。其中,特征抽取主要采用变换的技术实现,在某些情景中,特征选择代替了特征抽取,特征选择一般是从原始数据的所有分量中挑选出若干便于区分各类目标的分量。分类步骤借助于分类器并依据样本的特征抽取结果,识别出一个样本所对应的类别。
1.1 特征抽取与变换技术
特征抽取有两方面作用:一是寻找针对模式的最具鉴别性的描述,以使此类模式的特征能最大程度地区别于彼类;二是在适当的情况下实现模式数据描述的维数压缩。
在特征抽取的众多方法里,其中主流的是基于空间变换的方法。其目标是将原始数据变换到一个新空间,以使在新空间中不同类别间数据有最大分离性,或使新空间中的数据对原数据有最好的描述能力。基于变换特征抽取技术分为线性和非线性两部分,常用的线性变换技术包括主成分分析(PCA)、线性鉴别分析(LDA)等。线性变换技术一般是一种性能较优的降维技术,但其很难根本改变原始数据的线性可分离性。
1.2 非线性变换与特征抽取
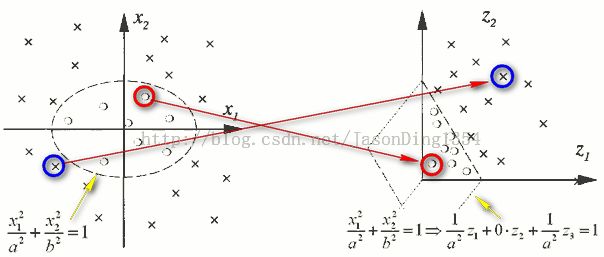
图1 非线性变换
图1显示了原始数据空间到特征空间(feature space)的变换(Φ : R² -> R³ ,即(x1,x2) -> (z1,z2,z3)=(x1²,√2x1x2,x2²)。这样由二维数据转换为三维数据之后,决策边界(decision boundary)由一个椭圆变换成为一个超平面(hyperplane),因此,在特征空间中,问题简化成根据映射的数据去估计线性的分界面(即超平面)的问题。
图2 推导核函数
于是我们可知,该变换用到的是多项式核函数。常用的核函数包括高斯核函数、多项式核函数、sigmoid核函数,其分别定义如下
图3 高斯核函数
图4 多项式核函数
图5 sigmoid核函数
说明:xiTxj用来表示xi,xj均为列向量情况下两者之间的内积。
2、本文小结
理论上讲,核方法可将原样本数据映射到一个非常高甚至无穷维的空间,但是它所对应的特征方程中矩阵的维数仅为训练样本个数;换言之,虽然核方法本质上将数据变换到高维空间,但它不需直接在高维空间中求解;其问题求解空间的维数仅等于其训练样本个数。实际上,这正是核方法作为一种非线性方法能克服维数灾难的关键。
转载请标明出处,原文地址:http://blog.csdn.net/jasonding1354/article/details/36220923
参考文献:
1、模式识别中的核方法及其应用,徐勇 张大鹏 杨健著
2、Learning with Kernels