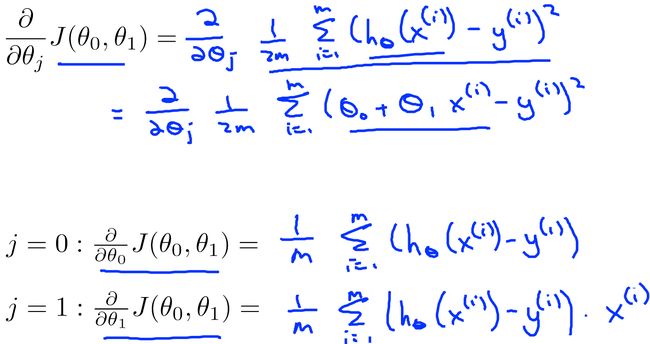斯坦福机器学习公开课笔记(一)--单变量线性回归
公开课地址:https://class.coursera.org/ml-003/class/index
授课老师:Andrew Ng
1、model representation(建立模型)
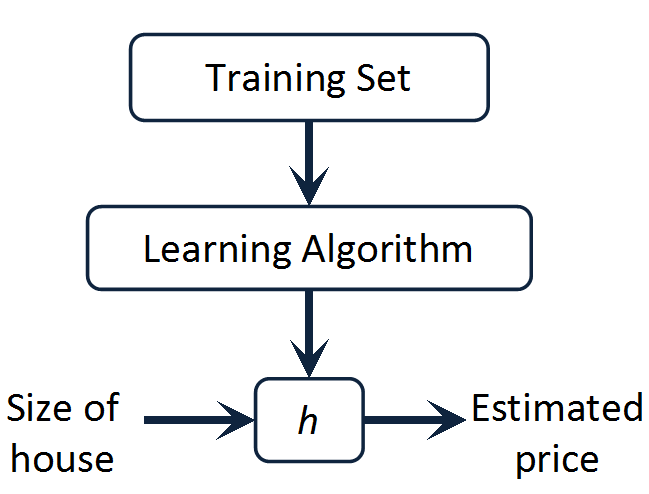
考虑一个问题,如果给定一些房屋售价和房屋面积的数据,现在要预测给定其他面积时的房屋售价,那该怎么办?其实这是一个线性回归问题,给定的数据作为训练样本,用其训练得到一个表示售价和面积关系的模型(其实是一个函数),然后用这个函数进行预测。基本流程如下:
2、cost function(代价函数)
ps:其实这一节中代价函数并未出现代价函数
既然我们已经明确了只需要训练得到一个函数,那我们首先要做的就是对函数的形式进行假设。这里我们可以假设是最简单的线性函数:
下面问题就转变为如何求出theta值。由于我们已经有一些训练数据,虽然不知道数据之间是不是像假设那样成线性关系,但存在一点偏差我们并不介意,只需要让函数值尽可能接近真实值即可。这里我们让x表示面积,y表示售价,在二维平面上描出一系列的点。
3、cost function intuition 1(代价函数初步1)
前面已经说明了需要让h函数值和真实值之间误差尽可能小,这里给出一个更清晰的说明:
代价函数J就代表了上面提到的误差,这里为了后面求导方便函数被写成了这种形式,我们的目标就是让代价函数J值最小,注意在J中theta变成了变量,m代表训练样本的数目(也就是坐标系中点的个数)。
4、cost function intuition 2(代价函数初步2)
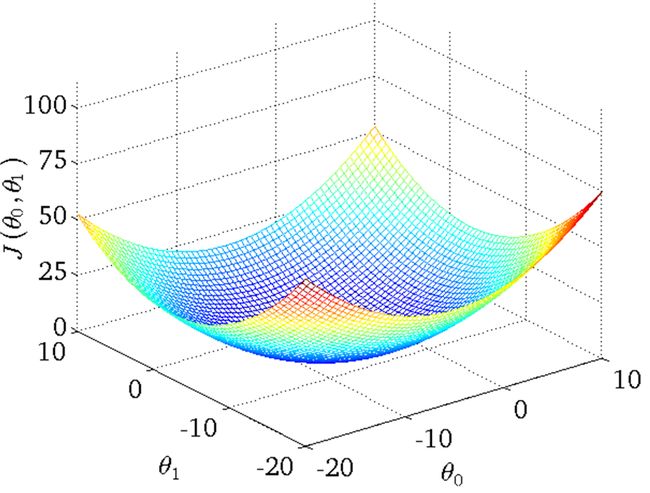
在给定一个theta0和theta1时,我们能找到相应的h函数(一条线)和代价J(一个值),当把这两者放在一起对比观察时,就能清楚的看到代价值在h函数和样本点拟合的很好时是最小的,而且存在全局唯一的最小值。代价函数J用三维表示大概就如下图所示:
从上图可以看出,此时h函数与样本点拟合的情况最好,而代价函数J也取到了最小值,theta0和theta1此时的取值可以从J的横纵坐标上看出。
5、gradient descent(梯度下降)
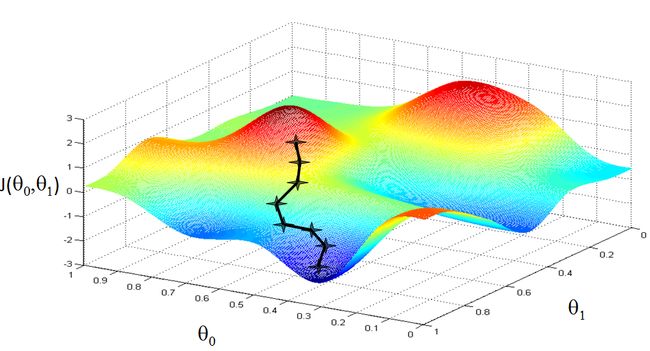
为了让J最小,我们的想法是通过改变theta的取值来改变J的取值。这里对theta的初始值不做要求,只考虑改变时的变化。梯度下降在这里的意思也就是沿着J函数的梯度方向改变theta让J取值减小,形象化的表示如下:
如果懂一点微积分知识,我们就可以把这个下降过程用数学式子像下面这样表达出来:
其中alpha是学习率(大于0),可以理解为每一次下降的步长,需要人为设定。
6、gradient descent intuition(梯度下降初步)
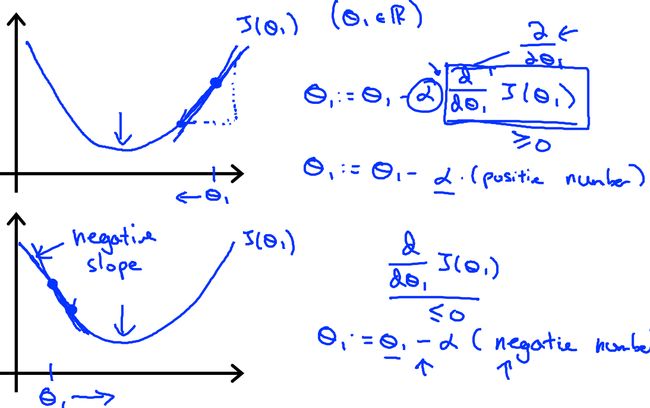
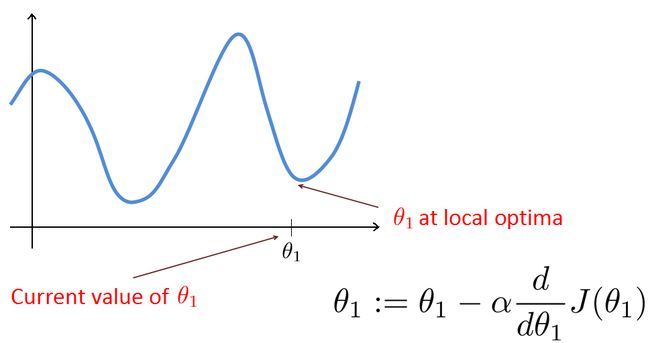
我们可以对上面梯度下降的公式进行一下简单的验证,如下图,当theta值过大时,梯度为正值,每一次迭代theta减小,J值也减小,同理theta值过小时,迭代让theta增大,J值也减小。所以梯度下降的思想是正确的。
相比之下,alpha的选择就不那么简单了,alpha选择要求适中,过大过小都不好:
如上图所说的,alpha取值太小步长太小,要走很多步才能下降到最小值,处理速度太慢。当alpha取值较大时,步长太大,会在最小值左右发生震荡,而永远也达不到最小值。不过,即使alpha取值适中,我们也可能会陷入到局部最小值,达不到全局最小。
补充一点,即使alpha值固定了,在梯度下降的过程中步长也会自动逐渐减小,所以我们不需要在函数逼近最小值的时候减小alpha的取值,以防止步长过大可能会跳过最低点。
7、gradient descent for linear regression(针对线性回归的梯度下降)
针对线性回归,由于我们已经有了代价函数J的形式,只需要代入即可:
写的更好看一点就是这样:
通过迭代,我们就能到达一个J的最小值,这里并不保证是全局最小。
--------------------------------------------弱弱的分割线--------------------------------------------------------------
以上就是第一讲单变量线性回归的内容,思想还是很明确的。首先根据训练数据定义出模型函数形式,通过与真实值求误差得到代价函数,然后通过对代价函数梯度下降确定出模型函数的参数。确定好参数,下面就可以拿这个模型进行预测了,不过由于这里是线性的,变量只有一个,不是很准。自然下面就该引入多变量,非线性的情况了,那个肯定要复杂一些。