Double-Array详解
Trie结构是模式匹配中经常用到的经典结构,在字符串处理中发挥着重要的作用,比如分词算法,就会利用Trie结构将分句的已知词条先识别出来,然后再判断剩下的未识别部分是否是新的未知词。
经典的Trie结构如下图所示,
是一个典型的多叉树结构,为了保证用Trie结构进行模式匹配的效率,Trie结构的每一个节点往往会容纳输入字符集的所有字母构成的数组,以便实现高速查找,这样的缺点就是内存空间的大量浪费,因为越到Trie结构的叶节点,每个节点所包含的字母数量就越少,很可能出现为了几个字符,而多出几十个空位的情况.如上图,没有一个Trie节点的元素多于3个,但是为了算法的效率,每个节点都需要预留26个空位。读者可能会考虑对于Trie结构的每个节点,用散列表代替数组,改直接查找为散列查找,来减少空间的浪费,但是像Trie这样的基本处理工具,每秒钟可能需要对目标文本执行上万次的匹配操作,散列计算的开销很可能会成为影响程序效率的瓶颈。那么有没有既可以充分利用节点空间,又可以避免散列计算开销的Trie实现呢。Jun-Ichi Aoe(日本)于1989年提出的double-array结构,正是将Trie结构的高效率与空间的紧凑利用相结合的理想解决方案。
前面我们提到,可以用散列表来节省Trie结构节点的空间浪费,但是我们又不想对每一次字符查找都进行散列运算,实际上,我们使用散列表的初衷,无非也就是对于当前节点,我们去哪几个节点去匹配下一个输入字符。这里我们以字符集a-z为例,来考虑如何实现Trie结构的压缩存储。
如上图所示,我们假设有一个很长的数组BASE[1...n],此时对于集合K,我们可以将BASE[1...26],作为对应的Trie结构的根节点,这样对于第1个输入字符,肯定可以映射到BASE[1...26]中的一个,然后我们将BASE[27...52]作为当第1个输入字符是a时,第2个字符对应的区间。BASE[53...78]作为当第1个字符是b时,第2个字符的映射区间,依次下去,将BASE[27...702]对应Trie结构根节点26个字母所分别对应的的第2层顶点。此时我们实现了将Trie结构的各层顶点映射到一个一维数组上面。为了能够索引到对应的BASE数组中的正确位置,我们还需要一个CHECK数组与BASE中的元素一一对应,来标记当前字符是从哪个父节点索引过来的。比如说BASE[53]的a是从BASE[2]=b索引过来的,而不是从BASE[1]或者BASE[3]索引过来的,对应于模式串前缀ba,而不是aa,ca。以上图为例,CHECK[27]到CHECK[52]的值都等于1,说明节点1是节点27-52的父节点。对于当前节点i,输入字符c,BASE与CHECK的关系是CHECK[BASE[i]+c]=i。
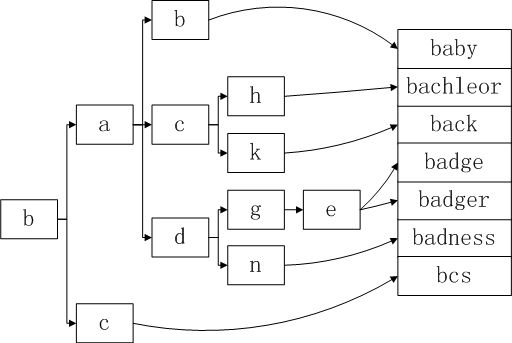
下面我们来看一下如何利用这种形式的Trie结构,并根据输入的模式集合,来充分利用内存空间。对于输入集合K={baby,bachelor,back,badge,badger,badness,bcs},我们会发现其对应的Trie结构的根节点只有一个合法输入b,也就是说BASE[1...26],我们只用到了一个节点BASE[2],其余25个节点都白白浪费掉了,那么我们有没有办法把这些地方复用为Trie结构的2层节点呢。字母b之后的合法输入有a,c,所以我们可以考虑找到这样的一个位置r,使得BASE[r]+a,BASE[r]+c都是还未使用的节点,这样我们就可以把r作为父节点b的2层子节点的索引位置,容易得到r=1,就满足条件,所以,我们没必要使用BASE[27...52]的空间来存放b的子节点a,c,直接使用BASE[1],BASE[3]就可以了。此时BASE[2]=0,CHECK[1]=CHECK[3]=2。同样,对于输入ba其后的合法输入有b,c,d三个,我们可以找到一个位置r令BASE[r]+b,BASE[r]+c,BASE[r]+d都为未使用节点,然后将ba之后的子节点安排在这几个位置就可以了。r=2就满足条件,此时BASE[1]=3,CHECK[3]=CHECK[4]=CHECK[5]=1。
下面给出对于模式集合K构建Double-Array的算法。
我们以例子来说明Double-Array的构建算法。模式集合K={baby,bachelor,back,badge,badger,badness,bcs},输入字符集合a-z对应数字0-25,BASE,CHECK数组均从0开始,所有单元的初始状态都为-1。另外对于BASE数组中的值,我们需要分区使用,后面会解释。这里首先要说一下独立后缀的概念,以模式集合K中的模式badness为例,其前缀b,ba,bad分别都与其他模式的前缀有重叠,而前缀badn就是模式badness的独有前缀了,所以从n到模式末尾的整个后缀ness,就是模式badness的独立后缀。对于模式串的独立后缀,我们无需将其组织在Trie结构中,而专门将其甩到另外一个结构TAIL中集中管理。
1 2 3 4 5 6 7 8 9
b a b y
b a c h e l o r
b a c k
b a d g e
b a d g e r
b a d n e s s
b c s
现在我们分层来构建集合K的Double-Array Trie结构,首先我们考察集合的第1层(也相当于所有模式串的首字母)所构成的集合S1,我们发现S1={b},此时我们在BASE数组中要找到这样的位置i对于S1的所有元素s,有BASE[i+s]=-1。对于集合S1,我们发现i=0有BASE[0+1]=BASE[1]=-1就满足条件,所以我们将CHECK[1]=-1保持不变。
接着我们来处理集合的第2层。在之后的处理中我们要注意,只有前缀相同的一组字符,我们才把他们作为一个集合来处理,相当于Trie结构的一个节点。对于本例来说,所有模式串的第1个字母都是b,我们可以得到一个集合S2={a,c},我们需要在BASE中寻找i使得BASE[i+0]=-1,BASE[i+2]=-1,此时0满足条件,我们对于集合S2的共同前缀b,找到其在BASE中对应的位置是BASE[1],所以我们令BASE[1]=0,CHECK[0]=CHECK[2]=1。这里对于满足条件的i值,我们只取满足条件的正值,但是不一定是最小的。
再接着处理第3层,此时前缀ba的直接后继字母集合S3={b,c,d},我们发现i=2可以满足BASE[3]=BASE[4]=BASE[5]=-1,此时我们用前缀ba找到其在BASE中的位置BASE[0],令BASE[0]=2,同时令CHECK[3]=CHECK[4]=CHECK[5]=0。而前缀bc的直接后继字母集合S4={s},这里我们不会将s安置在BASE数组中,因为前缀为bc的模式串只有一个bcs,所以对于模式bcs来说,前缀bc之后的部分已经形成了前面所说的独立后缀,也就是说当匹配完前缀bc之后,后面的匹配就由多模式匹配退化为目标串的与bcs的后缀s的匹配操作,此时就不需要再用Trie结构来进行查找,而直接将目标串的余下部分与s执行比较就可以了。所以我们让TAIL[1]="s"。
用上面的办法逐层处理模式集合的字符,按照公共前缀分组处理(例如公共前缀bad的后继集合S4={g,n}),遇到独立后缀,就将该独立后缀加入TAIL数组中,直到把所有模式串的独立后缀都加入到TAIL表中为止,构建Double-Array结构完毕。这里有一种情况需要特别关注,以模式badge和badger为例,badge是badger的包含前缀,当我们构建到badge尾部的时候就会出现既要索引TAIL表中的对应独立后缀(此时TAIL表的独立后缀为空串,但是依然要有),以表示一个匹配模式被发现。又要继续跳转的双重需要,此时我们可能需要对BASE值进行分区使用来兼顾这样的需求,比如将BASE值分为高16位和低16位,高16位用于索引TAIL数组,低16位用于实现跳转,当BASE值大于65535时,说明当前BASE值索引到了一个匹配模式的独立后缀,将其减去65535,所剩下的就是对应的TAIL索引。AOE的论文中是在每个模式的后面加入一个不可能字符使得任何两个模式都不存在前缀包含关系,来解决这个问题的。
上面就是逐层构建Double-Array的基本步骤,用此方法构建的Double-Array结构如图所示,由于BASE中的数值可能包含多重意思,这里将可以直接索引的模式,直接写在BASE的对应单元内,当匹配到达这些单元时,直接将输入的字符与后缀进行比较即可:
利用构建好的Double-Array匹配指定的模式的算法步骤如下。将临时变量r置为0,对于首位输入字符c,我们先要判断BASE[c]和CHECK[c],如果BASE[c]!=-1,CHECK[c]=-1,则令r=c,继续执行后续的匹配查找。如果不匹配,说明输入字母c不是Trie结构的根节点成员,放弃之。然后我们得到t= BASE[r]+c,以及CHECK[t],判断CHECK[t]是否等于r,如果不相等,则说明当前Trie节点不包含输入字母c,在模式集合中中没有该模式,所以匹配失败,否则令r=t,再继续执行上述操作。直到匹配失败,或者最终索引到TAIL中的匹配模式为止。
用上述的方法匹配模式badge的过程如下。
1)对于字母b,BASE[1]!=-1, CHECK[1]=-1,可以继续执行匹配操作, r = 1。
2)对于字母a,t=BASE[1]+a=0, CHECK[t]=CHECK[0]=1, CHECK[t]=r, r=t=0;
3)对于字母d,t=BASE[0]+d=5, CHECK[5]=0, CHECK[t]=r, r=5;
4)对于字母g,t=BASE[5]+g=6, CHECK[6]=5, CHECK[t]=r, r=6;
5)对于字母e,t=BASE[6]+e=8, CHECK[8]=badge,发现匹配。
模式ada的失败匹配过程如下
1)对于字母a,BASE[0]=2!=-1,CHECK[0]=1!=-1,所以ada不是集合中的模式,匹配终止。
模式baec的失败匹配过程如下
1)对于字母b,BASE[1]!=-1, CHECK[1]=-1,可以继续执行匹配操作, r = 1。
2)对于字母a,t=BASE[1]+a=0, CHECK[t]=CHECK[0]=1, CHECK[t]=r, r=t=0;
3)对于字母e,t=BASE[0]+e=6,CHECK[t]=CHECK[6]=5!=0,匹配失败,所以baec不是集合中的模式。
后记:
一般的算法或者数据结构,往往是时间和空间的某种妥协,如果要提高运行效率,往往需要一些额外的内存空间,反之亦然。而Double-Array之于Trie结构,就好像是一种完美的诠释,在实现了对Trie结构空间的充分利用的同时,又不牺牲查找速度,那么是不是Double-Array就无懈可击了呢。当然不是。要驾驭这种优美结构的代价,就是实现Double-Array的高复杂性,以及在Double-Array中插入,修改,删除单条数据的高代价。AOE在论文中详细介绍了Double-Array的增加,变更,删除条目的操作算法,相较于通俗的Trie实现,要复杂的多得多,本文我也仅仅是将自己对Double-Array的一点浅显理解写出来而已,实际上Double-Array是一个相当复杂的数据结构,他只能在某些应用场合替代普通的Trie结构,以后如果条件允许,我还会将Double-Array的更多细节一一介绍。