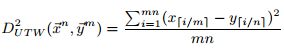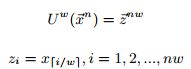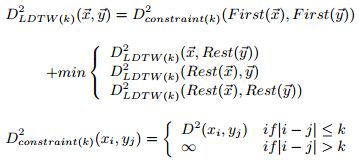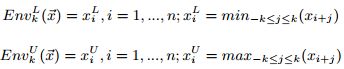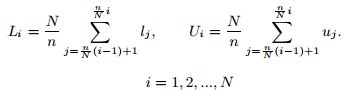Warping indexes with envelope transforms for query by humming
本文是哼唱检索早期的经典论文,只翻译其核心的系统体系结构,DTW及其变形,结论三章,全文参见https://cs1.cs.nyu.edu/cs/faculty/shasha/papers/humming.pdf
首次翻译论文,术语若有错误请指正哈
概述:将音乐和哼唱分成时间片,用包络变换改进DTW
一、系统体系结构
系统分为3部分:输出的哼唱查询,音乐库,用于高效查询的音乐库索引
1、用户哼唱:输出的哼唱查询
单声道,输入转化为帧,帧长10ms,用音高追踪算法从帧中提取音高,生成音高时间片段,一般人想要哼出精确的音符边界很难,所以本文不考虑音符分隔
2、音乐数据库
数据库为音乐旋律的集合,旋律由一个元组序列表示,元组即(音符,持续时间),不考虑音符之间的空余时间和静音时间的信息,将元组转化为一维序列,即音符持续多少帧,就重复多少次,即由(Ni,di) -> Ni,Ni,...Ni (持续di次)
由于用户哼唱的是旋律的一部分,所以系统要支持子旋律匹配,两种方法:
(1)子序列匹配:子序列查询一般比整体序列查询慢,因为候选序列太多了
(2)整体序列匹配:将每段查询分成若干片段,用哼唱查询去匹配数据库里每一个旋律分片
所以使用整体序列匹配
3、建立数据库索引,用于高效查询
大多数人哼的不完全正确,如节奏会有变化,系统做如下处理:
(1)绝对音高:哼唱的绝对音高不恒定,对音高做减均值处理
(2)节奏:哼唱节奏可能是原来的0.5-2倍,并认为是线性变化,做线性缩放(或者称为均匀时间规整)
(3)相关音高:假设哼唱的和原来旋律每个音符持续长度相同(能完全对齐),而在对应的时间片上音高不同,所以哼唱和候选的距离可以用每个时间片每个音符的音高差的和表示,距离越小,哼唱和候选越相似。找最相似片段就是最近邻查询。
(4)局部时间变化:每个哼唱音符的持续时间不完全正确,用动态时间规整(DTW),允许匹配时每个音符的节奏变化。主要思想是,局部拉伸压缩时间轴,最小化两个时间片的点到点距离。本文最大亮点在于提供一种DTW的高效索引方案
归根结底,就是要把两个时间片调整到具有相同的绝对音高和节奏(规范化),才能比较距离
但是顺序遍历所有时间片耗时太大,需要降维并建立索引
降维方法:GEMINI框架,给出降维转移矩阵,将时间片向量做降维变换,降维后的向量称为之前时间片的特征向量,可以用R*树或者grid file建立索引。为了保证没有负值,变换后的曲线必须是原来的下界
常用的降维变换:傅里叶,小波,SVD,PAA(Piecewise Aggregate Approximation)
本文扩展GEMINI框架以适用于DTW
二、动态时间规整DTW
用到的符号:
距离测度:欧氏距离
D(A,B) = sqrt [ ∑( ( a[i] - b[i] )^2 ) ] (i = 1,2,…,n)
定义1:两个向量x,y之间的DTW距离定义为:
计算DTW距离可以形象的看成用动态规划匹配字符串。
建立一个n×m的矩阵,用于对齐两个时间片![]() 和
和![]() ,矩阵的元素(i,j)表示
,矩阵的元素(i,j)表示![]() 和
和![]() 对齐,对齐的过程就是选择一条从(1,1)到(n,m)的路径P,是两个向量之间的欧氏距离最小。
对齐,对齐的过程就是选择一条从(1,1)到(n,m)的路径P,是两个向量之间的欧氏距离最小。
![]() 是
是![]() 和
和![]() 在对齐时的位置标号,两个向量的距离就是
在对齐时的位置标号,两个向量的距离就是![]() 和
和![]() 之间的距离,对路径P的约束是:
之间的距离,对路径P的约束是:
(1) 单调性:![]()
(2) 连续性:![]()
可能的规整路径P的数量随着向量长度的增加以指数形式增加,最短的路径即为DTW路径,这个问题的解可以用动态规划方法求出,时间复杂度O(mn)。
1、 统一时间规整UTW
UTW是DTW的一个特例,对路径P的约束:必须是对角线(路径不能拐直角弯)
定义2:两个向量![]() 和
和![]() 之间的UTW距离定义为:
之间的UTW距离定义为:
为了简化符号,将x,y的长度都扩展为mn。如果他n和m的最大公约数GCD(n,m)大于1,那么长度就扩展为他们的最小公倍数LCM(n,m)。
用升采样的概念,UTW的定义可以被简化。
定义3:对![]() 的w倍升采样可以定义为:
的w倍升采样可以定义为:
直观来看,w倍升采样把每个值重复了w次,下述引理把UTW距离缩小至欧氏距离。
引理1:
UTW是时间缩放的一般化。在时间缩放中,一个时间片的长度必须是另一个长度的整数倍,在UTW中没有这个约束。通过UTW,可以计算不同长度的时间片的距离。![]() 的UTW范式为
的UTW范式为![]() ,nw是一个预定义的大整数,可以方便的计算出一个时间片的UTW范式。
,nw是一个预定义的大整数,可以方便的计算出一个时间片的UTW范式。
2、 局部动态时间规整LDTW
UTW的约束太过严格,可以用LDTW来放宽约束。直观来讲,人们一般会通过如下方法匹配长度不同的两个时间段:首先,将两个时间片全局扩展为相同的长度;然后,进行局部的点对点比较,伴随时间轴上的小幅调整。这样一个两部的变换在避免一些不直观的结果和提高速度的基础上,可以用传统DTW仿真。下面是LDTW的定义。
定义4:向量x,y的k-LDTW距离定义为:
上式直观理解就是,规整时对齐的x,y坐标差值不大于k。
下面的网格图展示了k=2时LDTW的规整路径P。
规整宽度定义为:![]() ,意义就是规整路径的最宽处与总长度的比值,这种约束被称为Sakoe-Chiba带。运用动态规划计算k-LDTW的时间复杂度是O(kn)。
,意义就是规整路径的最宽处与总长度的比值,这种约束被称为Sakoe-Chiba带。运用动态规划计算k-LDTW的时间复杂度是O(kn)。
结合DTW和LDTW,定义更通用的DTW距离。
定义5:两个时间片的DTW距离就是它们UTW范式的LDTW距离
换句话说,DTW距离就是两个时间片升采样到相同长度后的LDTW距离。下文中将不区分LDTW和DTW,并且认为LDTW就是两个时间片的UTW范式计算出来的。
3、 下边界技术和建立索引策略
LDTW可以确定局部距离的下界,比DTW的全局下界更精确,误报更少。
为了简化符号,先介绍几个时间片包络的概念。
定义6:长度为n的向量x的k-包络为:
![]()
等式右边两个参数分别代表x的上下界,即包络。
包络为当前点i加减k范围内的上下界。
定义7:时间片x和包络e的距离定义为:
![]()
其中,z定义为:![]() ,即z可以取上下界范围内的任意值。
,即z可以取上下界范围内的任意值。
引理2:
![]()
即时间片x和另一个时间片y的包络的距离是x,y的DTW距离的下界。
为了在GEMINI框架中建立时间片索引,需要对时间片和包络做降维变换。使用段聚集近似(PAA)的方法。设![]() 的PAA变换是
的PAA变换是![]() ,N<<n,则:
,N<<n,则:
即,将原来n维的向量x降为N维,就是分成n/N段,每段取平均值。
对于包络![]() 的Keogh-PAA降维变换
的Keogh-PAA降维变换![]() 为:
为:
即,下界的PAA结果为每段的最小值,上届的PAA结果为每段的最大值。可见包络的PAA实际上是一个分段常函数,确定包络边界,但不交叉。
本文定义一种新的包络PAA降维方法:
上式同样是一个分段常函数,但是上下界计算的是每段上下界的平均值。
下图显示了用上述两种PAA方法计算的包络,可见用新PAA计算的上下界更精确,并可看出对任意时间片都适用。本文会证明新的边界同样可以保证真实DTW距离的下界。
证明本文的PAA变换能保证DTW下界之前,先讨论一般的包络降维变换在DTW距离下如何建立时间片索引。这是本文的要点。定义一个包络降维变换的容器性质如下。
定义8:称对于包络e的变换T是“容器不变的”,如果满足条件:
![]()
就如时间片的变换是下界,能保证在欧氏距离下无漏报,包络变换是容器不变的,能保证在DTW距离下无漏报。
定理1:如果变换T是容器不变且有下界的,那么:
![]()
即,x的变换和y包络的变换的距离是x,y的DTW距离的下界
定理1证明:
根据容器不变的概念,可以依据PAA,DWT,SVD,DFT设计包络变换。所有这些降维变换都是线性变换,因为:
可以扩展这些用于时间片的变换为用于时间片包络的变换,同时保证变换是容器不变的。
引理3:令变换T是一个线性变换,即满足上式,对包络e的T变换如下:
其中t为符号函数:
上述变换的意义:若变换T的参数aij是正的,那么上下界也按照和x相同的方式变换,若aij是负的,那么上下界要互换。
所以变换T是容器不变的
证明:
包络的变换还是一个包络,称为特征空间的包络。特别的,当包络和时间片相同时,那么包络变换就是时间片的变换。由于PAA是一个线性变换,所以由上述引理推出的包络PAA变换是容器不变的。PAA还有一个不同于DFT或SVD的优点,就是所有变换的系数都是整数。在这个条件下,特征空间中的上界就是上界的PAA变换,下界同理。对DFT和SVD变换来说,特征空间的上界是上下界组合的变换。所以,PAA特征空间的包络比DFT和SVD的总体上要精确。
使用DTW的时间片数据库查询策略:
一个t-范围近似查询是查找数据库中与查询距离小于t的时间片,包括以下步骤:
1) 对时间片![]() 计算其特征向量
计算其特征向量![]()
2) 在![]() 上建立N维的索引结构
上建立N维的索引结构
3) 对一个查询![]() ,计算包络
,计算包络![]() 和包络变换
和包络变换![]()
4) 在索引结构中,对![]() 做一个t-范围的查询,返回时间片集合S
做一个t-范围的查询,返回时间片集合S
5) 计算S中时间片和查询![]() 的真实DTW距离,滤除误报。根据定理1,可以保证无漏报
的真实DTW距离,滤除误报。根据定理1,可以保证无漏报
类似的,可以在这样一个范围查询上建立一个k-最近邻查询,使用DFT, DWT, PAA, SVD等方法对时间片数据库建立索引,并可以在不重建索引下加入DTW。可以这样做,是因为本文的框架支持所有线性变换,并且添加DTW仅需要时间片查询的变化。
三、结论
本文提供一种使用DTW建立时间片数据库索引的改进方法。改进之处在于时间片包络的降维变换。给出一种普遍方法,来调整欧氏距离测度下的时间片索引策略,以适应DTW距离测度。可以保证在包络降维变换是容器不变的情况下,这种索引策略没有漏报。用这个方法,本文提出的对DTW的PAA变换比原来的PAA变换普遍要好。
基于时间调整索引,时间片数据库对哼唱检索有很高的精确度,速度快且可扩展。用本文提出的方法初步实现一个哼唱检索系统,真人测试效果令人满意。系统依然不成熟,还在扩充数据库并使系统适用于不同的哼唱者。然而,该系统在娱乐和教育领域有巨大潜力。