从GRE数学题说起

又是好久没有认真写博客了，一天忙成狗了快，时间就仿佛内存一样全成了碎片，连续这个条件对于我来说真的是太苛刻。上周日上了GRE课程中唯一的一次数学课，老师是鄙校化学系的，当初怀着科学梦想，最后不得不去了XDF（原因我想肯定不像他说的那么简单的）。大家都说GRE数学对于中国学生来说很简单，你不考个满分都不好意思自己是中国人。但是，我从这些题目中，感受到的却是一种思维训练和从实际应用出发的基本原则，不像..(还是省略掉吧)。比如：Party问题和正太分布(68%,98%)问题等。说起国外的题目，就拿通信来说，由于有许多出国的同学，我也有机会接触到他们的平时作业，感觉与国内就是两种风格的问题。不管美帝还是欧洲，大多题目一看，你第一反应是：嗯，这个问题值得考虑，有价值。接下来，你会发现这个问题思维量不像你想的那么简单。更重要的是，国外的老师更强调用数学表达式来表达一个语言很容易描述清楚的东西，我想这点在编程方面是尤为重要的吧。反观之，这边的作业就是几个随机过程，几个X，几个Y，翻来覆去折腾来折腾去，我反正是深深地被折磨了，以至于我很痛快地把它们一口气都弄完（感谢Mathematic~），然后眼不见心不烦地坐下来写博客了。今天就从GRE课上老师举出的一个趣题开始说起吧。

题1：n只鸡，排成一列，编上号，从一号开始，每隔一个开始杀（到最后返回从2号开始继续），问最后剩下那只鸡的编号？

注：如果觉得这个题目太中国化，我觉得有必要变化下，那就有点类似我们经典的Josephus问题了。改后：现在岛上总共有n外来人，酋长叫你们这n个外来人站成一列，他从第一个开始杀（这是不是就刺激了？哈哈~），请问你要站在哪个位置，才能坚持到最后？

解：对于这个问题，相对来说就是小学奥数低年级奥数的水准吧（我自己的数学一向很烂，所以没资格谈太多。）既然我是学了递归的人（就好比有了计算器还非得手算，我觉得有点二了。），我就不用小学生的办法来解这个问题了。大致如下：

1 2 3 4 5 6 7 8 9 10

2 4 6 8 10(1次后)

4 8（2次后）

8（最后）

我们另J(n)表示这个问题的解，也就是n个人时最后那个人的编号。我们会发现:当我们杀一遍后，数目减半(奇数时，n-1/2，不影响递归，可以认为也是减半)，例如n=10,一遍后n' = 5,然后我们的问题跟刚才一样，只是规模减半了（在参考文献[1]中，就是说这种递归很给力，当然dichotomy的威力就在这）那么，我们需要做的就是确定J(n')等于多少，我们易只J(5)=2,也就是排在第二那个位置上的人，能活在最后。而我们现在这个5个人中，第二个位置上的人，他的编号是2*2=4,第i个位置上的人他最初的编号为2*i。总结一下：就是每次减半，位置与编号的关系就要乘以2，当最后减半到只剩一人时，J(1)=1。那么我们就可以知道J(n)=2^k，其中k 即为把n长线段二分到1所需要的次数。简单说J(n)就等于n内最大的2的整数次幂。例如n=10时，最大为2^3=8，也就意味着长度为10的线段二分到长度1，最少次数为3，这也就是常见的二分查找O(logN)的来源。

好了，我们现在就可以很快知道如下结果了J(15)=8,J(30)=16 当然满足J(30)=2*J(15)。

其实，今天的重点是二进制，我们用二进制的思想来解释二分的思想吧。例如n=10，我们表示为二进制(1010)，它减半为(101)就是右移一位对不？这个很简单。对于奇数的n=2m+1=11，它的二进制(1011)，它减半为多少呢？按照题意，每次杀一遍后，我们剩下的是m=(n-1)/2，m的二进制表示仍然为(101)，所以不管奇数还是偶数，我们只要右移一位就行，那我们就看最高位的1需要几次移动到最低位就行啦。

题2：我们把题1的列变成环，n个人站成一个环，其他条件不变，问最后剩下那个人的编号。注：当然【参考文献1】里的题目是从2号开始杀的，然后也是用递归解，只不过此时奇数偶数不再相同，思想类似。这个题也是许多投行金融面试笔试必考题吧，至少我听了不下n个人说过了。

我们易知，当n=2k时，J(n)=2J(n/2)，(思想类似于题1)。所以当n=2^m时，J(n)=n。   当n=2^m+a时，同题1一样，我们把n表示为最大2的整数幂 + 一部分的形式。

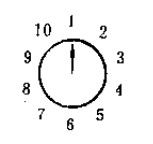
引用来自[参考文献1]中的一个十分巧妙的思想来解这题：我们由上面推理，知道当n=2^m时，剩下的就是最后一个。那么n=2^m+a 经过a次屠杀后（注意：是杀a个人或者鸡后），n' = 2^m，我们把“尸体收拾干净”，也即重新整理这个环，此时最后一个元素就肯定是最后剩下的了。那么杀了a个人（隔一个杀一个）后，新的第一个人是编号多少呢? 如图所示，我们杀掉1号和3号后，剩下8个人，刚好为2的整数次幂。此时新的第一个人为5=2*2+1，新的最后一个人（即最后剩下那个人）编号4=2*2。所以我们知道，对于任意n=2^m+a，经过a次杀戮后，最后那个人的编号为2*a，即便得到如下式子：

J(2^m+a)=2*a ，其中2^m是n 内最大2的整数幂。所以J(10)=(10-2^3)*2=4,J(15)=(15-2^3)*2=14,J(30)=(30-2^4)*2=28 

题3,：就请大家直接参考67大神最新一篇博文吧，也就是关于01二进制问题的。

虫子问题

题4：最后我解答下一个同学关于Shannon-Fano-Elias coding无前缀码的证明问题。

解：其实基本思想还是如这篇博文的理解一样：无前缀码的理解，我们把码字表示为二进制，它就代表一个区间，区间的长度为2^(-L)，只要证明码字之间不交就行了。具体证明见参考文献2，思路比方法重要。

后记：写到后面有点急，突然又收到一大堆邮件要处理，真的伤不起啊！对不住各位了。

参考文献：

   【1】具体数学：计算机科学基础/(美)格雷厄姆(Graham,R.L.)著.-北京：机械工业出版社，2002.8

   【2】http://www.icg.isy.liu.se/courses/tsbk08/lect5b.pdf

(完)