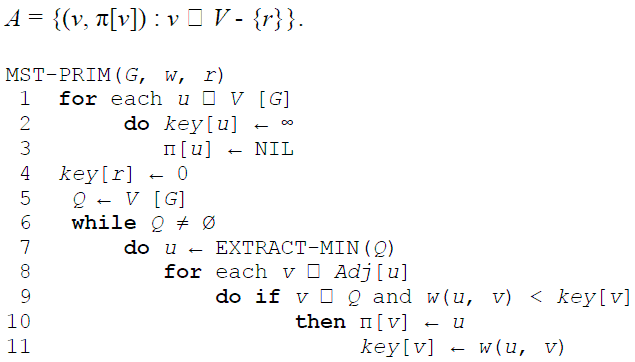算法导论 第23章 最小生成树
一、综述
1.minimum-spanning-tree problem
2.Kruskal's algorithm
In Kruskal's algorithm, the set A is a forest. The safe edge added to A is always a least-weight edge in the graph that connects two distinct components.
3.Prim's algorithm
In Prim's algorithm, the set A forms a single tree. The safe edge added to A is always a least-weight edge connecting the tree to a vertex not in the tree.
二、程序
1.Kruskal算法
#include <iostream>
#include <algorithm>
#include "UnionFindSet.h"
using namespace std;
#define N 14
#define M 9
//边
struct Edge
{
int start;//起点
int end;//终点
int len;//长度
};
//用于排序
bool cmp(Edge a, Edge b)
{
return a.len < b.len;
}
Edge e[N+1];
//Kruskal算法
void Mst_Kruskal()
{
//使用不相交集合数据结构为每个顶点创建一个集合
UFS ufs(M);
//根据可权值的非递减排序
sort(e+1, e+N+1, cmp);
//检查每条边
for(i = 1; i <= N; i++)
{
int u = e[i].start, v = e[i].end, l = e[i].len;
//端点u,v是否属于同一棵树,如果形成一个回路,则放弃
//若不属于同一棵树
if(ufs.Find(u) != ufs.Find(v))
{
//把边加入到集合中
cout<<u<<' '<<v<<' '<<l<<endl;
//对两棵树的顶点进行合并
ufs.Union(u, v);
}
}
}
/*
1 2 4
1 8 8
2 3 8
2 8 11
3 4 7
3 9 2
3 6 4
4 5 9
4 6 14
5 6 10
6 7 2
7 9 6
7 8 1
8 9 7
*/
int main()
{
int i;
for(i = 1; i <= N; i++)
cin>>e[i].start>>e[i].end>>e[i].len;
cout<<"MST:"<<endl;
Mst_Kruskal();
return 0;
}
2.prim算法
使用斐波那契堆的prim算法的程序还是没有实现,原因如下:把所有顶点作为一个斐波那契堆,以顶点的key[v]作为斐波那契堆的关键字。算法过程中会动态地修改key[v]不断变小。斐波那契堆的缺点是查找操作不方便,因此在执行Fib_Heap_Decrease_Key操作时,给的参数是指顶点所对应的斐波那契结点的地址,而不是先给顶点再搜索这个结点。为了得到顶点所对应的斐波那契结点,本文所采用的方法是给每个顶点加一个指向其对应斐波那契结点。然而在Consolidate过程中,会出现 swap(x, y);,即两个结点交换。那么顶点所指向斐波那契堆结点可能就不是顶点所对应的斐波那契结点了。
对于这个问题当然有解决方法,就是修改Binomial_Heap_Decrease_Key操作,不是只交换内容,而且是全部交换。因为斐波那契结点的指针很多,而且这种交换又大量存在,这种解决方法不是一个好方法。
先把写了一部分的帖出来,待以后想到了好方法再改进。
(1)Fib_Heap.h
这个头文件没有修改,见算法导论 第20章 斐波那契堆
(2)Mat_Graph.h
加了一个成为变量node* data[N+1];
#include <iostream>
using namespace std;
#define N 100
class Mat_Graph
{
public:
int n;
int Map[N+1][N+1];
int p[N+1];//π[v] names the parent of v in the tree
int key[N+1];//key[v] is the minimum weight of any edge connecting v to a vertex in the tree
node* data[N+1];
Mat_Graph(int num):n(num)
{
memset(Map, 0, sizeof(Map));
}
void AddDoubleEdge(int a, int b, int value = 1)
{
AddSingleEdge(a, b, value);
AddSingleEdge(b, a, value);
}
void AddSingleEdge(int start, int end, int value = 1)
{
Map[start][end] = value;
}
void DeleteDoubleEdge(int a, int b)
{
DeleteSingleEdge(a, b);
DeleteSingleEdge(b, a);
}
void DeleteSingleEdge(int start, int end)
{
Map[start][end] = 0;
}
void SingleInput();
void DoubleInput();
//22.1-2
void Print();
};
void Mat_Graph::Print()
{
int i, j;
for(i = 1; i <= n; i++)
{
for(j = 1; j <= n; j++)
cout<<Map[i][j]<<' ';
cout<<endl;
}
}
void Mat_Graph::SingleInput()
{
cout<<"输入边的数量"<<endl;
int m, a, b, c;
cin>>m;
while(m--)
{
cin>>a>>b>>c;
AddSingleEdge(a, b, c);
}
}
void Mat_Graph::DoubleInput()
{
cout<<"输入边的数量"<<endl;
int m, a, b, c;
cin>>m;
while(m--)
{
cin>>a>>b>>c;
AddDoubleEdge(a, b, c);
}
}
(3)main.cpp
#include <iostream>
using namespace std;
#include "Fib_Heap.h"
#include "Map_Graph.h"
int n, m;//点的个数,边的个数
void GetVertex(Mat_Graph *G, Fib_Heap *Q)
{
int i;
for(i = 1; i <= n; i++)
{
node *x = new node(G->key[i], Q->nil);
x->data = i;
G->data[i] = x;
Q->Fib_Heap_Insert(x);
}
}
void Mst_Prim(Mat_Graph *G, int r)
{
cout<<"result"<<endl;
int i;
for(i = 1; i <= n; i++)
{
G->key[i] = 0x7fffffff;
G->p[i] = -1;
}
G->key[r] = 0;
Fib_Heap *Q = new Fib_Heap;
Q->Make_Fib_Heap();
GetVertex(G, Q);
while(!Q->IsEmpty())
{
int u, v;
u = Q->Fib_Heap_Minimum()->data;
if(G->p[u] > 0)
cout<<G->p[u]<<' '<<u<<' '<<G->Map[G->p[u]][u]<<endl;
Q->Fib_Heap_Extract_Min();
for(v = 1; v <= n; v++)
{
if(G->Map[u][v] > 0 && G->Map[u][v] < G->key[v])
{
G->p[v] = u;
G->key[v] = G->Map[u][v];
Q->Fib_Heap_Decrease_Key(G->data[v], G->key[v]);
}
}
}
}
/*
9 14
1 2 4
1 8 8
2 3 8
2 8 11
3 4 7
3 9 2
3 6 4
4 5 9
4 6 14
5 6 10
6 7 2
7 9 6
7 8 1
8 9 7
*/
int main()
{
while(cin>>n)
{
Mat_Graph *G = new Mat_Graph(n);
G->DoubleInput();
Mst_Prim(G, 1);
}
return 0;
}
三、练习
23.1Growing a minimum spanning tree
23.1-2
没有找到关于light edge的定义
23.1-3